Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Практичне заняття 7-8.

Тема заняття.Застосування похідної до розв’язування прикладних задач на знаходження найбільшого (найменшого) значень функції.

Теоретичний матеріал.

Під прикладними задачами розуміють задачі, що виникають за межами математики, але розв’язуються з використанням математичного апарату.

Необхідно зазначити, що процесу розв’язування прикладних задач властиві всі етапи математичного моделювання.

В узагальненому вигляді це:

- переклад задачі з природної мови тієї галузі, де вона виникла, на мову математики (I етап, створення математичної моделі);

- розв’язування отриманої математичної задачі (II етап, дослідження математичної моделі);

- інтерпретація отриманих результатів, тобто переклад розв’язку математичної задачі з мови математики на мову тієї галузі, де вона виникла (III етап, інтерпретація розв’язків).

Прикладні задачі на знаходження найбільших і найменших значень реальних величин відносяться до одновимірних задач оптимізації в яких цільова функція є функцією однієї змінної.

Серед методів розв’язування задач на знаходження найбільшого і найменшого значень функції виділяють загальний метод – метод диференціального числення. Цей метод застосовується у випадку, коли цільову функцію 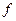вдається отримати у вигляді явної формули типу 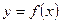і при цьому функція 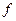задовольняє певні додаткові умови, а саме : 1) функція 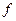визначена і неперервна на відрізку 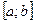; 2) функція 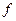диференційована (має похідну) в інтервалі , за винятком можливо, скінченного числа точок; 3) функція 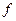має скінченне число точок в яких похідна дорівнює нулю (якщо такі точки існують).

Правило дослідження функціїна найбільше (найменше) значення.

Якщо всі ці умови виконуються, то щоб знайти найбільше і найменше значення функції 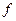, неперервної на відрізку, яка має на цьому відрізку скінченне число критичних точок, достатньо обчислити значення функції в усіх критичних точках і на кінцях відрізка та з одержаних чисел вибрати найбільше і найменше.

Під час дослідження функції на найменше (найбільше) значення корисними бувають такі твердження.

1. Точка, в якій функція набуває найменшого (найбільшого) значення, не змінюється при таких перетворення виразу, що задає функцію:

а) додаванні сталого доданка;

б) множенні на відмінне від нуля число (тільки при множенні на від’ємне число найменше значення переходить у найбільше і навпаки);

в) піднесенні до степеня з натуральним показником, якщо функція невід’ємна.

2. Якщо додатна функція 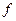набуває в деякій точці найменшого (найбільшого) значення, то функція і набувають у цій самій точці найбільшого (найменшого) значення.

Слід зазначити, що в окремих випадках, які визначаються властивостями цільової функції, досліджувати її на найбільше (найменше) значення можна не за вище сформульованим правилом, а на основі таких теорем.

Теорема 1.Якщо функція 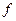, що визначена і неперервна на відрізку 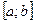, має тільки один мінімум (максимум), то він і є найменшим (найбільшим) значенням даної функції.

Теорема 2. Якщо функція 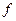, що визначена і неперервна на деякому проміжку 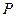, скінченному чи нескінченному, має тільки один мінімум (максимум), то він є найменшим (найбільшим) значенням даної функції.

Розглянуті теореми особливо зручні для користування у випадках, коли дослідження функції на мінімум (максимум) проводиться простіше, ніж обчислення і порівняння її значень в окремих точках (наприклад, якщо до виразу, що визначає цю функцію, входять буквені сталі).

Розглянемо окремі приклади таких задач.

Розпочнемо з задачі, яка розв’язується на основі правила дослідження функції на найбільше (найменше) значення.

Приклад 1.Покрівля повністю покритої спортивної зали має у поперечному перерізі арку параболи (рис. 1), вертикальна вісь якої проходить через центр зали. Точки кріплення на землі цієї арки знаходяться на відстані 40 м. Її вершина S розміщена на висоті 20 м від землі. Мають намір розділити залу на дві частини вертикальною завісою полотна MNPQ, яка дотикається землі і висить на горизонтальній балці MN. Виходячи з практичних міркувань, довжина балки може знаходитись тільки між двома екстремальними значеннями: 20 м і 30 м. Визначте, якої довжини повинна бути балка MN, щоб можна було розмістити найменш дорогу завісу.

	Після ознайомлення з умовою даної задачі доцільно обговорити алгоритм розв'язання, який складається з таких кроків:
Рис. 1

1) Складання рівняння параболи (Р), яка має вершину S(0;20) і проходить через точки А(–20;0), В(20;0). Побудова дуги (g) параболи (Р), яка відповідає невід'ємним у, в прямокутній системі координат.

2) Побудова цільової функції і складання рівняння залежності площі прямокутника MNPQ від довжини відрізка ОР=х, де xÎ[10;15].

3) Дослідження цільової функції з метою знаходження її найменшого значення.

4) Інтерпретація результату, одержаного при розв'язуванні практичної задачі всередині побудованої математичної моделі.

Вказівка. Цільовою функцією даної задачі буде функція 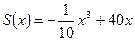, визначена на відрізку [10;15].

Відповідь. найменш дорогу завісу матимемо за умови, якщо довжина балки дорівнюватиме 30 .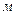

Особливістю цієї задачі є те, що під час її розв’язування в середині побудованої математичної моделі знаходять стаціонарну точку, яка виявляється точкою максимуму, а розв’язування задачі передбачає знаходження найменшого значення. Знайти це найменше значення цільової функції на вказаному відрізку, яким виявиться значення цільової функції у правому кінці відрізка, допоможе саме зазначене вище правило.

Зупинимось на прикладних задачах під час розв’язування яких використовуються згадані вище теореми.

Приклад 2.Для будівництва будинку прямокутної форми, зображеного на плані (рис.2) темним прямокутником, з площею 400 м² відведено ділянку у вигляді прямокутника, межі якої повинні знаходитись від будинку на відстані 36 і 16 м. Які розміри потрібно надати будинку, щоб площа ділянки ABCD була найменшою?

Рис. 2 Рис. 3

Розв’язання. В задачі необхідно визначити довжину і ширину прямокутника, що має площу 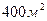, який розташований в середині площини прямокутника 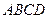, так що площа прямокутника 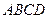буде найменшою. Сторони прямокутників взаємно паралельні і відстоять одна від іншої на і відповідно.

Позначимо довжину прямокутника 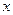, а ширину - 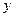. Його площа , звідки 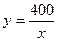. Площа прямокутника 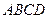дорівнює .

Отже, маємо цільову функцію , де 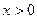. Дослідимо її на найменше значення. Знайшовши похідну функції і розв’язавши рівняння , з’ясуємо, що дана функція, яка визначена на множині додатних чисел, має єдину критичну точку . Оскільки при переході через цю точку знак похідної змінюється з ”-” на ”+”, то на основі достатньої умови існування екстремуму в точці, робимо висновок, що точка є точкою мінімуму функції .

Виходячи з єдності такої точки на інтервалі , можемо стверджувати, що в ній функція набуває найменшого значення: .

Отже, для того щоб площа ділянки була найменшою, будинок повинен мати розміри .

Відповідь. .

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ	\|	ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.