
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Лекція №7. УМОВИВІД ЯК СКЛАДНА ФОРМА МИСЛЕННЯ
ТАБЛИЦЯ №1. ОСНОВНІ ЗАКОНИ ЛОГІКИ І ЗАКОНИ ЛОГІКИ ВИСЛОВЛЮВАНЬ.
Кожна думка повинна бути достатньо обгрунтованою, але й достатнє обгрунтування повинне мати достатнє обгрунтування.
Четвертий закон логіки – закон достаточньої основи
Ним зумовлена ще одна корінна риса правильного мисления – його обгрунтованість, якісно визначені предмети так або інакше виникають з інших предметів і самі, у свою чергу, породжують треті. Це знаходить відображення й у нашому мисленні про предмети дійсности. Закон же формулюється так:
Межею обгрунтованості є закон, аксіома, очевидність, основані на фактах дійсності. Так, для людини, яка явилася свідком події, обгрунтуванням буде самий факт події, очевидцем якої вона була. Істинність законів, аксіом підтверджена практикою людства й не потребує тому нового підтвердження. Для підтвердження якого-небудь часткового випадку немає необхідності обгрунтовувавати його за допомогою особистого досвіду. Наприклад, якщо відомий закон Архімеда (усяке тіло, занурене у рідину, втрачає у своїй вазі рівно стільки, скільки важить витіснена ним рідина), то немає ніякого сенсу занурювати у рідину якийсь предмет, щоб з’ясувати, скільки він втрачає у вазі. Закон Архімеда буде достатньою основою для підтвердження будь-якого часткового випадку.
Таким чином, достатньою основою якоїсь думки може бути будь-яка інша вже перевірена та визнана думка, з якої з необхідністю випливає істинність даної думки.
Якщо з істинності судження А випливає істинність суджения В, то А є основою для В, а В – наслідком цієї основи. У свою чергу, В може бути основою для С. Так виникають логічні ланцюжки.
Найважливішою помилкою, пов’язаною з порушенням вимог закону достатньої основи, є помилка «удаваного слідування». Деякі удавані наслідки наведені у прикладах порушення закону суперечності: «Він і вона йшли разом по вулиці й сміялися – значить, у них роман» і т. д. Усе це приклади висновків з недостатніх основ.
Закон достатньої основи має важливе теоретичне й практичне значення. Фиксуючи увагу на судженнях, що обгрунтовують істинність висунутих положень, цей закон допомагає відокремити істинне від хибного та прийти до вірного висновку.
Приклад:Для того, щоб людина, яка скоїла злочин, могла бути притягнута до відповідальності, необхідно, щоб їй було більше, ніж 14 років.
Висновки. Закони логіки використовуються при умовиводах, аргументації думок, доведенні, розв’язанні теоретичних і практичних задач у кожній галузі знань. Вони мають загальнолюдський характер.
| № п/п | Назва закону | Його формулювання | Формула | Її прочитання | |||||
| Закон тотожності | Кожне висловлювання тотожне саме собі | А →А; А ↔А | «Якщо А, тоді А»; «А тоді і тільки тоді, коли А» | ||||||
| Закон несуперечності | Жодне висловлювання не може бути істинним одночасно із своїм запереченням | 
| «Неправильно, що А і не-А» | ||||||
| Закон виключеного третього | 3 двох суперечних суджень одне неодмінно є істинним, не дано. | 
| «А або не-А» | ||||||
| Закон достатньої підстави | Будь-яка істинна думка повинна бути достатньо обгрунтованою | Формального відображення не має | |||||||
| Закон подвійного речення: | |||||||||
| 5.1 | Закон зняття подвійного заперечення | Заперечення заперечення дає ствердження | 
| Якщо неправильно, що не-А, тоді А» | |||||
| 5.2 | Закон введення подвійного заперечення | Із ствердження випливає його подвійне заперечення | 
| «Якщо А, то хибно, ніби не-А» | |||||
| 5.3 | Поний закон подвійного заперечення | Подвійне заперечення тотожне ствердженню | 
| «Хибно, що не-А тоді і тільки тоді, коли А» | |||||
| Закони ідемпотентості: | |||||||||
| 6.1 | Закон ідемпотентості для кон'юнкції | Повтор висловлювання через сполучник кон'юнкції «і» є рівнозначним самому висловлюванню | (А ^ А) ↔ А | «А і А тоді і тільки тоді, коли А» | |||||
| 6.2 | Закон ідемпотентості для диз'юнкції | Повтор висловлювання через сполучник диз'юнкції «або» є рівнозначним самому висловлюванню | (А v А) ↔ А | А або А тоді і тільки тоді, коли А» | |||||
| Закони комутативності: | |||||||||
| 7.1 | Закон комутативності для кон'юнкції | Можна міняти місцями висловлювання, зв'язані сполучником кон'юнкції «і» | (АvВ)↔(ВvА) | «А і В тоді і тільки тоді, коли В і А» | |||||
| 7.2 | Закон комутативності для диз'юнкції | Можна міняти місцями висловлювання, зв'язані сполучником диз'юнкції «або» | (АvВ)↔(ВvА) | «А або В тоді і тільки тоді, коли В або А» | |||||
| Закони контрапозиції (простої і складної): | |||||||||
| 8.1 | Перший закон простої контрапозиції | Якщо з першого висловлювання випливає друге висловлювання, тоді із заперечення другого висловлювання випливає заперечення першого висловлювання | (А→В)→(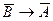 ) )
| «Коли відомо, що якщо А, то В, тоді якщо не-В. то не-А» | |||||
| 8.2 | Другий закон простої контрапозиції | Якщо із заперечення першого висловлювання випливає заперечення другого висловлювання, то з другого висловлювання випливає перше | ( )→(В→А) )→(В→А)
| «Коли відомо, що якщо не-А, то не-В, тоді якщо В, то А» | |||||
| 8.3 | Третій закон простої контрапозиції | Якщо із першого висловлювання випливає заперечення другого висловлювання, то з другого висловлювання випливає заперечення першого висловлювання | (А→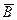 )→(В→ )→(В→ ) )
| «Коли відомо, що якщо А, то не-В, тоді якщо В, то не-А» | |||||
| 8.4 | Четвертий закон простої контрапозиції | Якщо із заперечення першого висловлювання випливає друге висловлювання, то із заперечення другого висловлювання випливає перше висловлювання | ( →В)→( →В)→(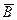 →А) →А)
| «Коли відомо, що якщо не-А, то В, тоді якщо не-В, то А» | |||||
| 8.5 | Перший закон складної контрапозиції | 3 першого і другого висловлювань випливає третє висловлювання тоді і тільки тоді, коли 3 першого висловлювання і заперечення третього висловлювання випливає заперечення другого висловлювання | 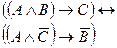
| «Коли відомо, що з А і В випливає С, то тоді і тільки тоді з А і не -С випливає не -В» | |||||
| 8.6 | Другий закон складної контрапозиції | 3 першого висловлювання випливає друге або третє висловлювання тоді і тільки тоді, коли із заперечення другого висловлювання випливає заперечення першого висловлювання або третє висловлювання | 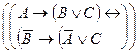
| «Коли відомо, що якщо А, то В або С, то тоді і тільки тоді з не-В випливає не-А або С» | |||||
| 9. | Закони асоціативності: | ||||||||
| 9.1 | Закон асоціативності для кон'юнкції | Висловлювання, з'єднані логічним сполучником кон'юнкції «і», можна по-різному поєднувати за допомогою дужок | ((А^В)^С)↔(А^(В^С)) | «(А і В) і С тоді і тільки тоді, коли А і (В і С)» | |||||
| 9.2 | Закон асоціативності для диз'юнкції | Висловлювання, з'єднані логічним сполучником диз'юнкції «або», можна по-різному поєднувати за допомогою дужок | ((А В) В) С)↔ (А С)↔ (А  (В (В С)) С))
| «(А або В) або С тоді і тільки тоді, коли А або (В або С)» | |||||
| Закони дистрибутивності: | |||||||||
| 10.1 | Закон дистрибутивності для кон'юнкції відносно диз'юнкції | Дозволяється у формулах розподіляти кон'юнкцію відносно диз'юнкції | ((А^(В^С)↔((А ^В)  (А^С)) (А^С))
| «А і (В або С), якщо і тільки якщо (А і В) або (А і С)» | |||||
| 10.2 | Закон дистрибутивності для диз'юнкції відносно кон'юнкції | Дозволяється у формулах розподіляти диз'юнкцію відносно кон'юнкції | ((А (В^С)↔ ((А (В^С)↔ ((А  В) ^ (А В) ^ (А  С)) С))
| «А або (В і С), якщо і тільки якщо (А або В) і (А або С)» | |||||
| Закони де Моргана: | |||||||||
| 11.1 | Перший закон де Моргана | Заперечення кон'юнкції висловлювань еквівалентне диз'юнкції заперечень цих висловлювань | 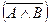 ↔( ↔(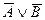 ) )
| «Хибно, що А і В тоді і тільки тоді, коли хибно, що А. або хибно, що В» | |||||
| 11.2 | Другий закон де Моргана | Заперечення диз'юнкції висловлювань еквівалентне кон'юнкції заперечень цих висловлювань | 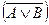 ↔( ↔( ) )
| «Хибно, що А або В тоді і тільки толі, коли хибно, що А і хибно і ні" | |||||
1. Загальна характеристика умовиводів.
2. Дедуктивний умовивід та його правила.
3. Категоричний силогізм.
4. Фігури і модуси категоричного силогізму.
5. Аналогія як умовивід.
Читайте також:
- II. Критерій найбільших лінійних деформацій
- III.4 Форматування тексту.
- IV. Виклад інформаційного матеріалу
- IV. Виклад інформаційного матеріалу
- IV. Критерій питомої потенціальної енергії деформації формозміни
- IV. Прийняття рішень у полі четвертої інформаційної ситуації
- R – розрахунковий опір грунту основи, це такий тиск, при якому глибина зон пластичних деформацій (t) рівна 1/4b.
- Tема 4. Фації та формації в історико-геологічному аналізі
- V. Прийняття рішень у полі п’ятої інформаційної ситуації
- VI. Прийняття рішень у полі шостої інформаційної ситуації
- Абсолютизація формально-технічних пошуків у мистецтві ХХ ст.
- Автоматизовані інформаційні системи для технічного аналізу товарних, фондових та валютних ринків.
| <== попередня сторінка | | | наступна сторінка ==> |
| З двох суджень, що взаємно виключають одне друге, одне істинне, друге хибне, а третього не дано. А є В або А не є В. | | | Загальна характеристика умовиводів |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |