• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розрахункові суми для оцінки ліній регресії.

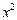
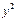
№ ознаки	х	у	xy			Y
. . .
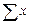
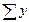
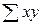
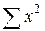
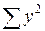
Разом						x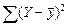

Із складеної нормальної системи рівнянь:

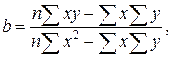
а = `y - b`x

Параметр 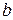– коефіцієнт регресії, який вказує, на скільки одиниць в середньому змінюється Y із зміною х на одиницю. У випадку прямого зв’язку 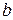– величина додатна, а при зворотному - від’ємна. Параметр а- вільний член рівняння регресії, це значення У при х=0.

Мірою тісноти зв’язку в кореляційно - регресійному аналізі виступає коефіцієнт детермінації 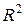, який відображає частку факторної дисперсії у загальній.

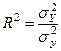
Дисперсію теоретичних значень (факторну) визначають за формулою:

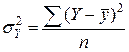
Загальна дисперсія ознаки 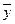дорівнює:

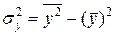
Коефіцієнт детермінації 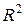характеризує ту частину варіації результативної ознаки у, яка відповідає лінійному рівнянню регресії і змінюється в межах 0£ R£1. Індекс кореляції 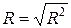характеризує тісноту зв’язку але економічної інтерпретації не має.

Лінійний коефіцієнт кореляції розраховується за формулою

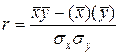
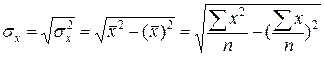
Перевірку істотності зв’язку в кореляційно - регресійному аналізі здійснюють за допомогою критичних значень 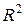та F-критерію. Фактичне значення F–критерію розраховують за формулою.

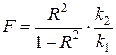
Ступені вільності залежать від параметрів рівняння (m): k₁=m-l, k₂=n-m.

Для лінійної моделі Y = a + bx, m=2.

У невеликих щодо обсягу сукупностях коефіцієнт регресії схильний до випадкових коливань. Тому необхідно визначати довірчі межі коефіцієнта регресії. Стандартна помилка коефіцієнта регресії обчислюється за формулою:

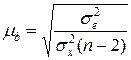
Величина граничної помилки

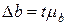
де t- коефіцієнт довіри, визначається для ймовірностей 0,95 , або 0.954 (1.96 і 2.00);

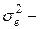залишкова дисперсія, яка визначається за формулою.

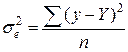або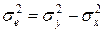

і характеризує варіацію результативної ознаки у, не пов’язану з варіацією факторної ознаки х. Довірчі межі коефіцієнта регресії складають:

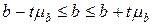
Якщо х збільшується на одиницю, рівень у лишається в наведених даних. В кінці рішення задачі прикладається графік кореляційного поля і лінії регресії Y = a + bx.

Читайте також:

1. DIMCLRE (РЗМЦВЛ) - колір виносних ліній (номер кольору). Може приймати значенняBYBLOCK (ПОБЛОКУ) і BYLAYER (ПОСЛОЮ).
2. II. Критерій найбільших лінійних деформацій
3. А) Мета і об'єкти грошової оцінки
4. А. Це наявність в однієї людини кількох ліній клітин з різним набором хромосом.
5. Адекватним фізичним критерієм оцінки її впливу на організм люди1
6. Активний опір ліній електропередачі
7. Аналіз відхилень – основний інструмент оцінки діяльності центрів відповідальності
8. Аналіз відхилень — основний інструмент оцінки діяльності центрів відповідальності
9. Аналіз загальної рівноваги розширює можливості оцінки ефективності функціонування ринкової економіки.
10. АНАЛІЗ ЛІНІЙНИХ МОДЕЛЕЙ ЕКОНОМІЧНИХ ЗАДАЧ
11. Аналіз методичних підходів до оцінки конкурентоспроможності фірми
12. Аналіз трифазного з’єднання з урахуванням опорів лінійних проводів

Переглядів: 484