• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розміщення з повтореннями та без повторень.

Малюнок № 1.21. Розв’язання задачі 2.

Отже, n(A)=n(B)+n(C)+n(K)-n(BÇC), 28=15+12+n(K)-7, n(K)=8 - кількість студентів, які займаються в інших секціях.

Інше правило комбінаторики відноситься до підрахунку числа кортежів, які можна утворити із елементів даних скінченних множин. Розглянемо дві скінченні множини А і В такі, що n(A)=m і n(B)=k. Утворимо множину А×В та знайдемо число її елементів, тобто n(А×В). Розглядаючи декартів добуток множин, ми з’ясували, що n(А×В)=n(А)•n(В)=m•k. Таким чином, можна сформулювати наступне правило.

Правило добутку: якщо елемент x із множини А можна вибрати m способами, а елемент y із множини B - k способами, то пару (x,y)єА×В можна вибрати m•k способами.

Символічно це правило можна записати так: n(А×В)=n(А)•n(В)=m•k. Його можна поширити на випадок будь-якої скінченної кількості множин. Покажемо застосування правила добутку на наступній задачі.

Задача: скільки трицифрових чисел можна записати, використовуючи цифри 1,2,3,4,5?

Розв’язання:

У цій задачі мова йде про п’ятиелементну множину А={1,2,3,4,5}, із елементів якої треба вибрати трьохелементні підмножини. Кожне трицифрове число являє собою впорядковану трійку цифр або впорядкований кортеж довжини три, наприклад: 111, 112, 121 тощо. Отже, для того, щоб скористатися правилом добутку, потрібно розглянути декартовий добуток трьох множин А×А×А. Оскільки, згідно з правилом добутку n(A×A×A)=n(A)×n(A)×n(A), то число трицифрових чисел, які можна скласти із цифр 1, 2, 3, 4, 5 дорівнює 125. Отже, із цифр 1, 2, 3, 4, 5 можна утворити 125 трицифрових чисел.

2.В останній задачі попереднього пункту ми утворювали впорядковані кортежі довжини три із елементів скінченної п’ятиелементної множини, причому деякі елементи повторювались 2 або 3 рази. Наприклад 112 i 111. В комбінаториці такі кортежі називають розміщеннями з повтореннями із заданих n елементів по k елементів. Число розміщень з повтореннями позначається так: Ã_n^k. Цей символічний запис читають: число розміщень з повтореннями із n елементів по k. Для визначення числа розміщень з повтореннями приймемо наступні означення та доведемо теорему.

Означення: розміщеннями з повтореннями із елементів n - елементної множини Х по k елементів називають кортежі довжини k, утворені із елементів цієї множини Х i компоненти яких повторюються.

Теорема 1: число розміщень з повтореннями із даних n елементів по k елементів обчислюється за формулою Ã_n^k=n^k.

Доведення:

Розглянемо скінченну множину Х таку, що n(Х)=n. Щоб утворити кортеж довжини k із елементів цієї множини Х, потрібно розглянути декартовий добуток множини Х саму на себе Х×Х×Х×...×Х, який містить k

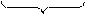
k

елементів, бо кожен кортеж довжини k є елементом декартового добутку. Згідно з правилом добутку число елементів цієї множини Х×Х×Х×...×Х

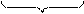
k

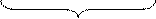дорівнює n(Х×Х×Х×...×Х)=n(Х)×n(Х)×n(Х)×...×n(Х)=n•n•n•...•n=nk. Теорему

k k k

доведено.

Застосування доведеної теореми проілюструємо на прикладі наступної задачі, подібну до якої ми раніше розв’язали, використовуючи правило добутку.

Задача: скільки п’ятицифрових чисел можна утворити із цифр 1, 2, 3, 4, 5?

Читайте також:

1. Вибір кількості та розміщення складської мережі
2. Вибір типу і місця розміщення водозабірних споруд
3. Вибір, розміщення, режими роботи компенсуючих пристроїв.
4. Вивіз капіталу та інвестиції в системі міжнародних економічних відносин. Напрямки та структура вивозу капі­талу. Форми вивозу та розміщення (інвестування) капіталу.
5. Вимоги до розвитку та розміщення об’єктів атомної енергетики
6. Вимоги до розміщення потенційно-небезпечних виробництв
7. Вплив науково-технічного прогресу на розміщення продуктивних сил
8. Вплив розміщення оборотних коштів підприємства на його фінансовий стан.
9. Грошовий потік від розміщення 3-літньої облігаційної позики, тис. грн.
10. Грошовий потік від розміщення 5-літньої облігаційної позики, тис. грн.
11. Демографічні передумови розміщення продуктивних сил.
12. Економічні закони і закономірності розміщення продуктивних сил.

Переглядів: 2761