
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Необхідність розширення множини цілих чисел.
ПЛАН.
Змістовний модуль 5.2. «Раціональні числа.».
МОДУЛЬ У. «РОЗШИРЕННЯ ПОНЯТТЯ ПРО ЧИСЛО».
1. Необхідність розширення множини цілих чисел.
2. Поняття дробу. Рівність дробів. Основна властивість дробів. Скорочення дробів та їх зведення до спільного знаменника. Нескоротні дроби.
3. Невід’ємні раціональні числа та їх властивості.
4. Відношення порядку на множині невід’ємних раціональних чисел.
5. Додавання і віднімання невід’ємних раціональних чисел. Теореми про існування та єдиність суми і різниці. Властивості (закони) додавання.
6. Множення і ділення невід’ємних раціональних чисел. Теореми про існування та єдиність добутку та частки. Властивості (закони) множення.
7. Властивості множини невід’ємних раціональних чисел.
8. Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.
9. Додатні раціональні числа як нескінченні періодичні десяткові дроби. Чисті та мішані періодичні дроби та їх перетворення у звичайні.
10. Множина раціональних чисел, модуль раціонального числа, операції над раціональними числами. Властивості множини раціональних чисел.
ЛІТЕРАТУРА:[1] – с. 172-238; [2] – с. 193-246, 325-340; [3] – с. 181-196.
1. Подальший розвиток людського суспільства довів необхідність розширення множини цілих чисел, бо їх не вистачало як для потреб практики, так і для математики. На практиці зустрічалися випадки, коли неможливо було визначити результат вимірювання чи виконати операцію ділення у випадках виду 20:3. З точки зору математики це означало, що, по-перше, існують несумірні відрізки, по-друге, рівняння виду 7х=48 не має цілих коренів. Все це призвело до виникнення поняття дробу, які виникли із необхідності вимірювання величин та розв’язування рівнянь виду ах=b. Спочатку виникли конкретні дроби, кожен з яких мав свою назву та позначення. Пізніше з’являються основні одиничні дроби виду  (Єгипет). У стародавній Греції з’являються і звичайні дроби.
(Єгипет). У стародавній Греції з’являються і звичайні дроби.
Історія розвитку людства та математики свідчать, що дроби позначали по-різному, але вже у І ст. до н. е. Герон і Діофант застосовували риску дробу, але знаменник писали над рискою дробу, а чисельник – під нею. В У столітті до н.е. греки вміли виконувати всі дії над звичайними дробами. Першим вченим Європи, який застосував риску дробу та сучасний запис дробів, був італійський математики Леонардо Пізанський (або Леонардо Фібоначчи – син Боначчи).
Дроби у стародавній Русі називали долями або ламаними числами, а деякі з них позначали і називали так: 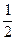 - половина, полтина;
- половина, полтина;  - четь;
- четь;  - полчеть;
- полчеть; 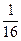 – полполчеть;
– полполчеть;  – полполполчеть (мала четь);
– полполполчеть (мала четь);  - седьмина;
- седьмина;  - треть;
- треть; 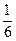 – полтреть;
– полтреть; 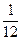 – полполтреть;
– полполтреть; 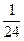 – полполполтреть (мала треть);
– полполполтреть (мала треть);  – п’ятина;
– п’ятина;  – десятина тощо. Такий запис та назви існували до ХУІ століття та були витіснені за Петра І.
– десятина тощо. Такий запис та назви існували до ХУІ століття та були витіснені за Петра І.
Десяткові дроби незалежно були винайдені із потреб практики в різні часи в Азії та Європі. Досить повне й систематичне трактування одержують десяткові дроби у працях середньоазіатського вченого аль-Коші в 20-х роках ХУ ст. Незалежно від нього в 80-х роках ХУІ ст. десяткові дроби були «відкриті» заново в Європі нідерландським математиком С.Стевіном. Кома, як знак, що відділяє цілу частину від дробової, вперше була застосована італійським астрономом Дж.Маджині (1555-1617 рр.). Окрім того, німецький математик Хр.Клавіус у 1593 році застосовував для цієї мети крапку.
Розглядаючи цілі числа, ми ввели поняття від’ємних чисел, але поява від’ємних чисел і дробових чисел в практиці повсякденної діяльності та в математиці не співпадають. Історія людства свідчить, що раніше виникли дробові числа, які більше застосовувалися у практичній діяльності людини, ніж від’ємні. Так, від’ємні числа почали застосовуватися лише у І ст. до н. е. у Китаї у зв’язку з розв’язуванням рівнянь. На письмі їх писали чорнилами різних кольорів: додатні числа писали червоним кольором (китайською «чен»), а від’ємні – чорним кольором (китайською «фу»). Індійські математики Брахмагупта (УІІ ст.) та Бхаскара (ХІІ ст.) дали правила дій над від’ємними числами. У Європі від’ємні числа вперше почав використовувати Л.Фібоначчи (ХІІ-ХІІІ ст.). Німецький математик М.Штіфель (ХУІ ст.) називав їх числами меншими, ніж ніщо. Протягом всього цього періоду від’ємні числа називали абсурдними, недійсними тощо. Тільки після того, як у ХУІІ ст. видатний французький вчений Р.Декарт зобразив на числовій прямій додатні числа праворуч, а від’ємні – ліворуч від початку відліку, їх почали визнавати. Отже, розвиток практики та потреби математики з необхідністю вимагають розширення множини цілих чисел.
Таким чином, розширювати множину цілих чисел будемо так, щоб виконувалися наступні вимоги: 1) до нової множини приєднаємо числа нової природи - дробові числа; 2) визначимо арифметичні операції додавання, віднімання, множення і ділення над дробовими числами так, щоб вони не суперечили правилам виконання дій над цілими числами; 3) поширимо основні закони (властивості) дій над цілими числами на числа нової природи; 4) поставимо завдання про необхідність виконання дії ділення (крім ділення на нуль!) для будь-яких чисел нової природи, тобто буде можливість розв’язати рівняння виду ах=b для будь-яких чисел нової множини.
Читайте також:
- Бюджетні запити: їх суть, необхідність складання та аналіз
- Бюджетні множини й лінії бюджетного обмеження
- Введення чисел.
- Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
- Визначення множини допустимих планів задачі ЛП
- Визначення суми на множині цілих невід’ємних чисел, її існування та єдиність. Операція додавання та її основні властивості (закони).
- Визначення та необхідність контролю.
- Виникнення внутрішнього аудиту та його необхідність
- Відносини власності в Україні. Необхідність різноманітних форм власності.
- Відношення еквівалентності та порядку, їх властивості. Впорядковані множини. Зв'язок відношення еквівалентності з розбиттям множини на класи, що попарно не перетинаються.
- Відношення порядку на множині дійсних чисел.
- Відношення порядку на множині невід’ємних раціональних чисел.
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |