
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Теоретичні відомості
Для представлення інформації в пам'яті ЕОМ використовується двійковий спосіб кодування.
Елементарна комірка пам'яті ЕОМ має довжину 8 біт (байт). Кожен байт має свій номер (його називають адресою). Найбільшу послідовність біт, що ЕОМ може обробляти як єдине ціле, називають машинним словом. Довжина машинного слова залежить від розрядності процесора і може бути рівною 16, 32 бітам і т.д.
Для кодування символів досить одного байта. При цьому можна представити 256 символів (з десятковими кодами від 0 до 255). Набір символів персональних ЕОМ IBM PC найчастіше є розширенням коду ASCII (American Standard Code for Information Interchange — стандартний американський код для обміну інформацією).
У деяких випадках при представленні в пам'яті ЕОМ чисел використовується змішана двоїчно-десяткова система числення, де для збереження кожного десяткового знака потрібний напівбайт (4 біти) і десяткові цифри від 0 до 9 представляються відповідними двійковими числами від 0000 до 1001. Наприклад, упакований десятковий формат, призначений для збереження цілих чисел з 18-ю значущими цифрами і займає в пам'яті 10 байт (старший з яких знаковий), використовує саме цей варіант.
Інший спосіб представлення цілих чисел — додатковий код. Діапазон значень величин залежить від кількості біт пам'яті, відведених для їхнього збереження. Наприклад, величини типу Integer (усі назви типів даних тут і нижче представлені в тому вигляді, у якому вони прийняті в мові програмування Turbo Pascal). В інших мовах такі типи даних теж є, але можуть мати інші назви лежать у діапазоні від –32768 (–215) до 32767 (215–1) і для їхнього збереження вигляділяється 2 байти; типу LongInt — у діапазоні від –231 до 231–1 і розміщуються в 4 байтах; типу Word — у діапазоні від 0 до 65535 (216–1) (використовується 2 байти) і т.д.
Як видно з прикладів, дані можуть бути інтерпретовані як числа зі знаками, так і без знаків. У випадку представлення величини зі знаком лівий (старший) розряд указує на позитивне число, якщо містить нуль, і на негативне, якщо — одиницю.
Узагалі, розряди нумеруються з права наліво, починаючи з 0. Нижче показана нумерація біт у двійковому машинному слові.
Додатковий код позитивного числа збігається з його прямим кодом. Прямий код цілого числа може бути отриманий у такий спосіб: число переводиться в двійкову систему числення, а потім його двійковий запис ліворуч доповнюють такою кількістю незначних нулів, скільки вимагає тип даних, до якого належить число. Наприклад, якщо число 37(10) = 100101(2) оголошено величиною типу Integer, то його прямим кодом буде 0000000000100101, а якщо величиною типу LongInt, те його прямий код буде 00000000000000000000000000100101. Для більш компактного запису частіше використовують шістнадцятирічний код. Отримані коди можна переписати відповідно як 0025(16) і 00000025(16).
Додатковий код цілого негативного числа може бути отриманий за наступним алгоритмом:
1) записати прямий код модуля числа;
2) інвертувати його (замінити одиниці нулями, нулі — одиницями);
3) додати до інверсного коду одиницю.
Наприклад, запишемо додатковий код числа (–37), інтерпретуючи його як величину типу LongInt:
1) прямий код числа 37 є 00000000000000000000000000100101;
2) інверсний код 11111111111111111111111111011010;
3) додатковий код 11111111111111111111111111011011 або FFFFFFDB(16).
При одержанні числа за його додатковим кодом насамперед необхідно визначити його знак. Якщо число виявиться позитивним, то просто перевести його код у десяткову систему числення. У випадку негативного числа необхідно виконати наступний алгоритм:
1) відняти з коду числа 1;
2) інвертувати код;
3) перевести в десяткову систему числення. Отримане число записати зі знаком мінус.
Приклади. Запишемо числа, що відповідають додатковим кодам:
а) 0000000000010111. Оскільки в старшому розряді записаний нуль, то результат буде позитивним. Це код числа 23.
б) 1111111111000000. Тут записаний код негативного числа. Виконуємо алгоритм:
1) 1111111111000000(2) – 1(2) = 1111111110111111(2); 2) 0000000001000000; 3) 1000000(2) = 64(10).
Відповідь: –64.
У табл. 1 наведено перші 16 натуральних чисел, записаних в десятковій, двійковій, вісімковій та шістнадцятковій системах числення.
1. Системи числення
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
2. Кодіровка ASCII
| Шістнадцятковий код | |||||||||||||||
| nul | soh | stx | etx | eot | enq | ask | bel | ||||||||
| bs | ht | 0a | nl | 0b | vt | 0c | np | 0d | cr | 0e | so | 0f | si | ||
| dle | dc1 | dc2 | dc3 | dc4 | nak | syn | etb | ||||||||
| can | em | 1a | sub | 1b | esc | 1c | fs | 1b | gs | 1e | rs | 1f | us | ||
| sp | ! | " | # | $ | % | & | ' | ||||||||
| ( | ) | 2a | * | 2b | + | 2c | , | 2d | - | 2e | . | 2f | / | ||
| 3a | : | 3b | ; | 3c | < | 3d | = | 3e | > | 3f | ? | ||||
| @ | A | B | C | D | E | F | G | ||||||||
| H | I | 4a | J | 4b | K | 4c | L | 4d | M | 4e | N | 4f | O | ||
| P | Q | R | S | T | U | V | W | ||||||||
| X | Y | 5a | Z | 5b | [ | 5c | \ | 5d | ] | 5e | ^ | 5f | _ | ||
| ` | a | b | c | d | e | f | g | ||||||||
| h | i | 6a | j | 6b | k | 6c | l | 6d | m | 6e | n | 6f | o | ||
| p | q | r | s | t | u | v | w | ||||||||
| x | y | 7a | z | 7b | { | 7c | | | 7d | } | 7e | ~ | 7f | del |
Пояснення. У таблиці символи представлені у вигляді сітки, наприклад, код букви A є 41, оскільки ця буква перебуває на перетині рядка 40 і стовпця 1 (40 + 1 = 41). У таблицях для подання кодів використовуються числа в 16-ому поданні, тобто кожен розряд числа може набувати значень 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Щоб відрізняти шістнадцяткові числа від звичних десяткових, їх пишуть із префіксом 0x, наприклад, код вищезгаданої букви A є 0x41. Зручність 16-го подання числа полягає в тому, що кожен розряд при поданні відповідає чотирьом бітам, тобто двозначне 16-е число — це вісім біт, що дорівнює одному байту, отже восьмибітовий код виражається числами від 0x00 до 0xFF. Відповідно, двохбайтовий (шістнадцятибітовий) код виражається числами від 0x0000 до 0xFFFF. Останнє число в десятковому вигляді дорівнює 65535. Коли очевидно, що використовується 16-е подання числа, як у таблицях, префікс 0x можна опускати.
Коди перших двох рядків таблиці ASCII являють собою деякі команди (не символи), тому відсутні. Відповідно до сформованих правил, таблиця ASCII займає першу половину (0x00-0x7F) будь-якої восьмибітової таблиці: можуть розрізнятися лише останніми 128 символами (0x80-0xFF). Над кожним символом у таблицях, приводиться його шістнадцятибітовий Unicode цього знака. Оскільки й таблиця Unicode починається з ASCII, то в даній таблиці "юнікоди" і восьмибітові коди збігаються.
3. Кодіровка ASCII
| Вісімковий код | |||||||||||||||
| nul | soh | stx | etx | eot | enq | ack | bel | ||||||||
| bs | ht | nl | vt | np | cr | so | si | ||||||||
| dle | dc1 | dc2 | dc3 | dc4 | nak | syn | etb | ||||||||
| can | em | sub | esc | fs | gs | rs | us | ||||||||
| sp | ! | " | # | $ | % | & | ' | ||||||||
| ( | ) | * | + | , | - | . | / | ||||||||
| : | ; | < | = | > | ? | ||||||||||
| @ | A | B | C | D | E | F | G | ||||||||
| H | I | J | K | L | M | N | O | ||||||||
| P | Q | R | S | T | U | V | W | ||||||||
| X | Y | Z | [ | \ | ] | ^ | _ | ||||||||
| ` | a | b | c | d | e | f | g | ||||||||
| h | i | j | k | l | m | n | o | ||||||||
| p | q | r | s | t | u | v | w | ||||||||
| x | y | z | { | | | } | ~ | del |
4. Альтернативна кодова таблиця
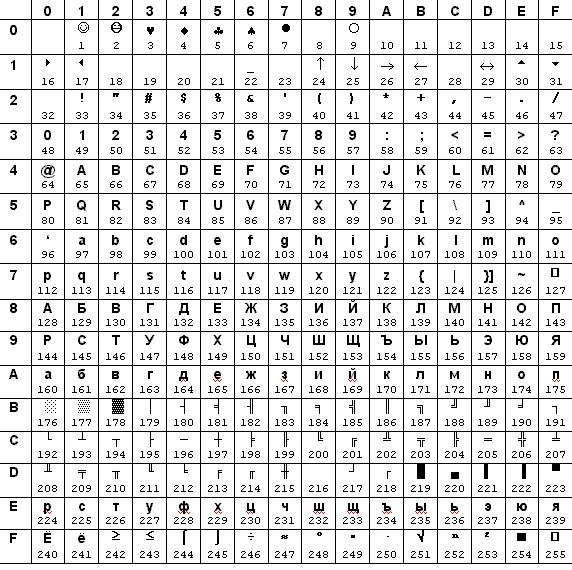
Завдання на лабораторну роботу
1. Переведіть задане число з десяткової системи числення в двійкову.
2. Перевести число з двійкової системи числення в десяткову.
3. Зашифруйте наведений текст, використовуючи таблицю ASCII-кодів (Табл. 2, 3).
4. Дешифруйте цей текст, використовуючи таблицю ASCII-кодів (Табл. 4).
5. Запишіть прямий код числа, інтерпретуючи його як восьмибітове ціле без знака.
6. Запишіть додатковий код числа, інтерпретуючи його як восьмибітове ціле зі знаком.
7. Запишіть прямий код числа, інтерпретуючи його як шістнадцятибітове ціле без знака.
8. Запишіть додатковий код числа, інтерпретуючи його як шістнадцятибітове ціле зі знаком.
9. Запишіть у десятковій системі числення ціле число, якщо дано його додатковий код.
10. Створіть рекурсивну функцію (програму) переводу арабських чисел в римські, використовуючи програму MatLab.
Читайте також:
- II.ТЕОРЕТИЧНІ ПИТАННЯ КУРСОВОЇ РОБОТИ
- IX. Відомості про військовий облік
- IX. Відомості про військовий облік
- Q Конституція України від 28 червня 1996 р. // Відомості Верховної Ради України – 1996 - № 30 – Ст. 141
- V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
- Активне управління інвестиційним портфелем - теоретичні основи.
- Білковий обмін: загальні відомості
- Біографічні відомості
- Боротьба з проявами національної самосвідомості
- Вальниці ковзання. Загальні відомості
- Види правосвідомості
- Виникнення і розвиток свідомості у людини.
| <== попередня сторінка | | | наступна сторінка ==> |
| Лабораторна робота № 2 | | | Варіант 1 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |