• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Трикутник Паскаля

Французький математик Блез Паскаль (1623-1662) склав таблицю з|із| біноміальних коефіцієнтів. Вона вийшла трикутною, оскільки із|із| збільшенням ступеня|міри| бінома кількість коефіцієнтів також збільшується. Тому цю таблицю називають трикутником Паскаля. На мал. 4.1 показаний трикутник Паскаля, в якому використані формальні позначення біноміальних коефіцієнтів. На мал. 4.2 приведений трикутник Паскаля з|із| числовими значеннями біноміальних коефіцієнтів.

Цього значення може бути набуте за допомогою формули (4.2). Проте|однак| трикутник Паскаля дає можливість|спроможність| розраховувати біноміальні коефіцієнти без застосування|вживання| даної формули. Якщо відомі коефіцієнти в якому-небудь рядку таблиці, то можна легко обчислити|обчисляти,вичислити| коефіцієнти в сусідньому рядку, який знаходиться|перебуває| нижче першого. Для визначення кожного коефіцієнта нижнього рядку потрібно скласти два коефіцієнти верхнього рядка, які знаходяться|перебувають| зліва|ліворуч| і справа безпосередньо над коефіцієнтом, що розраховується. Таким чином, рухаючись|сунучись| від вершини трикутника вниз, можна послідовно розрахувати біноміальні коефіцієнти для будь-якого кінцевого|скінченного| ступеня|міри| бінома Ньютона.

Мал. 4.1. Трикутник Паскаля

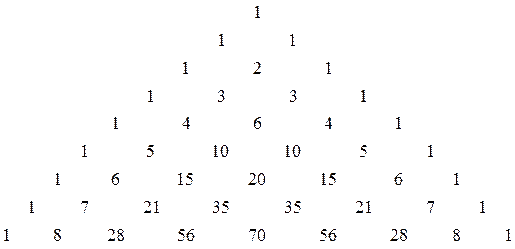
Мал. 4.2. Трикутник Паскаля з|із| числовими значеннями коефіцієнтів

Читайте також:

1. Виведення формул для знаходження площі паралелограма, трикутника, трапеції. Формули для знаходження площ поверхонь просторових геометричних фігур.
2. Гідростатика нестисливої рідини. Закон Паскаля. Гідростатичний тиск. Закон Архімеда
3. З'єднання споживачів трикутником. У загальному випадку несиметричного навантаження активна потужність трифазного приймача дорівнює сумі активних потужностей окремих фаз
4. Загальна ознака подільності Б.Паскаля. Ознаки подільності цілих невід’ємних чисел на 2, 3, 4, 5, 9, 25.
5. Закон Паскаля
6. Закон Паскаля. Гідравлічний прес.
7. З’єднання у трикутник
8. З’єднання фаз генератора та споживача трикутником
9. Паралактичний трикутник
10. Перетворення трикутників опорів в еквівалентну зірку та навпаки
11. Побудова трикутника за трьома сторонами.
12. Розрахунок ланцюгів оснований на перетворені трикутника опорів в еквівалентну зірку та навпаки

Переглядів: 4060