• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розфарбовування графа, хроматичний поліном

Припустимо|передбачимо|, що перед нами стоїть завдання|задача|: розфарбувати карту світу так, щоб кожна країна мала свій власний колір|цвіт|. Оскільки на світі існує декілька сотень держав, то, природно, буде потрібно достатньо|досить| багато різних фарб|барв|.

Спростимо завдання|задачу|. Використовуватимемо меншу кількість фарб|барв|, але|та| при цьому не допускатимемо, щоб сусідні країни, що мають загальні|спільні| межі|кордони|, були забарвлені|пофарбовані| в один колір|цвіт|. Виникає питання: яка мінімальна кількість фарб|барв| потрібна, щоб задовольнити цій умові?

Відповісти на це питання можна за допомогою теорії графів. Для цього потрібно представити|уявити| карту світу у вигляді графа, кожна вершина якого відповідає окремій країні, а ребро між суміжними вершинами відповідає наявності між країнами загальної|спільної| межі|кордону|.

Довільна функція 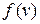на безлічі вершин графа називається розфарбовуваннямграфа. Розфарбовування називається правильним, якщо 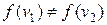для будь-яких суміжних вершин 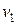і 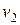. Мінімальне число k, при якому граф G є|з'являється,являється| k- розфарбовуваємим,| називається хроматичним числом графа .

Граф називається порожнім|пустим|, якщо в ньому видалені|віддалені| всі ребра і вершини ізольовані одна від одної. Граф називається повним|цілковитим|, якщо в ньому не можна додати|добавити| нове ребро, не додавши|добавивши| при цьому одночасно нову вершину.

Теорема 12.7 (Брукса). Для будь-якого графа G, що не є|з'являється,являється| повним|цілковитим|, , якщо 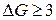– максимальна із|із| ступенів|мір| вершин графа.

Для визначення кількості способів розфарбовування графа в x кольорів|цвіту|, необхідно скласти хроматичний поліном P(G, x). Значення полінома при деякому конкретному 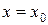рівне числу правильних розфарбовувань графа в кольорів|цвіту|.

Існує лема, що затверджує|стверджує,ухвалює|, що хроматичний поліном графа має вигляд|вид|

, (12.4)

де – граф, одержаний|отриманий| з|із| G додаванням|добавкою| ребра (u, v), а граф виходить з|із| G ототожненням вершин u і v.

Інший варіант леми:

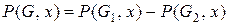, (12.5)

де – граф, одержаний|отриманий| з|із| G видаленням|віддаленням| ребра (u, v), а граф виходить з|із| G ототожненням вершин u і v.

Операцію ототожнення вершин u і v називають також стяганням ребра (u, v).

Обидва варіанти леми складають основу для хроматичної редукції графа (reduction – «скорочення» на англійському). Хроматична редукція графа – представлення графа у вигляді декількох порожніх|пустих| або повних|цілковитих| графів, сума хроматичних поліномів яких рівна хроматичному поліному графа. Очевидно, що хроматичний поліном порожнього|пустого| графа 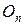рівний (кожна вершина може бути розфарбована незалежно від інших), а для повного|цілковитого| графа 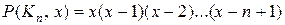. Останній вираз|вираження| називають факторіальним ступенем|мірою| змінної x: .

Розкладання по порожніх|пустих| і повних|цілковитих| графах зв'язані. Факторіальний ступінь|міру| можна представити|уявити| у вигляді полінома:

, (12.6)

де – числа Стірлінга першого роду. І навпаки, ступінь|міру| можна виразити|виказати,висловити| через факторіальні ступені|міри|:

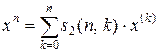, (12.7)

де – числа Стірлінга другого роду, що володіють наступними|слідуючими| властивостями:

при 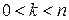, (12.8)

при , при .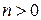

При отриманні|здобутті| хроматичного полінома можуть бути корисні наступні|такі| теореми.

Теорема 12.8. Коефіцієнти хроматичного полінома складають знакозмінну послідовність.

Теорема 12.9. Абсолютна величина другого коефіцієнта хроматичного полінома рівна числу ребер графа.

Теорема 12.10. Найменше число i, для якого відмінний|інший| від нуля коефіцієнт при в хроматичному поліномі графа G, рівне числу компонент зв'язності графа G.

Окрім|крім| вершинного розфарбовування, існує ще реброве розфарбовування і розфарбовування граней.

Приклад|зразок| 12.7. Знайти хроматичний поліном графа, показаного на мал. 12.8.

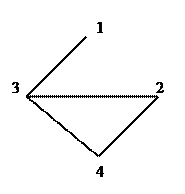
Мал. 12.8

Рішення|розв'язання,вирішення,розв'язування|. Залежно від числа ребер графа можна використовувати розкладання (12.4) або (12.5). Якщо граф майже повний|цілковитий|, то, додавши|добавивши| декілька ребер по розкладанню (12.4), одержимо|отримаємо| хроматичний поліном у вигляді суми факторіальних ступенів|мір|. Якщо ж ребер мало і для отримання|здобуття| порожнього|пустого| графа потрібно видалити|знищити,віддалити| тільки|лише| декілька ребер, то слід використовувати розкладання (12.5) з|із| видаленням|віддаленням| ребер. Такі дії називаються хроматичною редукцією.

1. Хроматична редукція по порожніх|пустих| графах. Скористаємося спочатку лемою (12.5). Видаляючи|знищуючи,віддаляючи| ребра і ототожнюючи відповідні вершини (стягуючи ребра), зведемо початковий|вихідний| граф до порожніх|пустих| граф. Спочатку розкладемо граф на два, прибравши, а потім стягнув| ребро 1-3. Виконану дію запишемо у вигляді умовної рівності:

Тут операція віднімання відноситься не до самого графа, а до його хроматичного полінома. Таким чином, остання рівність означає, що 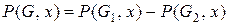. Для скорочення запису позначення P(...) опускатимемо. Далі розкладемо кожного з графів і ,користуючись тією ж лемою.

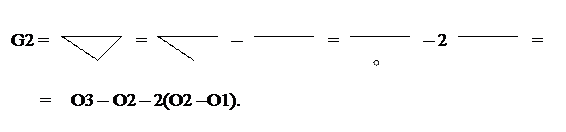
Приведемо подібні члени:

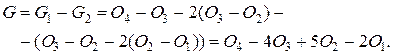(12.9)

У результаті одержимо|отримаємо| шуканий хроматичний поліном:

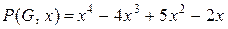. (12.10)

Розкладання (12.9) називається хроматичною редукцією графа по порожніх|пустих| графах.

Очевидно, що результат відповідає затвердженням теорем 12.8-12.10. Коефіцієнти в (12.10) утворюють знакозмінну послідовність, а коефіцієнт при 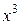рівний чотирьом – числу ребер. Найменший ступінь|міра| x в поліномі рівний 1, тобто числу компонент зв'язності графа.

2. Хроматична редукція по повних|цілковитих| графах. Додавши|добавивши| до зображеного|змальованого| на мал. 12.8 графа ребро 1–4, одержимо|отримаємо| граф з|із| великим числом ребер. Потім в початковому|вихідному| графі ототожнимо вершини 1 і 4. В результаті одержимо|отримаємо| двох графів.

Ототожнення вершин приводить|призводить,наводить| до зменшення порядку|ладу| і іноді|інколи| розміру графа. Другий граф – це повний|цілковитий| граф, його перетворювати більше не потрібно. До першого графа додамо|добавимо| ребро 1–2 і ототожнимо вершини 1 і 2:

У результаті одержимо|отримаємо|

(12.11)

Хроматичний поліном прийме вигляд|вид|

(12.12)

Розкладання (12.11) називається хроматичною редукцією графа по повних|цілковитих| графах.

Обидва способи дали один результат, і з|із| редукції по повних|цілковитих| графах легко одержати|отримати| редукцію по порожніх|пустих|. Для цього досить розкрити дужки і привести подібні члени, як в (12.12). Проте|однак| зворотна дія не очевидна. Для того, щоб поліном, одержаний|отриманий| з|із| порожніх|пустих| графів, виразити|виказати,висловити| у вигляді суми факторіальних ступенів|мір|, необхідні числа Стірлінга 2-го роду. Згідно рекурентним формулам (12.8) маємо наступні|слідуючі| числа:

,

,

,

.

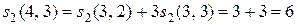Користуючись (12.7) і знайденими числами Стірлінга 2-го роду, одержимо|отримаємо|

,

,

.

Проведемо|виробимо,справимо| перетворення хроматичного полінома:

Хроматичне число графа краще всього одержати|отримати|, розклавши хроматичний поліном на множники:

.

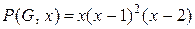Мінімальне натуральне число x, при якому не звертається|обертається| в нуль, рівне 3. Звідси слідує|прямує| 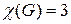. Оскільки|тому що| максимальний ступінь|міра| вершин графа, виконується оцінка .

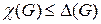Читайте також:

1. Кільце поліномів та його властивості.
2. Корені поліномів та їх властивості.
3. Означення поліному. Дії над поліномами.
4. Поліноміальний метод факторизації Чалмерса
5. Розв’язок плоскої задачі теорії пружності в поліномах (цілих функціях).

Переглядів: 1483