• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розв’язок плоскої задачі теорії пружності в поліномах (цілих функціях).

Розв’язок плоскої задачі може бути здійснено напівоберненим методом. Для цього спочатку задаються аналітичною формою функції напружень, яка б задовольняла бігармонічному рівнянню (5.5), а потім визначають, яким навантаженням на контурі вона відповідає. В якості бігармонічної функції можна приймати алгебраїчні поліноми різних ступенів.

Поліном першого ступеня 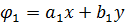, зазвичай, не використовують як функцію напружень, оскільки напруження, обчислені за формулами (5.3) будуть дорівнювати нулеві.

Розглянемо функцію напружень задану за допомогою поліному другого ступеня:

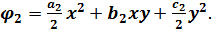(5.7)

Четверті похідні цієї функції дорівнюють:

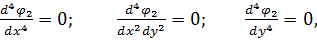
при цьому бігармонічне рівняння (5.5) перетворюється на тотожність при будь-яких значеннях коефіцієнтів a₂, b₂, c₂. Таким чином поліном другого ступеня є бігармонічною функцією та може бути використаний для вирішення плоскої задачі.

Якщо функцію полінома прийняти у вигляді поліному третього ступеню:

(5.8)

то бігармонічне рівняння (5.5) знову буде обертатися на тотожність при довільних величинах коефіцієнтів a₃, b₃, c₃, d₃, тобто поліном третього ступеня є бігармонічною функцією і також може бути використаний для вирішення плоскої задачі.

Задамо функцію φ (x, y) у вигляді поліному четвертого ступеню:

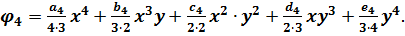(5.9)

Четверті похідні цієї функції:

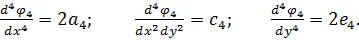
Підставивши їх в бігармонічне рівняння (5.5), отримаємо:

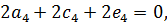
звідки

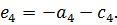
Таким чином, не всі коефіцієнти поліному четвертого ступеню довільні. Незалежними можуть бути тільки чотири коефіцієнта, а п’ятий визначають користуючись останнім співвідношенням. Відповідно для того щоб поліном четвертого ступеню був бігармонічною функцією, він повинен мати наступний вигляд:

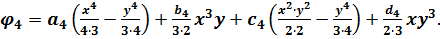(5.10)

Розглянемо поліном п’ятого ступеню:

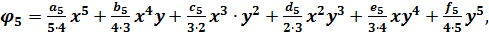(5.11)

За аналогією з поліномом четвертого ступеню, виконаємо відповідні перетворення над поліномом п’ятого ступеню (5.11) після чого він стає бігармонічним рівнянням та набуває вигляду:

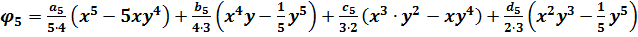(5.12)

В такому вигляді поліном п’ятого ступеню може бути застосований для розв’язку плоскої задачі.

За допомогою алгебраїчних поліномів можна розв’язати декілька простих задач:

Задачу про чистий згин балки, згин балки на двох опорах під дією рівномірно розподіленого навантаження, задачу про трикутну підпірну стінку.

Читайте також:

1. А .Маршалл - основоположник неокласичної теорії.
2. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
3. Алгоритм розв’язання задачі
4. Алгоритм розв’язання розподільної задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі
10. Алгоритм розв’язування задачі
11. Алгоритм розв’язування задачі оптимізації в Excel
12. Альтернативні теорії вартості

Переглядів: 960