• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розв’язок плоскої задачі теорії пружності методом тригонометричних рядів Рибьєра-Фурьє.

В якості функції напружень φ (x, y) можна прийняти тригонометричні ряди. Дослідимо тригонометричну функцію:

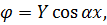(5.13)

де Y – функція, яка залежить тільки від координати y;

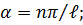(5.14)

n – будь-яке ціле число; ℓ - довжина пластинки в напрямку осі х.

З’ясуємо, при яких умовах функція φ буде бігармонічною, тобто задовольнятиме умову (5.5). Підрахуємо четверті похідні функції φ:

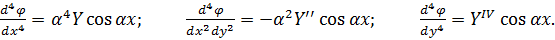
Підставивши їх в рівняння (5.5), отримаємо:

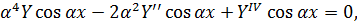
або

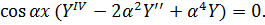
Це рівняння обертається на тотожність при будь-якому значенні аргументу х, якщо Y(y) задовольняє диференціальному рівнянню

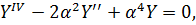
розв’язок якого можна представити за допомогою гіперболічних функцій:

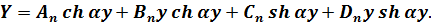(5.15)

Підставивши цей розв’язок в вираз (5.13), отримаємо бігармонічну функцію у вигляді:

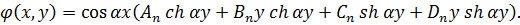
Аналогічно можна довести, що функція

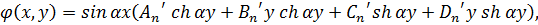
також є бігармонічною і може бути застосована для розв’язку плоскої задачі.

Якщо числу n в співвідношенні (5.14) надавати різні значення, то кожен раз будуть отримані нові функції, які будуть відрізняються значеннями параметра α та сталими A_n, B_n, C_n, D_n. Тому загальний розв’язок бігармонічного рівняння (5.5) може бути представлений, як сума всіх його можливих особистих розв’язків, тобто у вигляді нескінченного ряду:

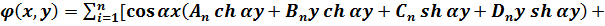
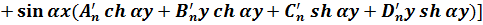(5.16)

Сталі A_n, B_n,… C_n', D_n' визначаються з умов на контурі. Навантаження на контурі повинно бути розкладено в тригонометричний ряд Фур’є за синусами та косинусами.

За допомогою функції напружень (5.16), додаючи при потребі ступеневі поліноми, можна отримати розв’язок для більш широкого кола задач, ніж за допомогою тільки ступеневих поліномів. Серед них можна назвати задачу про згин балки-стінки, задачу про дію на пластинку навантажень, розподілених вздовж контуру за будь-яким законом (в тому числі зосередженої сили).

Читайте також:

1. VII. Нахождение общего решения методом характеристик
2. А .Маршалл - основоположник неокласичної теорії.
3. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
4. Алгоритм розв’язання задачі
5. Алгоритм розв’язання розподільної задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі
10. Алгоритм розв’язування задачі
11. Алгоритм розв’язування задачі
12. Алгоритм розв’язування задачі оптимізації в Excel

Переглядів: 631