• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Основні визначення

Лекція № 14. ДЕРЕВА

Дерево – зв'язний граф без циклів. Ліс (або ациклічний граф) – неограф| без циклів. Компонентами лісу є|з'являються,являються| дерева.

Теорема 14.1. Для неографа| G з|із| n вершинами без петель наступні|слідуючі| умови еквівалентні:

1) G – дерево;

2) G – зв'язковий граф, що містить|утримує| n – 1 ребро;

3) G – ациклічний граф, що містить|утримує| n – 1 ребро;

4) Будь-які дві неспівпадаючі вершини графа G сполучає|поєднує,з'єднує| єдиний ланцюг|цеп|;

5) G – ациклічний граф, такий, що якщо в нього додати|добавити| одне ребро, то в ньому з'явиться|появиться| рівно один цикл.

Теорема 14.2. Неограф G є|з'являється,являється| лісом тоді і тільки|лише| тоді, коли коранг| графа v(G)=0.

Висяча вершина в дереві – вершина ступеня|міри| 1. Висячі вершини називаються листям, всі інші – внутрішніми вершинами.

Якщо в дереві особливо виділена одна вершина, звана коренем, то таке дерево називається кореневим, інакше – вільним.

Кореневе дерево можна рахувати орграфом| з|із| орієнтацією дуг з|із| кореня або в корінь. Очевидно, що для будь-якої вершини кореневого дерева, окрім|крім| кореня, . Для кореня: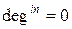, для листя: .

Вершини дерева, видалені|віддалені| на відстань k (у числі дуг) від кореня, утворюють k -й| ярус (рівень) дерева. Найбільше значення k називається висотою дерева.

Якщо з|із| якої-небудь вершини кореневого дерева виходять дуги, то вершини на кінцях цих дуг називають синами (у англійській літературі – дочки (daughter)).

Читайте також:

1. I визначення впливу окремих факторів
2. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
3. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
4. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
5. Ocнoвнi визначення здоров'я
6. Адвокатура в Україні: основні завдання і функції
7. Алгебраїчний спосіб визначення точки беззбитковості
8. Амортизація основних засобів, основні методи амортизації
9. Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
10. Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
11. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
12. Артеріальний пульс, основні параметри

Переглядів: 440