• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Закон її сумісного розподілу визначають за формулою

Таблиця 3.1

Хі Yі	х1	х2	...	хп
y1	p11	p21	…	pn1
y2	p12	P22		Pn2
…	…	…	…	…
ym	p1m	p2m		Pnm

Всі можливі події (X = x_i; Y = y_j) при і = і j = складають повну групу несумісних подій і тому

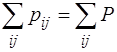(X = x_i, Y = y_j) = 1. (3.1)

§ 2. Система двох випадкових величин

Функцією розподілу системи двох випадкових величин називають функцію двох аргументів F(x,y), що дорівнює ймовірності сумісного виконання двох нерівностей X < x i Y < y, тобто

F(x,y) = P(X < x i Y < y). (3.2)

Геометрично функцією розподілу системи двох випадкових величин є ймовірність попадання випадкової точки (Х,Y) в нескінченний квадрат площини (рис.3.1) з вершиною в точці (х,у).

Функція розподілу має такі властивості:

1. Якщо один із аргументів наближається до плюс нескінченності, то функція розподілу системи наближається до функції розподілу випадкової величини другого аргументу, тобто

F (x, +¥) = F₁(x);

F (+¥, y) = F₂(y).

2.Принаближенні обох аргументів до плюс нескінченності функція розподілу F (x,y)наближається до одиниці:

, або F (+¥, +¥) = 1.

3. При наближенні одного чи обох аргументів до мінус нескінченності функція розподілу наближається до нуля:

,

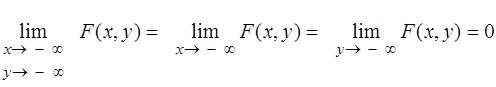або F (- ¥, у) = F ( х, - ¥) = F (- ¥, - ¥) = 0.

4. Функція розподілу (F (х, у)є зростаючою функцією з кожного аргументу:

F ( x₂, y) ³ F (x₁, y), якщо х₂ > x₁;

F ( x, y₂) ³ F (x, y₁), якщо у₂ > у₁.

5. Ймовірність попадання випадкової точки (х,у) в будь-який прямокутник зі сторонами, паралельними координатним осям, обчислюється за формулою

F ( x₂, y₂) - F ( x₁, y₂) -

-F ( x₂, y₁) + F ( x₁, y₁).(3.3)

Це легко з’ясувати геометрично, якщо уявити положення прямокутника з координатами вершин А( x₁, y₁), В( x₁, y₂) , С( x₂, y₂) і D( x₂, y₁) на рис.3.1 і геометричними значеннями функцій F( x₂, y₂), …, F( x₁, y₁)в формулі (3.3).

Практичне значення мають системи неперервних випадкових величин, розподіл яких характеризують щільністю розподілу j(x, y). За допомогою неї більш просто знаходять імовірність попадання в різні області, а опис розподілу системи випадкових величин стає більш наочним.

Щільність розподілу системи двох випадкових неперервних величин визначаютьяк другу змішану часткову похідну від функції F(x,y),тобто

j(х,у) = 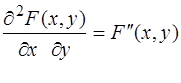. (3.4)

Геометрично функцію j(х,у)можна виразити просторовою поверхнею, що нагадує перевернутий до низу дзвоник, краї якого віддаляються до нескінченності, асимптотично наближаючись до площини х0у(рис.3.2). Її називають поверхнею розподілу.

Рис.3.1

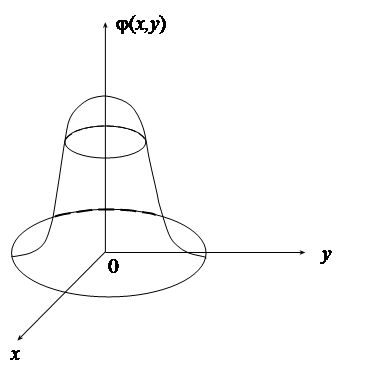
Рис.3.2

Функція розподілу F(x,y) визначається за формулою

F(x,y)= 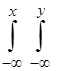j(x,y) dxdy. (3.5)

Щільність розподілу системи двох випадкових величин має властивості:

1. Щільністю розподілу є функція

j(x,y) ³ 0.

2. Подвійний інтеграл з нескінченними межами від функції щільності розподілу дорівнює одиниці:

j(x,y) dxdy = 1.

Геометрично це свідчить про те, що об’єм тіла, відмежованого поверхнею розподілу і площиною х0у, дорівнює одиниці.

Щільності розподілу величин х та у, що входять в систему, визначають за формулами:

j₁(х) = j(x,y) dy ;

j₂ (у) = j(x,y) dх .

Тобто, для визначення щільності розподілу однієї із системи випадкових величин, треба проінтегрувати в необмежених межах щільність розподілу системи j(х,у)за аргументом другої випадкової величини.

Якщо відомі щільності розподілу окремих випадкових величин системи і випадкові величини х та унезалежні між собою, то можна визначити закон їх сумісного розподілу за формулою

j(х,у) = j₁(х) × j₂ (у).

Подібно умовній імовірності Р для подій визначають умовні щільності розподілу:

1) j 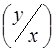-щільністьрозподілу y при умові, що випадкова величина Х прийняла значення х;

2) j 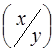- щільність розподілу х при умові, що випадкова величина Y прийняла значення у.

Закон її сумісного розподілу визначають за формулою

j(х,у) = j₁(х) j ,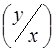

або j(х,у) = j₂(y) j .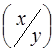

Поняття залежності та незалежності випадкових величин має велике значення в теорії ймовірностей та при математичній обробці результатів вимірів.

Випадкова величина Х буде незалежною від випадкової величини Y, якщо закон розподілу величини Х не залежить від прийнятого значення величини Y, тобто

j 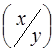= j₁(х),

і навпаки, для випадкової величини Y маємо

j 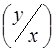= j₂(у).

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. II. Закон кийка та ікла
3. II. Найважливіші проблеми, що визначають розвиток місцевого самоврядування і є спільними для будь-яких урядових систем.
4. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
5. III етап. Аналіз факторів, що визначають цінову політику підприємства.
6. III закон Ньютона
7. IV. Закони ідеальних газів.
8. IV. Закономірності структурно-функціональної організації спинного мозку
9. IV. СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ І ЗАКОНОДАВСТВА.
10. ReM – модифікований критерій Рейнольда, який визначається за формулою
11. VII розділ. Маркетингові рішення з розподілу та збуту товару
12. А) Грошовий обіг. Закони.

Переглядів: 986