• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Якщо вони взаємно залежні між собою, то

j 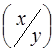¹ j₁(х);j 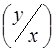¹ j₂(у).

Випадкові величини Х i Y незалежні, якщо щільність сумісного розподілу j(х,у)можна визначити у вигляді добутку двох множників, кожен із яких утримує тільки величини х та у, тобто

j(х,у) = .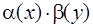

Додамо, що при розкладанні, функції 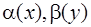з точністю до постійної множників збігаються з щільностями розподілу j₁(x) і j₂(у).

Між випадковими величинами виникає функціональна або стохастична (ймовірна)залежність.

Функціональною залежністю між випадковими величинами Х і Yназивають таку залежність, коли кожному значенню Х відповідає точне значення Y.

Наприклад, у = х², S = a×b і т.д.

Стохастичною (ймовірною) залежністю між випадковими величинами Х і Y називають таку залежність, при якій кожному значенню х можна вказати розподіл величини у, яке змінюється при зміні х.

Така залежність в практичній діяльності зустрічається досить часто. Наприклад, зріст та вага людини, висота і товщина дерева в лісі, величина деформації інженерних споруд, час їх експлуатації і т.д.

Тобто у випадку ймовірної залежності на кожне точне значення аргументу х можна вказати значення випадкової величини уз певною мірою ймовірності (Р_у).

Система двох випадкових величин може підкорятися різним законам розподілу. Проте в практиці геодезичних вимірювань найбільше розповсюдження має нормальний закон розподілу.

Якщо випадкові величини Х і Y мають нормальний розподіл і незалежні між собою, то щільності розподілу кожної із них будуть:

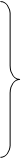j₁(х)= ;

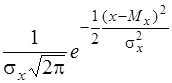(3.6)

j₂ (y ) = .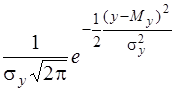

Згідно з формулою (2.69) щільність розподілу системи (Х, Y), якщо випадкові величини Х та Y незалежні, отримаємо у вигляді

j(х,у) = . (3.7)

Якщо центр системи (х,у) знаходиться на початку системи координат х0у, тобто М_х = М_у = 0, то

j(х,у)=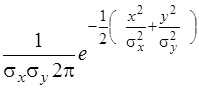. (3.8)

Поверхня щільності нормального розподілу системи (х,у) має опуклий вигляд (горб), показаний на рис.3.2.

Ймовірність попадання випадкової точки в прямокутник із сторонами паралельними осям координат, в межі з координатами х₁,х₂іу₁,y₂ (рис.3.1) визначається за формулою

Р(х₁ < X < x₂ , y₁ < Y < y₂) = 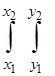j(x,y) dx dy. (3.9)

При нормальному розподілі системи двох випадкових величин отримаємо

Р(х₁ < X < x₂ , y₁ < Y < y₂) = 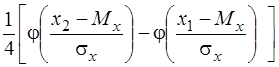´ ´ 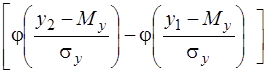. (3.10)

Приклад 1. Щільність розподілу системи двох випадкових величин (Х,Y) визначається за формулою

j(х,у) =.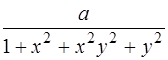

Знайти: а) значення а; б) функцію розподілу; в) визначити залежність випадкових величин X іY.

Розв’язання. а) Згідно з 2-ою властивістю щільності розподілу маємо

=

= .

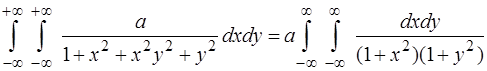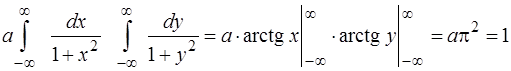Тоді ;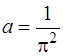

б) за формулою (2.68) отримаємо

;

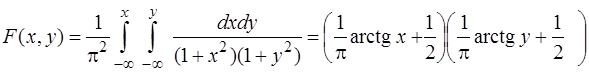в) при відомому значенні 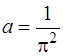функція щільності дорівнює

j(х,у) = .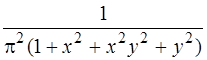

Читайте також:

1. Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
2. Безрозмірною характеристикою гідротрансформатора називається залежність коефіцієнтів пропорційності моментів насосного і турбінного коліс від його передаточного відношення.
3. Боротьба за возз’єднання Української держави, за незалежність у 60- 80-х роках XVII ст.
4. Боротьба за возз’єднання Української держави, за незалежність у 60-80-х роках XVII ст.
5. Вартість та залежність між величинами: ціна, кількість, вартість
6. Вектори є уже лінійно залежні.
7. Взаємно однозначні відповідності
8. Взаємозалежні
9. Взаємозалежність еластичності попиту від доходу, частки витрат на певний товар у загальних витратах Домогосподарств і обсягу попиту
10. Взаємозалежність і співвідношення громадянського суспільства і правової держави.
11. Взаємозалежність і співвідношення громадянського суспільства і правової держави.
12. Взаємозалежність між рівнем соціально-економічного розвитку суспільства і державно-правовими інститутами.

Переглядів: 972