• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Її можна розкласти на множники, тобто

j(х,у) =.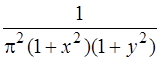

Це свідчить про те, що випадкові величини Х і Y незалежні. Тоді

; .

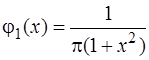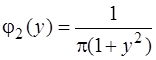Приклад 2. Визначити ймовірність попадання точки в прямокутник з координатами: х₁ = 1; х₂ = 3; y₁ = 2; y₂ = 4, якщо щільність розподілу системи випадкових величин (X,Y) підпорядковується нормальному закону з центром розсіювання в точці 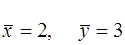і стандартом s_х = s_у = 0,5.

Розв’язання. Згідно з формулою (3.10) маємо

Р(х₁ < X < x₂ , y₁ < Y < y₂) = ´ ´ = .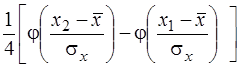

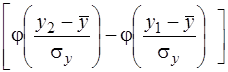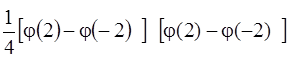За таблицею функцій Лапласа (дод.1) знаходимо j(2) = 0,95; j(-2) = -0,95.

Тоді Р = (0,95 + 0,95) (0,95 + 0,95) = 0,9.

§ 3. Числові характеристики системи двох випадкових величин. Кореляційний момент, коефіцієнт кореляції і рівняння регресії

Найбільш повними ймовірними характеристиками системи двох випадкових величин є закон розподілу. Однак в практичній діяльності не завжди є можливість визначити його. Тому при дослідженнях систему двох випадкових величин характеризують їх числовими характеристиками: початковими та центральними моментами.

Початковим моментом 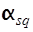порядку s, q системи (Х,Y) називається математичне сподівання від добутка Х^S на тобто

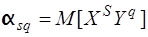. (3.11)

Для системи дискретних випадкових величин

, (3.12)

де Рx_iy_i = Р(Х = х_і; Y = y_i ) - ймовірність того, що система (х,у) прийме значення (х_і,у_і),адодавання розповсюджується по всіх можливих значеннях випадкових величин Хі Y.

Читайте також:

1. Internet. - це мережа з комутацією пакетів, і її можна порівняти з організацією роботи звичайної пошти.
2. А є А, тобто усякий предмет є те, що він є.
3. Адміністративні методи управління можна умовно поділити на організаційні та оперативно-розпорядчі.
4. Броунівський рух зовсім хаотичний, тобто в ньому спостерігається повна рівноправність всіх напрямків.
5. Важливе місце при цьому приділялося так званій «сімейній дипломатії», тобто укладенню вигідних союзів і угод шляхом династич­них шлюбів.
6. Важливою ознакою класифікації є принцип побудови перетворювачів кодів, згідно з яким їх можна поділити на чотири групи.
7. Види кредиту можна класифікувати за різними критеріями.
8. Видно, що ,( тобто площина паралельна до осі Ox.
9. Визначення очікування індивіду, тобто уявлення індивіду про те, що повинно відбутись.
10. Визначити ООП можна і багатьма іншими способами.
11. Вимірювання можна класифікувати за багатьма ознаками.
12. Випробування можна проводити у лабораторіях і в реальних умовах як на моделях, так і на реальних об'єктах

Переглядів: 418