• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Для системи неперервних випадкових величин

j(х,у) dx dy,(3.13)

де j(х,у)-щільність розподілу системи двох випадкових величин Х та Y.

В практичній діяльності найчастіше використовують початкові моменти першого порядку при s = 1, q = 0 і s = 0, q = 1згідно з формулами (3.11) і (2.15):

;(3.14)

. (3.15)

Як видно із формул (3.14) і (3.15) початковими моментами першого порядку будуть математичні сподівання випадкових величин Х і Y. Вони визначають координати точки, яку називають центром розсіювання системи (Х, Y)на площині.

Центральним моментом m_sqпорядку s,q системи (Х, Y) називається математичне сподівання добутку центрованих величин (Х – М_x) і (Y – M_y) відповідно в s-му і q-му степенях.

m_sq = М [(X – M_x)^S (Y – M_y)^q ]. (3.16)

Для системи дискретних і неперервних величин отримаємо:

m_sq= 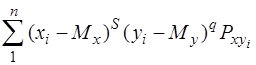;(3.17)

m_sq= j(х,у) dx dy. (3.18)

Практичне значення мають центральні моменти другого порядку при s = 2 і q = 0 та s = 0 і q = 2:

m₂₀ = М [(X – M_x)² (Y – M_y)⁰ ] = М [(X – M_x)²] = D_x; (3.19)

m₀₂ = М [(X – M_x)⁰ (Y – M_y)² ] = М [(Y – M_y)²] = D_y. (3.20)

Як видно вони є дисперсіями випадкових величин Х та Y і характеризують розсіювання випадкової точки з координатами (х, у) в напрямку осей 0хі 0y.

При дослідженнях системи випадкових величин важливу роль має змішаний центральний момент першого порядку -m₁₁. Його називають кореляційним моментом K_ху або моментом зв’язку і визначають за формулою

m₁₁ = K_ху = М [(X – M_x) (Y – M_y)].(3.21)

Для системи дискретних та неперервних величин його визначають за формулами

; (3.22)

K_ху= j(х,у) dx dy. (3.23)

В § 2 цього розділу показано, що між випадковими величинами Х і Y може виникати зв’язок. Кореляційний момент K_ху і характеризує силу або щільність зв’язку. Відомо, якщо між випадковими величинами існує ймовірний зв’язок (залежність), то зі зміною випадкової величини Х змінюється закон розподілу випадкової величини Y. В той же час закон розподілу задають кривою розподілу у = f(x). Характер кривих може бути різним, тому і відрізняють декілька типів імовірної залежності. Одним із найбільш розповсюджених типів є кореляційна залежність, за якої заміна аргументу х призводить до зміни математичного сподівання величини y (рис.3.3). В першому випадку (рис.3.3,а) ми маємо прямолінійну кореляцію, а на рис.3.3,б – криволінійну. При дослідженнях можуть виникнути й інші типи кореляційної залежності.

а б

Рис.3.3

Кореляційну залежність часто називають кореляцією. Як видно із формули (3.22) кореляційний момент має розмірність, яка залежить від розмірності випадкових величин Х і Y. Тому для оцінки сили зв’язку між випадковими величинами системи (Х, Y) використовують не коефіцієнт зв’язку K_ху, а безрозмірне відношення

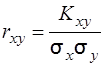, (3.24)

яке називають коефіцієнтом кореляції випадкових величин Х і Y.

Коефіцієнт кореляції змінюється в межах від -1 до +1, тобто

.

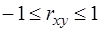Якщо r > 0, то маємо позитивну кореляцію, тобто із збільшенням абсциси x, збільшується величина ординати y (рис.3.3,а) і навпаки при r < 0 .

Якщо випадкові величини Х і Y незалежні, то кореляційний момент і коефіцієнт кореляції дорівнює нулю, тобто K_ху = 0 і r_xy = 0.

Дві корельовані випадкові величини завжди є взаємозалежними, але дві залежні величини не завжди є корельованими. Прикладом цього може бути система випадкових величин (Х, Y) рівномірно розподілена в межах кола з центром на початку координат. Розрахунки показують, що величини Х і Y залежні, а кореляційний момент K_ху = 0, а це означає, що і r_xy = 0 [15, с.125].

Випадкові величини Х і Y називають корельованими, якщо | r_xy| > 0 і при r_xy = 0 – некорельованими.

Коли коефіцієнт кореляції дорівнює +1 чи -1, то між величинами Х і Y існує прямолінійна залежність у вигляді рівняння прямої

у = ах + b.

Форма прямолінійного зв’язку між випадковими величинами Х і Y визначається у вигляді рівняння регресії Y на Х:

у = М_y+(х – М_x), (3.25)

і Х на Y

x = М_x + ( y – М_y). (3.26)

Коефіцієнти регресії і визначають за формулами

;, (3.27)

де значення r, s_x, s_y обчислюють за формулами (2.28), (3.24).

Приклад 1. Для системи випадкових величин (х₁=1;х₂ = 2; х₃ = 3; х₄ = 4; у₁ = 0,8; у₂ = 2,1; у₃ = 2,7; у₄ = 4,2) при ймовірностях їх появи = 0,25; 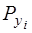= 0,25 знайти:

а) початкові моменти першого порядку при s = 1, q = 0is = 0, q= 1;

б)центральні моменти приs = 2, q = 0is = 0, q = 2;

в) обчислити кореляційний момент K_ху та коефіцієнт кореляції r_xy;

г) знайти рівняння регресії Y та Х.

Розв’язання. а) Початковими моментами величин Хта Y будуть їх математичні сподівання. За формулами (3.14), (3.15) та (2.15) обчислюємо:

α₁₀ = М_x = = 1 × 0,25 + 2 × 0,25 + 3 × 0,25 + 4 × 0,25 = 2,5;

α₀₁ = М_y = = 0,8 × 0,25 + 2,1 × 0,25 + 2,7 × 0,25 + 4,2 × 0,25 = 2,45.

б) Центральні моменти при s = 2, q = 0 i s = 0, q = 2обчислюють за формулами (3.19), (3.20) та (2.27):

m₂₀ = D_x = 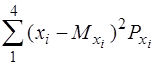= [(-1,5)² + (-0,5)² + (0,5)² + (1,5)²] ´ 0,25 = 1,25;

m₀₂ = D_y = 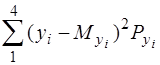= [(-1,65)² + (-0,35)² + (0,25)² + (1,75)²] 0,25 = 1,46.

в) Для визначення кореляційного моменту за формулою (3.22) обчислимо ймовірності прийняття системою (х, у) значень (х_і, у_і). Так як випадкові величини Х та Y з'являються одночасно і мають однакові значення ймовірностей = 0,25 і 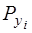= 0,25, то за формулою добутку ймовірностей маємо

= × .

Тоді

m₁₁ = K_ху=[(-1,5)(-1,65) + (-0,5)(-0,35) +

+ 0,5 × 0,25 + 1,5 × 1,75] × 0,062 = 0,33.

В пункті б) знайдено D_xі D_y, тоді стандарти будуть дорівнювати:

= 1,1; = 1,2.

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. POS-системи
8. T. Сутність, етіологія та патогенез порушень опорно-рухової системи
9. VI. Філогенез нервової системи
10. А) Заробітна плата її форми та системи.
11. А) Заробітна плата, її форми та системи.
12. А) оптимальне значення величини зварювального струму; б) підвищене значення величини зварювального струму; в) низьке значення величини зварювального струму.

Переглядів: 700