• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Ймовірність появи однієї із декількох несумісних подій дорівнює сумі ймовірностей цих подій.

Якщо подія В складається із подій А₁, А₂, ..., А_п ,

то Р(В) = Р(А₁+ А₂+ ...+ А_п)=Р(А₁) + Р(А₂) + ...+ Р(А_п),(1.8)

або = . (1.9)

Доведення. Припустимо: М₁ – число випадків сприятливих події А₁;

М₂ – число випадків сприятливих події А₂;

...........................................................................

М_п – число випадків сприятливих події А_п;

N – число всіх можливих випадків випробувань.

Згідно з формулою (1.2) маємо ймовірність кожної із елементарних подій

Р(А₁)= ;Р(А₂)= ; ... ;Р(А_п)= 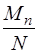.(1.10)

А₁, А₂, ..., А_п несумісні, тобто нема таких подій, що сприяють їх одночасній появі, то події Всприяють В = М₁ + М₂ + ...+ М_п випадків. Тоді

Р(В) = Р (А₁ + А₂ + .... + А_п)= .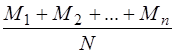

Згідно з формулами (1.10) отримаємо тотожність формулам (1.8; 1.9). Теорема доведена.

Із теореми додавання ймовірностей витікає два висновки.

Висновок 1. Якщо події А₁, А₂, ..., А_п утворюють повну групу несумісних подій, то сума їх імовірностей дорівнює одиниці

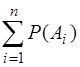= 1.(1.11)

Доведення. Так як події А₁, А₂, ... , А_п утворюють повну групу несумісних подій, то поява хоча б одного із них – достовірна подія, тоді

Р(А₁ + А₂ + .... + А_п) = Р(А₁) + Р(А₂) + ... + Р(А_п) = ,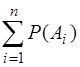

звідкілля 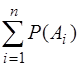= 1,

що і треба було довести.

Висновок 2. Сума ймовірностей двох протилежних подій дорівнює одиниці

Р(А) + Р( ) = 1 . (1.12)

Цей висновок витікає з висновку 1 і є його окремим випадком.

Приклад 2. На складі зберігається 100 теодолітів, із них: 20 – технічно справні, 76 – потребують перевірки та юстировки, решта – браковані. Знайти ймовірність того, що взятий навмання теодоліт можна використати в роботі.

Розв’язання. Це може статись при події А₁ – взято технічно справний теодоліт і події А₂ – взято теодоліт, який можна налагодити. Ймовірність цих подій дорівнює

Р(А₁) = = 0,20; Р(А₂) = = 0,76.

Так як ці події несумісні, то за формулою (1.8) знаходимо

Р(В) = Р(А₁) + Р(А₂) = 0,20 + 0,76 = 0,96.

Приклад 3. На топографічному плані є 80 пікетів, серед яких 6 бракованих. При контролі навмання вибирають 40 пікетів. Визначити ймовірність того, що план буде визнаний якісним, якщо допускається не більше двох бракованих пікетів серед перевірених.

Розв’язання. Позначимо через А – подію того, що при перевірці 40 пікетів не знайдеться жодного бракованого пікета, через В– подію, коли буде отримано тільки один бракований пікет і С – подію того, що буде отримано два бракованих пікети.

Події А, В і С несумісні. Згідно з умовами план буде прийнято, якщо виникне подія А + В + С. Тому за теоремою додавання ймовірностей і формулою (1.8) отримаємо

Р = Р(А) + Р(В) + Р(С).

Із 80-ти пікетів 40 можна вибрати способами, тобто N = . Із 74-х небракованих пікетів 40 пікетів можна вибрати 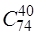способами, тобто М₁ = 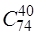. Тоді ймовірність події А за формулою (1.2) буде

Р(А) = .

Сприятливими подіями із бракованих 6-ти пікетів 1 бракований пікет може бути взятий 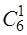способами, решта (40-1) пікетів не браковані і взяті із 74 пікетів 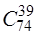системи. Тоді число сприятливих подій буде дорівнювати

М₂ = .

Отже Р(В) = .

Так само визначимо ймовірність події С

Р(С)= .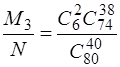

Тому Р = Р(А) + Р(В) + Р(С) = 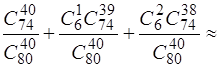0,34.

§ 5. Добуток подій. Теорема множення ймовірностей

Якщо подія S складається із А,В,С, ..., N простих подій, то може виникнути становище, коли вони всі разом сумісно з’являються.

Добуток S подій А, В, С, ..., N позначають так .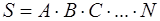

Приклад 1. Якщо подія А – є вірний результат виміру лінії; подія В – вірний результат виміру дирекційного кута, то подія С = визначає те, що вірними будуть і обчислені прирости координат Dхі Dу.

Перед розглядом теореми множення ймовірністей введемо поняття про залежні і незалежні події.

Подія А називається незалежною по відношенню до події В, якщо ймовірність події А не залежить від того, виникла подія В чи ні. В противному випадку подію А називають залежною від події В.

Приклад 2. При контролі знань студента викладач бере відлік по шкалі приладу після того, як відлік взяв студент. Імовірність помилки студента не залежить від помилки викладача і навпаки.

Декілька подій називають незалежними в сукупності, якщо кожна з них та будь-яка складна подія (складена із решти комбінацій всіх чи частки подій) – події незалежні.

Приклад 3. Якщо для вимірювання кута за інструкцією треба виконати два прийоми, то подія правильного виміру кута після другого прийому залежна, так як вона може виникнути лише за умови правильного вимірювання кута в першому прийомі.

Умовною ймовірністю називають імовірність, обчислену в передбаченні того, що одна чи декілька подій уже виникли.

Математично умова залежності події А від події В записується у вигляді

Р Р(А), (1.13)

а умова незалежності – у вигляді

Р 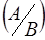= Р(А). (1.14)

На відміну від умовної ймовірності, ймовірність незалежних подій інколи називають безумовною ймовірністю.

Множення ймовірностей визначають теоремою: ймовірність множення двох чи декількох подій дорівнює множенню ймовірності однієї з них на умовні ймовірності решти подій, розрахованих у передбаченні, що всі попередні події мали місце.

Тобто

Р(А₁,А₂, ..., А_п) = Р(А₁)Р ... Р , (1.15)

або

.

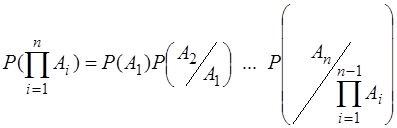Ймовірність множення двох подій дорівнює добутку ймовірності однієї з них на ймовірність другої, тобто

Р(АВ) = Р(А) Р = Р(В) Р 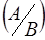. (1.16)

Із теореми множення ймовірностей витікає два висновки.

Висновок 1. Якщо подія А не залежить від події В, то і подія В не залежить від події А.

Доведення.Так як подія А не залежить від події В, то Р(А) = Р .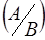

Читайте також:

1. А. Це наявність в однієї людини кількох ліній клітин з різним набором хромосом.
2. Алгебра випадкових подій
3. Алгебра подій
4. Алгебраїчна сума струмів у вузлі дорівнює нулю.
5. Алгоритми переведення чисел з однієї позиційної системи числення в іншу
6. Аналіз однієї ознаки
7. Безвілля, його заподій і переборення.
8. Види випадкових подій
9. Визначення базисних подій. Ідентифікація ризику.
10. Визначення добутку декількох множників
11. Визначте причини появи українського козацтва.
12. Визначте причини появи українського козацтва.

Переглядів: 623