
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
За теоремою множення ймовірностей маємо
Р(А) Р  = Р(В) Р
= Р(В) Р 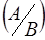 .
.
Згідно з умовою (1.16) отримаємо
Р(А) Р  =Р(В) Р(А).
=Р(В) Р(А).
Скоротимо на Р(А) і одержимо підтвердження висновку
Р  = Р(В).
= Р(В).
Тобто дві події незалежні тоді, коли поява однієї із них не змінить імовірності другої.
Висновок 2.Ймовірність незалежних подій в сукупності подій дорівнює множенню ймовірностей цих подій.
Тоді формула (1.15) буде
Р(А1×, А2× ,...,×Ап) = Р(А1) ×Р(А2) × ... ×Р (Ап), (1.17)
або
 . (1.18)
. (1.18)
Доведення. Для спрощення доказу візьмемо дві події А і В. Позначимо:
N1 – число всіх можливих випадків при випробуванні в яких з’явиться подія А;
N2 – число всіх можливих випадків при випробуванні в яких з’явиться подія В;
M1 – число сприятливих випадків події А;
М2 – число сприятливих випадків події В.
Загальна кількість можливих наслідків пар А і В, А і  ;
;  і В,
і В,  і
і  дорівнює N1 × N2.
дорівнює N1 × N2.
Число випадків, сприятливих сумісному виникненню подій А і В дорівнює М1 × М2. Тоді ймовірність сумісного виникнення подій А і В дорівнює
 .
.
Тобто Р(А×В) = Р(А) × Р(В). (1.19)
Якщо ймовірність всіх подій однакова, тобто Р(А1) = Р(А2) = ... = = Р(Ап)=Р,
то
Р (А1 А2 ... Ап) = Р п.(1.20)
Приклад 4. Вимір кута складаєтьсяіз ряду елементарних подій: А – центрування теодоліта, В – установка візирних цілей, С – візування зоровою трубою на візирні цілі, D – взяття відліку по лімбу горизонтального круга. Якщо ймовірності окремих подій дорівнюють Р(А) = 0,90; Р(В) = 0,95; Р(С) = 0,90; Р(D) = 0,99, то чому дорівнює ймовірність правильного виміру кута – Р(b) = ?
Розв’язання. Так як ймовірності подій А,В,С і D незалежні, і всі вони повинні з’явитися сумісно, то
Р(b) = Р(А) × Р(В) × Р(С) × Р(D),
тобто
Р(b) = 0,90 × 0,95 × 0,90 × 0,99 = 0,76.
§ 6. Теорема додавання ймовірностей сумісних подій
Якщо декілька подій за умовами випробування сумісні і подія виникає коли наступає хоча б одна із подій, то ймовірність її визначається теоремою:
Ймовірність появи хоча б однієї із двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх сумісного виникнення
Р(А + В) = Р(А) + Р(В) – Р(АВ),(1.21)
або
Р(А + В) = 1 – Р(  ) Р(
) Р(  ). (1.22)
). (1.22)
В загальному вигляді методом математичної індукції можна знайти
Р(А1+А2 + ... + Ап) = Р(А1) + Р(А2) + ... + Р(Ап) – Р(А1А2) –
– Р(А1А3) – ... – Р(Ап-1 Ап) + ... + (-1)п Р (А1А2 ... Ап), (1.23)
або
Р(В) = Р(А1 + А2 + ... + Ап) = 1 – Р(  .(1.24)
.(1.24)
Доведення. Розглянемо формулу (1.24). Найдемо зв’язок: протилежна подія  тотожна такому випадку, коли з’явиться хоча б одна протилежна подія
тотожна такому випадку, коли з’явиться хоча б одна протилежна подія 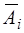 . Це можливо, якщо не з’явиться жодна подія Аі, що може бути коли одночасно з’являються всі протилежні події
. Це можливо, якщо не з’явиться жодна подія Аі, що може бути коли одночасно з’являються всі протилежні події  .
.
В цьому випадку застосуємо теорему множення, тоді
 .
.
Для незалежних подій
 . (1.25)
. (1.25)
Оскільки Р(В) + Р(  ) = 1, то від формули (1.25) переходимо до формули (1.24), що і треба було довести.
) = 1, то від формули (1.25) переходимо до формули (1.24), що і треба було довести.
Коли ймовірність подій Р(Аі) є рівною, то
Р(В) = 1 -  . (1.26)
. (1.26)
Приклад 1. З пунктів мостової тріангуляції двома різними методами виноситься центр опори моста. Ймовірність події першого методу дорівнює Р(А) = 0,90, а другого – Р(В) = 0,80. Знайти ймовірність перенесення центра опори моста з заданою точністю.
Розв’язання. Так як події А і Всумісні і незалежні, то ймовірність події С = А + В згідно з формулами (1.21) і (1.22) визначиться
Р(С) = 0,90 + 0,80 – 0,90 × 0,80 = 0,98;
Р(С) = 1 – 0,10 × 0,20 = 0,98.
Приклад 2. Кути мережі тріангуляції вимірювалися п’ятьма виконавцями. Ймовірність надійної роботи кожного дорівнювала Р(Аі) = 0,90. Яка ймовірність того, що нев’язки трикутників мережі будуть допустимими?
Розв’язання. Події вимірювання кутів кожним виконавцем робіт незалежні один від одного, але сумісні. Недопустима нев’язка з’явиться коли хоча б один із вимірів буде помилковим. Так як ймовірності кожного виміру кута однакові Р(Аі) = 0,90, то за формулою (1.26) знаходимо
Р(В) = 1 -  = 1 – 0,105 = 0,99995 » 1.
= 1 – 0,105 = 0,99995 » 1.
§ 7. Формула повної ймовірності. Теорема гіпотез
(формула Бейєса)
Припустимо, що цікава для нас подія А може настати (чи ні ) з однією із низки несумісних подій Н1, Н2, ..., Нп, що складають повну групу подій. Їх називають гіпотезами.
Якщо відомі ймовірності гіпотез Р(Н1), Р(Н2), ..., Р(Нп) і умовні ймовірності події А при здійсненні кожної гіпотези Ні, тобто Р 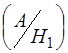 , Р
, Р 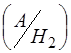 , ..., Р
, ..., Р 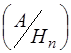 , то ймовірність події А визначається теоремою.
, то ймовірність події А визначається теоремою.
Ймовірність події А, що може виникнути разом з однією із гіпотез Н1, Н2, ..., Нп дорівнює сумі парних добутків ймовірностей кожної із цих гіпотез на відповідні їм умовні ймовірності появи події А:
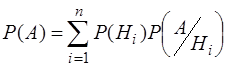 . (1.27)
. (1.27)
Її називають формулою повної ймовірності.
Доведення.Гіпотези Н1, Н2, ..., Нпутворюють повну групу подій. В цьому випадку подію А можна подати у вигляді додавання подій
А = АН1 + АН2 + ... + АНп =  .
.
Разом з тим події Нінесумісні, тоді і події АНі (  ) незалежні. Це дозволяє нам застосувати для визначення ймовірності події А теорему додавання ймовірностей несумісних подій (1.9). Тобто
) незалежні. Це дозволяє нам застосувати для визначення ймовірності події А теорему додавання ймовірностей несумісних подій (1.9). Тобто
 . (1.28)
. (1.28)
Ймовірність добутку подій А і Ні визначаємо за теоремою множення ймовірностей (1.16)
Р(АНі) = Р(Ні)Р  .
.
Підставимо цей вираз у формулу (1.28) і отримаємо


що і треба було довести.
Приклад 1. На складі зберігається 100 теодолітів з оптичним мікрометром, одержаних з трьох різних заводів відповідно: 40, 25 і 35 штук. Із числа приладів не потребують введення поправки за рен: 35 - першого, 20 - другого і 32 - третього заводу. Визначити ймовірність того, що взятий навмання прилад не потребує введення поправки за рен.
Розв’язання. Позначимо: Н1 – вибір приладу першого заводу; Н2 – другого заводу; Н3 – третього заводу; А – подія вибору приладу, що не потребує введення поправки за рен.
Знайдемо ймовірності гіпотез Н1, Н2 і Н3 за формулою (1.2)
Р(Н1) =  = 0,40; Р(Н2) =
= 0,40; Р(Н2) = 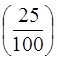 = 0,25і Р(Н3) =
= 0,25і Р(Н3) =  = = 0,35.
= = 0,35.
Обчислимо умовні ймовірності події А, що відображають вибір приладу, який не потребує введення поправки в рен. Для кожної із гіпотез Н1, Н2, Н3отримаємо
Р 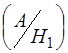 =
= 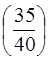 = 0,88;
= 0,88;
Р 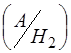 =
= 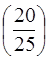 = 0,80;
= 0,80;
Р 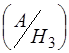 =
=  = 0,91.
= 0,91.
Знайдені ймовірності гіпотез Р(Н1), Р(Н2), Р(Н3)іумовних ймовірностей Р 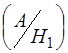 ,Р
,Р 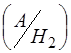 ,Р
,Р 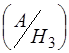 підставимо в формулу (1.27) і отримаємо
підставимо в формулу (1.27) і отримаємо
Р(А) = 0,40 · 0,88 + 0,25 · 0,80 + 0,35 · 0,91 = 0,87.
Аналогічно можна обчислити ймовірність того, що випадково взятий прилад потребує введення поправки за рен
Р(  ) = 0,40 · 0,12 + 0,25 · 0,20 + 0,35 · 0,09 = 0,13.
) = 0,40 · 0,12 + 0,25 · 0,20 + 0,35 · 0,09 = 0,13.
Розглянемо такий випадок. Є певна група несумісних подій Н1, Н2, ..., Нп. Відомі їх імовірності Р(Н1), Р(Н2), ..., Р(Нп).Після проведення дослідів з’явилася подія А, умовні ймовірності якої за кожною із гіпотез відомі і дорівнюють Р 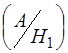 ,Р
,Р 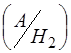 , ..., Р
, ..., Р 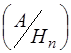 .
.
Виникає запитання:Якою буде ймовірність гіпотези Ні(  ) в зв’язку з появою події А?
) в зв’язку з появою події А?
Умовні ймовірності 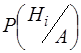 для кожної гіпотези визначають теоремою гіпотез.
для кожної гіпотези визначають теоремою гіпотез.
Ймовірність гіпотези після випробувань дорівнює добутку ймовірності гіпотези до випробувань на відповідну їй умовну ймовірність події, що з’явилась при проведенні досліду, поділеному на повну ймовірність цієї події
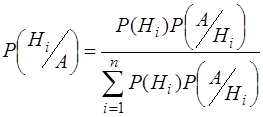 . (1.29)
. (1.29)
Її називають формулою Бейєса.
Доведення.Відповідно до формули (1.16) маємо
Р(А) 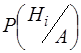 = Р(Ні)
= Р(Ні) 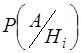 .
.
ЯкщоР(А)  0, то з цього рівняння маємо формулу Бейєса
0, то з цього рівняння маємо формулу Бейєса
 .
.
Виразимо Р(А) формулою (1.27) і отримаємо підтвердження теореми (1.29).
Приклад 2. В трьох теодолітних полігонах відповідно 20, 15 і 10 кутів. Серед них в першому полігоні 2, в другому – 1 і в третьому – 2 кути виміряні з недопустимою помилкою. Якщо при перевірці випадково взятий в журналі кут виявився помилковим, то яка буде ймовірність того, що він належить другому полігону?
Розв’язання. Визначимо через Н1, Н2іН3 гіпотези того, що випадково взятий кут відноситься до першого, другого і третього полігонів. Тоді ймовірності цих гіпотез при проведенні контролю рівні між собою, тобто
Р(Н1) = Р(Н2) = Р(Н3) =  .
.
Умовні ймовірності події появи помилкового кута за гіпотезами Н1, Н2,Н3 дорівнюють
 ;
;  і
і 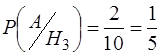 .
.
За формулою (1.29) знаходимо ймовірність гіпотези того, що випадково взятий кут буде із другого полігона
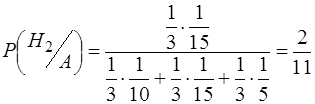 = 0,18.
= 0,18.
Якщо взятий кут виявиться правильним, то знайдемо, чому дорівнює ймовірність того, що цей кут буде із першого полігона?
В цьому випадку умовні ймовірності появи правильного кута за гіпотезами Н1, Н2 і Н3будуть дорівнювати
 ;
;  ;
;
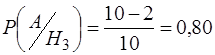 .
.
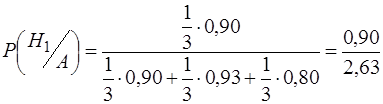 = 0,34.
= 0,34.
§ 8. Повторні випробування
При проведенні дослідів доводиться проводити багаторазові повторні випробування. Це найчастіше виникає при дослідженні нових геодезичних приладів, визначенні точності нових методів вимірювань. Слід підкреслити, що дослідження ведуть при додержанні встановленого комплексу умов.
Припустимо, що при проведенні декількох випробувань з’явиться подія А з визначеною ймовірністю р. Якщо ймовірність події А в кожному досліді не залежить від наслідків інших дослідів, то такі досліди будуть незалежними відносно події А.
Тоді виникає задача – знайти ймовірність того, що в результаті проведення пнезалежних випробувань подія А виникне m разів, якщо в кожному випробуванні ця подія з’являється з постійною ймовірністю Р(А) = Р.
Застосування теорем додавання та множення ймовірностей призводить до громіздких обчислень, особливо при великій кількості випробувань. Цю проблему вирішують за допомогою формули Бернуллі.
Виведення формули Бернуллі. Припустимо, що проведено п незалежних дослідів, результатом кожного може бути подія А з імовірністю Р(А) = p, або протилежна  з рівнем значності Р(
з рівнем значності Р(  ) = 1 –р = q. Так як комплекс умов не змінюється, то
) = 1 –р = q. Так як комплекс умов не змінюється, то
Р(А1) = Р(А2) = … = Р(Ап) = р;
Р( 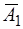 ) = Р(
) = Р( 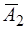 ) = ... = Р(
) = ... = Р( 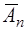 ) = q.
) = q.
Після першого випробування подія А може з’явитися чи не з’явитися, тобто можливі дві події, що утворюють повну групу: А,  .
.
Відомо, що сума ймовірностей подій, що утворюють повну групу подій, дорівнює одиниці, тоді
Р(А) + Р(  ) = 1,
) = 1,
або p + q = 1. (1.30)
Після двох незалежних подій виникнуть складні події: АА, А 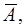
 А,
А, 
 .
.
Вони теж утворюють повну групу подій
Р(АА) + Р(А  ) + Р(
) + Р(  А) + Р(
А) + Р( 
 ) = 1. (1.31)
) = 1. (1.31)
Так як ці події незалежні, то за теоремою множення ймовірностей із формули (1.31) маємо
р2 + рq + qр + q2 = 1,
або (р + q)2 = 1. (1.32)
Методом математичної індукції за формулами (1.30) і (1.32) для трьох подій маємо:
(р + q)3 = 1. (1.33)
Аналогічні міркування для п дослідів приводять до висновку, що
(р + q)n = 1. (1.34)
Розкладемо біном (1.34) на суму ( п + 1) додатків, тоді

 , (1.35)
, (1.35)
де 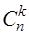 (k =
(k =  ) – біноміальні коефіцієнти; крім того
) – біноміальні коефіцієнти; крім того  =
= 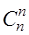 = 1.
= 1.
Аналіз формули (1.35) приводить до висновку, що перший член формули  виражає ймовірність того, що подія Аз’явиться 0 разів; другий член
виражає ймовірність того, що подія Аз’явиться 0 разів; другий член  – ймовірність того, що подія Аз’явиться 1 раз і т.д. Останній член формули
– ймовірність того, що подія Аз’явиться 1 раз і т.д. Останній член формули  – виражає ймовірність того, що подія А з'явиться п разів.
– виражає ймовірність того, що подія А з'явиться п разів.
Отже ймовірність того, що при п незалежних випробуваннях, коли ймовірність появи кожної події дорівнює р, сприятлива подія з'явиться k разів і визначається формулою
Рп(k) = 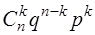 , (1.36)
, (1.36)
де Рп(k) – ймовірність появи події kразів при п випробуваннях;
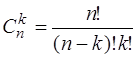 – число сполучень;
– число сполучень;
р– ймовірність появи події Ав одному випробуванні;
q – рівень значності події А в одному випробуванні.
Тоді
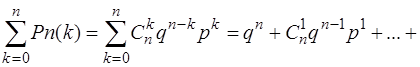
+ 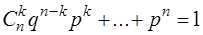 . (1.37)
. (1.37)
Так як члени формули (1.37) є членами розкладання бінома і одночасно визначають ймовірність появи події А при п випробуваннях ( п =  ),то сукупність ймовірностей Рп(k)називають біноміальним розподілом ймовірностей(k=
),то сукупність ймовірностей Рп(k)називають біноміальним розподілом ймовірностей(k= 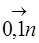 ).
).
При значеннях ni kбільше 10 розрахунки проводять з застосуванням формули Стирлінга
 . (1.38)
. (1.38)
Збіг суми членів (1.37) з членами розкладання бінома дозволяє ввести для обчислень ймовірностей можливого настання події А в серії п незалежних випробувань добуткову функцію jn(x):
jn(x) = (q + px)n = qnx0 +  qn-1px1 + … +
qn-1px1 + … +
+ 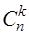 qn-k pk xk + …+ pn xn . (1.39)
qn-k pk xk + …+ pn xn . (1.39)
Ця функція характерна тим, що коефіцієнт при хk в розподіленні (1.39) дорівнює ймовірності появи події А рівноkразів в серії із п незалежних випробувань в перемінних умовах. Якщо ймовірність появи події А, що проходить в неоднакових умовах в і-му досліді дорівнює Р(Аі)=рі і рівень значності Р(  ) = qi, то ймовірність того, що подія А з’явиться рівно k разів в п незалежних випробуваннях буде дорівнювати коефіцієнту при хk в розподіленні за степенями хдобуткової функції
) = qi, то ймовірність того, що подія А з’явиться рівно k разів в п незалежних випробуваннях буде дорівнювати коефіцієнту при хk в розподіленні за степенями хдобуткової функції
jn (x) = (q1 + P1x) (q2 + P2x) …. (qn + Pnx). (1.40)
Приклад 1. Ймовірність виготовлення на автоматичному станку нівелірних рейок дорівнює 0,90. Знайти ймовірність того, що із 10-ти навмання взятих рейок 8 із них виявляться стандартними.
Розв’язання. Виготовлення рейок проводиться в однакових умовах. Тоді за формулою (1.36) при п=10, k = 8, р = 0,90, а q = 0,10 отримаємо
 =0,19.
=0,19.
Приклад 2. Знайти розподіл імовірностей числа прийомів виміру кута при чотирьох незалежних прийомах, якщо ймовірність виміру кута в одному прийомі дорівнює 0,9.
Розв’язання. За умовами п = 4, р = 0,9; q = 0,1. Використавши формулу (1.39), отримаємо
 (0,9 + 0,1х)4 = 0,14 х0 +
(0,9 + 0,1х)4 = 0,14 х0 + 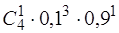 х1 +
х1 + 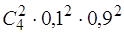 х2 +
х2 +
+  х4=0,0001х0 + 0,0036х1 + 0,0486х2 + 0,2916х3 + + 0,6561х4.
х4=0,0001х0 + 0,0036х1 + 0,0486х2 + 0,2916х3 + + 0,6561х4.
Шукані ймовірності є коефіцієнтами біля хk:
Р4(0) = 0,0001; Р4(1) = 0,0036; Р4(2) = 0,0486; Р4(3) = 0,2916;
Р4(4) = 0,6561.
Перевірка. 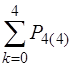 = 0,0001 + 0,0036 + 0,0486 + 0,2916 + 0,6561 = 1.
= 0,0001 + 0,0036 + 0,0486 + 0,2916 + 0,6561 = 1.
Як бачимо розв’язання вірне, а найбільш надійне число правильних прийомів виміру кута дорівнює чотирьом.
Приклад 3. Начальник партії, інспектор ВТК та головний інженер контролюють результати топографічної зйомки. Ймовірність виявлення браку для начальника партії дорівнює 0,8, інспектора ВТК – 0,9 і головного інженера – 0,6. Знайти ймовірність того, що два із них виявлять брак.
Розв’язання. Оскільки ймовірність для кожного контролюючого різна, тобто випробування проходять в різних умовах, то застосуємо добуткову функцію (1.40). Тоді при р1 = 0,8; р2 = 0,9; р3 = 0,6 і q1 = 0,2; q2 = 0,1; q3 = 0,4. Отримаємо:
j3(х) = (0,2 + 0,8х) (0,1 + 0,9х) (0,4 + 0,6х) = 0,008х0 + 0,272х1 +
+ 0,288х2 + 0,432х3.
Коефіцієнт біля х2є шуканою ймовірністю Р3(2) = 0,288.
Між іншим, маємо найбільшу ймовірність того, що троє перевіряючих знайдуть брак, так як Р4(3) = 0,432.
§ 9. Найбільш імовірне число появи подій при повторних випробуваннях
Припустимо, що випробування проводяться в однакових умовах. Незаперечно, якщо однакові ймовірності появи подій, то при повторних багатократних випробуваннях існує найбільш імовірне число появи події.
Визначення. Найбільш імовірним числом k появи події А в п незалежних випробуваннях буде число, для якого ймовірність Рп(k) перевищує чи, в крайньому разі, не менше ймовірності із решти можливих наслідків випробувань.
Приклад 1. Проведено 8 прийомів виміру кута. Ймовірність появи плюсової чи мінусової помилки однакова і дорівнює р = 0,5.
Знайти найбільш імовірне число появи плюсової помилки.
Розв’язання. Так як незалежні виміри іпроводяться в однакових умовах, то ймовірності появи будь-якого числа появи плюсової помилки можна знайти за формулою біноміального розподілу (1.35) або (1.39). Тоді при п = 8
Таблиця 1.1
| k | S | |||||||||
| Pn(k) | 0,004 | 0,031 | 0,109 | 0,219 | 0,273 | 0,219 | 0,109 | 0,031 | 0,004 | 1,000 |
Відповідно до табл.1.1 найбільша ймовірність Р = 0,273 буде супутньою для появи шуканої події при k = 4.
Разом з тим, якщо число випробувань п велике, то застосування формули біноміального розподілу буде складним.
Посилаючись на формулу (1.36) дещо спростимо розв’язання цієї задачі. Якщо в ряді багаторазових випробувань події є найбільш імовірним число k0появи цієї події, то повинні виконуватися нерівності
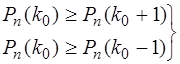 . (1.41)
. (1.41)
За допомогою формули (1.36) після розкриття членів отримаємо
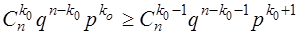 ,
,
або  .
.
Після скорочень отримаємо
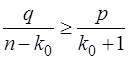 .
.
Розв’язавши цю нерівність відносно k0, отримаємо
k0 ³ np – q, (1.42)
так як (р + q) = 1.
Аналогічно із нерівності (1.41) отримаємо
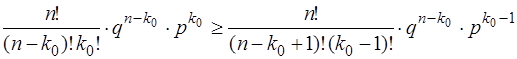 .
.
Після скорочення маємо
 ,
,
або
k0 £ np + p. (1.43)
Тоді за формулою (1.42) і (1.43) маємо подвійну нерівність, що служить для визначення найбільш імовірного числа k0
np – q £ k0 £ np +p. (1.44)
Довжина інтервалу появи числа k0 дорівнює одиниці. Тому якщо границі його є дробні числа, то маємо одне ціле число k0,а якщо цілі, то будемо мати два найбільші ймовірного числа подій – k0.
Приклад 2. При вимірюванні ліній теодолітних полігонів імовірність правильних вимірів окремих ліній дорівнює р = 0,90. Знайти найбільш імовірне число виміряних ліній, що відповідають вимогам точності, якщо в полігонах всього 150 ліній.
Розв'язання. За умовами прикладу п = 150,р = 0,90,q = 1 – p=0,10.Згідно з нерівностями (1.44) маємо
150×0,90 – 0,10 £ k0 £ 150×0,90 + 0,90,
звідкілля 134,9 £ k0 £ 135,9.
Отже, найбільш імовірне число правильно виміряних ліній буде дорівнювати 135.
Запитання для самоперевірки
1. Що вивчає теорія ймовірностей?
2. Дайте визначення подій. Наведіть приклади.
3. Які події називають випадковими?
4. Що таке комплекс умов?
5. Як ви розумієте повну групу подій? Наведіть приклад.
6. Що називають частотою події?
7. Приведіть класичне визначення ймовірності події. В яких межах змінюється ймовірність події?
8. Що таке принцип практичної впевненості?
9. При яких умовах виникає додавання і добуток складних подій?
10. Сформулюйте теореми додавання ймовірностей.
11. Які події називають залежними і незалежними?
12. Що таке умовна та безумовна ймовірність?
13. Сформулюйте теорему множення ймовірностей.
14. Сформулюйте теорему додавання ймовірностей для сумісних подій.
15. Напишіть формули повної ймовірності та ймовірності гіпотез (Бейєса).
16. В яких задачах виникає необхідність застосування формул повної ймовірності та ймовірності гіпотез?
17. Коли застосовують формулу Бернуллі?
18. Приведіть формулу появи k-oї події при п незалежних випробуваннях?
19. Напишіть формулу добуткової функції jп(х) настання події А в серії пнезалежних випробуваннях.
20. Який вигляд має добуткова функція ймовірностей появи подій, коли випробування проходять в неоднакових умовах?
21. Як визначити найбільш імовірне число появи подій при повторних випробуваннях?
Читайте також:
- II. Множення круглих багатоцифрових чисел на розрядні числа.
- А також для вегетативного розмноження.
- Аксіоми додавання і множення
- Асоціативний, або сполучний закон множення.
- Безстатеве розмноження та його біологічне значення
- Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
- Біологія розмноження тварин.
- Вегетативне розмноження
- Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
- Визначення добутку цілих невід’ємних чисел через суму. Операція множення цілих невід’ємних чисел
- Випадки множення і ділення в межах 1000, які зводяться до табличних. Розв'язання задач.
- Властивості ймовірностей
| <== попередня сторінка | | | наступна сторінка ==> |
| Ймовірність появи однієї із декількох несумісних подій дорівнює сумі ймовірностей цих подій. | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |