• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення добутку цілих невід’ємних чисел через суму. Операція множення цілих невід’ємних чисел

Розглянемо інший підхід до означення добутку цілих невід’ємних чисел, в основі якого лежить поняття суми.

Означення. Добутком цілих невід’ємних чисел а і b називається таке ціле невід’ємне число , яке задовольняє такі вимоги:

1) , якщо ;

2) , якщо ;

3) , якщо .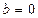

Теоретико-множинний смисл цього означення наступний. Якщо множини містять по а елементів кожна і ніякі дві з них не перетинаються, то їх об’єднання містить елементів. Отже, добуток - це число елементів в об’єднанні b множин, які попарно не перетинаються, кожна з яких містить по а елементів. Рівності і 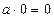приймаються за умовою, адже не можна сказати «а взяти доданком 1 раз» або «нуль раз».

Так, тільки на конкретних множинах вводять за діючими підручниками поняття добутку у другому класі. Перед учнями ставлять, наприклад, задачу: «У кожній парі по 2 вишні. Скільки всього вишень у шести парах?».

Записавши результат за допомогою суми 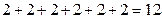(в.), з’ясовують, що такий запис суми дуже громіздкий і обчислення виконувати довго і незручно навіть при такій, порівняно невеликій, кількості доданків. А що коли б потрібно було визначити кількість вишень у 25 парах або 40? Тому умовились додавання однакових доданків вважати окремою дією – множенням – і записувати коротше: .

Після цього поступово складають таблицю множення (тобто множення одноцифрових чисел), яку діти заучують.

Дією, за допомогою якої знаходять добуток двох чисел а і b називають множенням, числа, які перемножують, - множниками, зокрема, число а називають множеним, а число b – множником, добутком називають вираз і результат множення.

Читайте також:

1. CMM. Визначення моделі зрілості.
2. I визначення впливу окремих факторів
3. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
4. II. Множення круглих багатоцифрових чисел на розрядні числа.
5. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
6. N – чисельність популяції
7. Ocнoвнi визначення здоров'я
8. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
9. VII. Професійна кооперація
10. А також для вегетативного розмноження.
11. А. Визначення розмірів і площі зони хімічного зараження.
12. Аксіома неперервності дійсних чисел

Переглядів: 4150