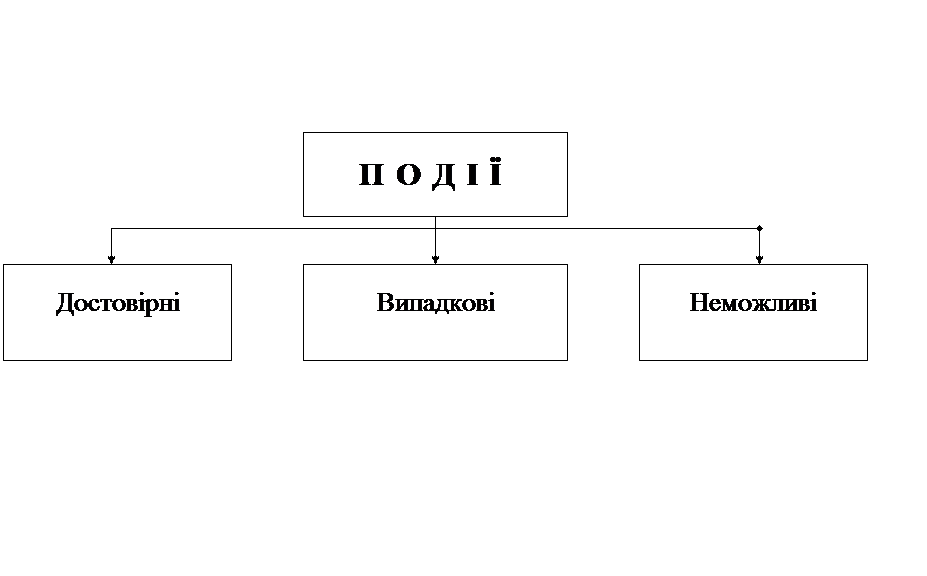
Види випадкових подій

Випробування і події

ТЕМА 1. ОСНОВНІ ПОНЯТТЯ ТЕОРІЇ ЙМОВІРНОСТЕЙ

Подію називають випадковою, якщо при здійсненні визначеної сукупності умов S вона може або відбутися, або не відбутися. Надалі замість того, щоб говорити "сукупність умов S здійснена", будемо говорити коротко: "зроблено випробування". Таким чином, подія буде розглядатися як результат випробування.

Приклад 1. Стрілець стріляє по мішені, розділеній на чотири області. Постріл - це випробування. Влучення у визначену область мішені - подія.

Приклад 2. В урні знаходяться кольорові кулі. З урни навмання беруть одну кулю. Виймання кулі з урни є випробування. Поява кулі визначеного кольору - подія.

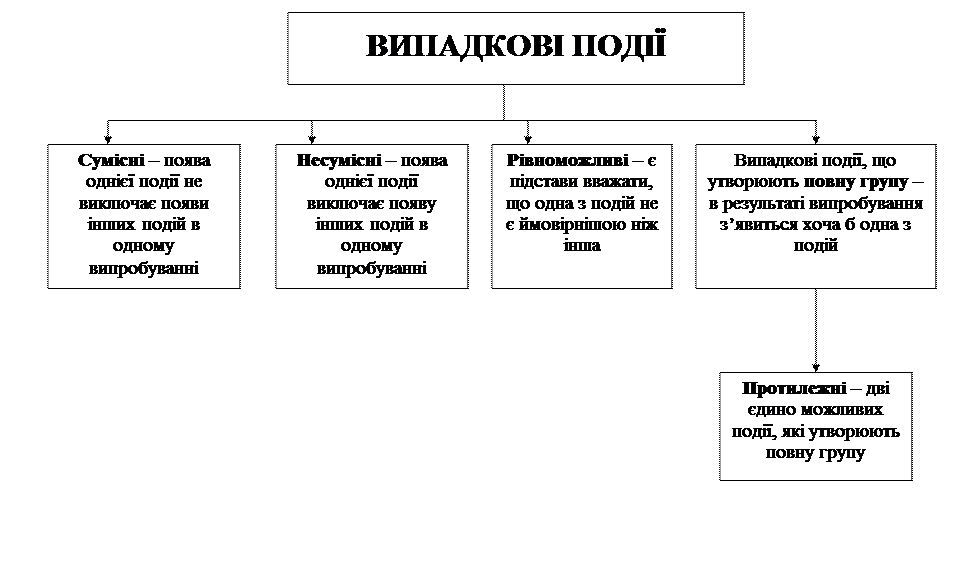
Події називають несумісними, якщо поява однієї з них виключає появу інших подій у тому самому випробуванні.

Приклад 1. Із ящика з деталями навмання вийнята деталь. Поява стандартної деталі виключає появу нестандартної деталі. Події "з’явилася стандартна деталь" і "з’явилася нестандартна деталь" - несумісні.

Приклад 2. Кинуто монету. Поява "герба" виключає поява надпису. Події "з’явився герб" і "з’явився надпис" - несумісні.

Кілька подій утворять повну групу, якщо в результаті випробування з’явиться хоча б одна з них. Іншими словами, поява хоча б однієї з подій повної групи є достовірна подія. Зокрема, якщо події, що утворюють повну групу, попарно несумісні, то в результаті випробування з’явиться одна і тільки одна із цих подій. Цей окремий випадок представляє для нас найбільший інтерес, оскільки використовується далі.

Приклад 3. Придбано два квитки грошово-речової лотереї. Обов’язково відбудеться одна і тільки одна з наступних подій: "виграш випав на перший квиток і не випав на другий", "виграш не випав на перший квиток і випав на другий", "виграш випав на обидва квитки", "на обидва квитки виграш не випав". Ці події утворять повну групу попарно несумісних подій.

Приклад 4. Стрілець зробив постріл по цілі. Обов’язково відбудеться одна з наступних двох подій: влучення, промах. Ці дві несумісних події утворять повну групу.

Події називають рівноможливими, якщо є підстави вважати, що жодна з них не є більш можливою, ніж інша.

Приклад 5. Поява "герба" і поява надпису при киданні монети - рівноможливі події. Дійсно, передбачається, що монета виготовлена з однорідного матеріалу, має правильну циліндричну форму і наявність карбування не чинить впливу на випадання тієї чи іншої сторони монети.

Приклад 6. Поява того чи іншого числа очок на кинутій гральній кістці – рівноможливі події. Дійсно, передбачається, що гральна кіста виготовлена з однорідного матеріалу, має форму правильного багатогранника і наявність очок не робить впливу на випадання будь-якої грані.

1.2. Операції над подіями

При розробці апарату і методики дослідження випадкових подій в теорії ймовірностей дуже важливим є поняття суми і добутку подій.

Сумою, або об’єднанням, декількох подій називається подія, що полягає в настанні хоча б однієї з цих подій.

Сума S подій А, В, С,..., N позначається так:

S = А +В + С+ ... +N

Наприклад, якщо подія А є влучення в ціль при першому пострілі, подія В - при другому, то подія С = А + В є влучення в ціль взагалі, байдуже, при якому пострілі - першому, другому або при обох разом.

Добутком, або перетином, декількох подій називається подія, що полягає в сумісній появі всіх цих подій.

Добуток S подій А, В, С..., N позначається

5 = АВС...N

Наприклад, якщо подія А є влучення в ціль при першому пострілі, подія В - при другому, то подія С = АВ полягає в тому, що в ціль влучили при обох пострілах.

Поняття суми і добутку подій мають наочну геометричну інтерпретацію. Хай подія А полягає в, попаданні точки в область А, подія В - в попаданні в область В, тоді подія А + В полягає в попаданні точки в область, заштриховану на рис. 1, і подія АВ - в попаданні точки в область, заштриховану на рис. 2.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
РОЗДІЛ 1. ВИПАДКОВІ ПОДІЇ	\|	Класичне визначення ймовірності

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.03 сек.