
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Класичне визначення ймовірності
Ймовірність - одне з основних понять теорії ймовірностей. Існує кілька визначень цього поняття. Приведемо визначення, що називають класичним. Далі вкажемо слабкі сторони цього визначення і приведемо інші визначення, що дозволяють перебороти недоліки класичного визначення.
Розглянемо приклад. Нехай в урні міститься 6 однакових, ретельно перемішаних куль, причому 2 з них - червоні, 3 - сині і 1 - біла. Очевидно, можливість вийняти навмання з урни кольорову (тобто червону чи синю) кулю більша, ніж можливість витягти білу кулю. Чи можна охарактеризувати цю можливість числом? Виявляється, можна. Це число і називають ймовірністю події (появи кольорової кулі).
Таким чином, ймовірність є число, що характеризує ступінь можливості появи події.
Поставимо перед собою завдання дати кількісну оцінку можливості того, що узята навмання куля кольорова. Появу кольорової кулі будемо розглядати як подію А. Кожний з можливих результатів випробування (випробування полягає у діставанні кулі з урни) назвемо елементарним результатом (елементарною подією). Елементарні події позначимо через 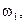
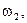
 і т.д. У нашому прикладі можливі наступні 6 елементарних результатів:
і т.д. У нашому прикладі можливі наступні 6 елементарних результатів: 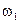 - з’явилася біла куля;
- з’явилася біла куля; 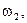
 - з’явилася червона куля;
- з’явилася червона куля; 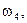

 - з’явилася синя куля. Легко бачити, що ці результати утворять повну групу попарно несумісних подій (обов’язково з’явиться тільки одна куля) і вони рівноможливі (кулю виймають навмання, кулі однакові і ретельно перемішані).
- з’явилася синя куля. Легко бачити, що ці результати утворять повну групу попарно несумісних подій (обов’язково з’явиться тільки одна куля) і вони рівноможливі (кулю виймають навмання, кулі однакові і ретельно перемішані).
Ті елементарні результати, у яких подія, що нас цікавить, настає, назвемо такими, що сприяють цій події. У нашому прикладі сприяють події А (появі кольорової кулі) наступні 5 результатів: 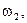

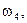

 .
.
Таким чином, подія А спостерігається, якщо в випробуванні настає один, байдуже який, з елементарних результатів, що сприяють А; у нашому прикладі А спостерігається, якщо наступить 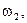 або
або  або
або 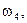 або
або  або
або  . У цьому розумінні подія А підрозділяється на кілька елементарних подій (
. У цьому розумінні подія А підрозділяється на кілька елементарних подій (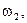

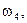

 ); елементарна ж подія не підрозділяється на інші події. У цьому полягає розходження між подією А і елементарною подією (елементарним результатом).
); елементарна ж подія не підрозділяється на інші події. У цьому полягає розходження між подією А і елементарною подією (елементарним результатом).
Відношення числа сприятливих події А елементарних результатів до їх загального числа називають ймовірністю події А і позначають через Р (А). У розглянутому прикладі усього елементарних результатів 6; з них 5 сприяють події А. Отже ймовірність того, що взята куля виявиться кольоровою, дорівнює Р (А) = 5/6. Це число і дає ту кількісну оцінку ступеня можливості появи кольорової кулі, що ми хотіли знайти. Дамо тепер визначення ймовірності.
Ймовірністю події А називають відношення числа сприятливих цій події результатів до загального числа всіх рівноможливих несумісних елементарних результатів, що утворюють повну групу.
Отже, ймовірність події А визначається формулою

де m - число елементарних результатів, що сприяють події А; n - число всіх можливих елементарних результатів випробування.
Тут передбачається, що елементарні результати несумісні, рівноможливі й утворюють повну групу. З визначення ймовірності випливають наступні її властивості:

Властивість 1. Ймовірність достовірної події дорівнює одиниці.
Дійсно, якщо подія достовірна, то кожен елементарний результат випробування сприяє події. У цьому випадку m=n, отже,

Властивість 2. Ймовірність неможливої події дорівнює нулю.
Дійсно, якщо подія неможлива, то жоден з елементарних результатів іспиту не сприяє події. У цьому випадку m = 0, отже,

Властивість 3. Ймовірність випадкової події є позитивне число, укладене між нулем і одиницею.
Дійсно, випадковій події сприяє лише частина з загального числа елементарних результатів випробування. У цьому випадку 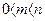 , отже виходить, що
, отже виходить, що 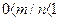 , отже,
, отже,
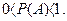
Отже, ймовірність будь-якої події задовольняє подвійній нерівності

Далі будуть приведені теореми, що дозволяють за заданими ймовірностями одних подій знаходити ймовірності інших подій.
Зауваження. Сучасні строгі курси теорії ймовірностей побудовані на теоретико-множинній основі. Обмежимося викладенням мовою теорії множин тих понять, що розглянуті вище.
Нехай у результаті іспиту настає одна і тільки одна з подій 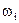

 ...
...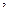
 Події
Події 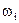 називають елементарними подіями (елементарними результатами). Уже звідси випливає, що елементарні події попарно несумісні. Безліч усіх елементарних подій які можуть з’явитися у випробуванні, називають простором елементарних подій
називають елементарними подіями (елементарними результатами). Уже звідси випливає, що елементарні події попарно несумісні. Безліч усіх елементарних подій які можуть з’явитися у випробуванні, називають простором елементарних подій  , а самі елементарні події - точками простору
, а самі елементарні події - точками простору  .
.
Подію А ототожнюють з підмножиною (простору  ), елементи якого є елементарні результати, що сприяють події А; подія В є підмножина
), елементи якого є елементарні результати, що сприяють події А; подія В є підмножина  , елементами якої є результати, що сприяють В, і т.д. Таким чином, множина усіх подій, що можуть наступити у випробуванні, є безліч усіх підмножин
, елементами якої є результати, що сприяють В, і т.д. Таким чином, множина усіх подій, що можуть наступити у випробуванні, є безліч усіх підмножин  . Саме
. Саме  настає при будь-якому результаті випробування, тому
настає при будь-якому результаті випробування, тому  - достовірна подія; порожня підмножина простору
- достовірна подія; порожня підмножина простору  - неможлива подія (вона не настає ні при якому результаті випробування).
- неможлива подія (вона не настає ні при якому результаті випробування).
Відмітимо, що елементарні події виділяються з числа всіх подій тим, що кожна з них містить тільки один елемент  .
.
Кожному елементарному результату 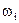 ставлять у відповідність позитивне число
ставлять у відповідність позитивне число 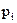 - ймовірність цього результату, причому
- ймовірність цього результату, причому  .
.
За визначенням, ймовірність  події
події 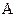 дорівнює сумі ймовірностей елементарних результатів, що сприяють події
дорівнює сумі ймовірностей елементарних результатів, що сприяють події 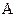 . Звідси легко отримати, що ймовірність достовірної події дорівнює одиниці, неможливої – нулю, довільної – знаходиться між нулем та одиницею.
. Звідси легко отримати, що ймовірність достовірної події дорівнює одиниці, неможливої – нулю, довільної – знаходиться між нулем та одиницею.
Розглянемо важливий частковий випадок, коли всі результати рівноможливі. Число результатів дорівнює 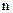 , сума ймовірностей всіх результатів дорівнює одиниці, значить ймовірність кожного результату дорівнює
, сума ймовірностей всіх результатів дорівнює одиниці, значить ймовірність кожного результату дорівнює 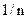 . Нехай події
. Нехай події  сприяє
сприяє 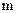 результатів. Ймовірність події
результатів. Ймовірність події  дорівнює сумі ймовірностей результатів, що сприяють
дорівнює сумі ймовірностей результатів, що сприяють  :
:
P(A)=1/n+1/n+…1/n.
З огляду на те, що число складових дорівнює 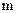 , маємо
, маємо
P(A)=m/n.
Отримано класичне визначення ймовірності.
Побудова логічно повноцінної теорії ймовірностей ґрунтується на аксіоматичному визначенні випадкової події і її ймовірності. У системі аксіом, запропонованій О.М. Колмогоровим, невизначуваними поняттями є елементарна подія і ймовірність. Приведемо аксіоми, що визначають ймовірність:
1. Кожній події А поставлено у відповідність невід’ємне дійсне число Р(А). Це число називається ймовірністю події А.
2. Ймовірність достовірної події дорівнює одиниці:
P ( ) =1.
) =1.
3. Ймовірність настання хоча б однієї із попарно несумісних подій дорівнює сумі ймовірностей цих подій.
Виходячи з цих аксіом, властивості ймовірностей і залежності між ними виводять в якості теорем.
Читайте також:
- I визначення впливу окремих факторів
- II. Визначення мети запровадження конкретної ВЕЗ з урахуванням її виду.
- II. Мотивація навчальної діяльності. Визначення теми і мети уроку
- Ocнoвнi визначення здоров'я
- Алгебраїчний спосіб визначення точки беззбитковості
- Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
- Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
- Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
- Балансова теорія визначення статі. Диференціація статі і роль гормонів у цьому процесі.
- Банкрутство підприємства: причини, оцінка ймовірності настання та наслідки
- Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
- Біостратиграфічні методи визначення віку порід
| <== попередня сторінка | | | наступна сторінка ==> |
| Види випадкових подій | | | Відносна частота. Стійкість відносної частоти |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |