• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Стислі теоретичні відомості

Седиментаційний аналіз – це метод визначення розмірів часток та фракційного складу дисперсних систем за допомогою безперервного зважування осаду.

На сферичну частку, що осідає у в’язкому середовищі, діють три сили: спрямована вниз сила тяжіння 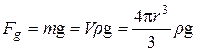та дві сили, спрямовані вгору: сила Архімеда 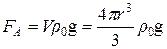і сила в’язкого опору (сила Стокса) . За умови рівноваги сил, що діють на частинку, вона рухається рівномірно та прямолінійно. Швидкість руху частинки можна визначити за рівнянням, що описує спільну дію трьох сил

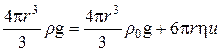
і після нескладних спрощень перетворюється на вираз:

,

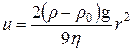(4.1)

де u – швидкість осідання частинки, м/с; r та 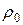– відповідно густина дисперсної фази та дисперсійного середовища, кг/м³; g – прискорення сили тяжіння, м/с²; – в’язкість дисперсійного середовища, Па·с; r – еквівалентний радіус сферичної частинки, м.

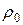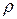Рівняння (4.1) можна використовувати для визначення розмірів часток дисперсної фази, що седиментує, якщо відомі характеристики дисперсійного середовища та і дисперсної фази , а також швидкість осідання часток 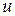, перетворивши його на формулу для розрахунків радіусів часток дисперсної фази:

.

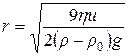(4.2)

Якщо в рівнянні (4.2) всі постійні за умови досліду величини об’єднати в одну константу 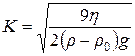, то воно набуває вигляду

.

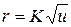(4.3)

Швидкість осідання часток можна визначити експериментально, якщо відомі висота 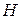та час 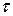їхнього осідання, як .

Знаючи 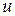та розрахувавши константу 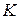, за рівнянням (4.3) можна обчислити еквівалентні радіуси часток, що осідають за певні інтервали часу.

Для полідисперсних систем седиментаційний аналіз проводять методом безперервного зважування осаду при седиментації. За даними, що одержані експериментально, будують седиментаційну криву – залежність маси часток 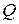, що осіли, від часу осідання τ. Потім експериментальну криву обробляють графічно для побудови диференціальної кривої розподілу часток за розмірами.

Розглянемо спочатку процес осадження монодисперсної суспензії, частки якої мають однакові розміри і осідають з рівними швидкостями. За однакової концентрації часток в кожній точці суспензії кількість частинок, що осідають за одиницю часу на шальку терезів, є незмінною, тому залежність 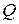від τ має лінійний вигляд (рис. 13). Точка B відповідає моменту закінчення осідання часток. Спочатку на шальки торсійних терезів (див. рис. 17) потрапляють частинки, що осідають з малої висоти. Останніми шальки терезів досягають частинки, що осідають з максимальної висоти 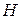(з поверхневого шару суспензії). Точка B на
рис. 13 відповідає часу 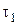, упродовж якого частинки долають відстань 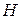. За цей час осядуть всі частинки суспензії, і подальшого накопичення осаду не відбуватиметься. Обчисливши 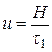, за рівнянням (4.3) можна визначити еквівалентний радіус часток.

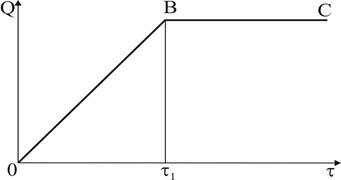
Рис. 13. Седиментаційна крива монодисперсної суспензії

Якщо суспензія є бідисперсною, тобто містить частинки тільки двох різних розмірів, то процес їх осадження можна розглядати як одночасне осадження двох монодисперсних фаз (рис. 14).

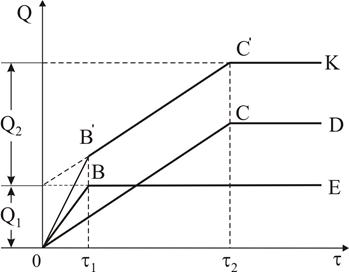
Рис. 14. Седиментаційна крива бідисперсної суспензії

Осідання фракції більших за розміром частинок описується прямою 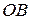, менших за розміром – прямою 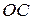; сумісне осідання обох фракцій описується лінією 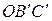, що є геометричною сумою 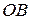та 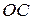. Точки зламу на лінії 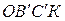відповідають моментам повного осідання великих (точка 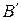, τ₁) та малих (точка 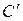, τ₂) частинок. За цими точками можна обчислити швидкості осідання частинок та 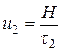і, відповідно, їх радіуси r₁ та r₂.

За кривою седиментації можна визначити і масу кожної фракції. З рис. 14 видно, що відрізок Q₁ на осі ординат відповідає масі фракції великих часток, а відрізок Q₂ – масі фракції малих за розміром часток.

Поширивши ці міркування на полідисперсні системи, що складаються з великого числа фракцій, кожна з яких містить частинки однакового розміру, можна дійти висновку, що для таких систем графік седиментації зображується ламаною лінію з певним числом точок перегину. Дійсно, зазвичай експериментальна седиментаційна крива не є плавною кривою, а являє собою ламану лінію, що складається з прямолінійних ділянок (рис. 15, лінія OABCDEF). Як правило, на цій лінії можна виділити 5 – 6 відрізків, наявність яких свідчить про те, що дисперсна фаза складається з кількох фракцій.

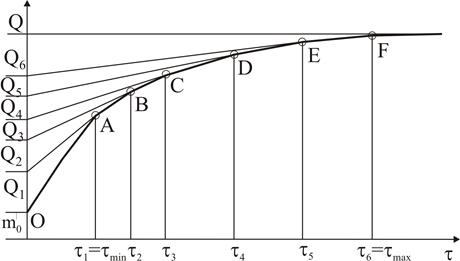
Рис. 15. Крива седиментації полідисперсної суспензії

Шляхом екстраполяції кожного з лінійних відрізків на вісь ординат можна розділити загальну масу частинок, що осідають, на фракції. Маси фракцій визначаються довжиною відрізків, які відтинаються на осі ординат Q подовженнями лінійних фрагментів ламаної OABCDEF (відрізки ОА,АВ, ВСі подалі відповідають масам фракцій Q₁, Q₂, Q₃ і т. д. ). Якщо прийняти величину відрізка OF (Q) за 100%, то за величинами відрізків Q₁, Q₂, Q₃ і т. д можна розрахувати масовий відсоток кожної фракції у суспензії:

.

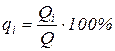(4.4)

Очевидно, що q₁ + q₂ + ... + q_n= 100 %.

Час осідання фракції з частинками певного розміру визначається координатою відповідної точки зламу кривої OABCDEF на осі абсцис (для т. А – τ₁, для т. В – τ₂ тощо).

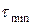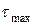За значеннями та розраховують мінімальні та максимальні значення радіусів частинок даної суспензії.

За результатами математичної обробки седиментаційної кривої будують диференціальну криву розподілу часток за розмірами 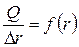(рис. 16). Оскільки частинки певної фракції мають фіксований радіус, то величину 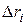розраховують за формулою 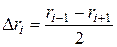для всіх радіусів, крім найбільшого 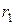= r_max та найменшого r_n = r_mіn. Для фракцій найкрупніших та найдрібніших частинок величини 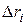обчислюють за формулами 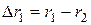та .

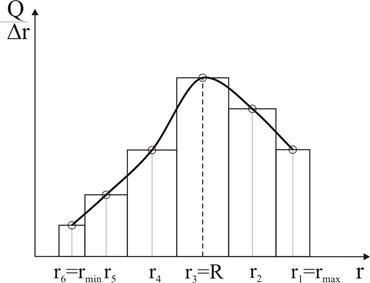
Рис. 16. Диференціальна крива розподілу часток за розмірами

Наведена на рис. 16 крива показує поширеність частинок у дисперсній системі залежно від їхнього розміру.Максимум на цій кривій відповідає фракції з частинками радіусу 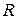, яку називають переважною, тому що масовий вміст цієї фракції у системі найбільшій. Радіус 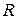найпоширеніших часток також називають переважним.

Читайте також:

1. II.ТЕОРЕТИЧНІ ПИТАННЯ КУРСОВОЇ РОБОТИ
2. IX. Відомості про військовий облік
3. IX. Відомості про військовий облік
4. Q Конституція України від 28 червня 1996 р. // Відомості Верховної Ради України – 1996 - № 30 – Ст. 141
5. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
6. Активне управління інвестиційним портфелем - теоретичні основи.
7. Білковий обмін: загальні відомості
8. Біографічні відомості
9. Боротьба з проявами національної самосвідомості
10. Вальниці ковзання. Загальні відомості
11. Види правосвідомості
12. Виникнення і розвиток свідомості у людини.

Переглядів: 1408