• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Теоретичні відомості

У механіці найпростішим осцилятором з одним ступенем вільності є пружинний маятник – тягарець масою m, що підвішений до невагомої абсолютно пружної пружини довжиною l, коефіцієнт жорсткості якої k.

На рис.1 показано тягарець масою m, підвішений до пружини довжиною l, який перебуває у стані спокою. У цьому положенні на тягарець діють сили тяжіння ( 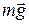) та пружності ( 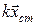). При цьому, згідно з законом Гука, маємо:

.

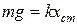де k – коефіцієнт жорсткості пружини;

x_ст – статична деформація пружини.

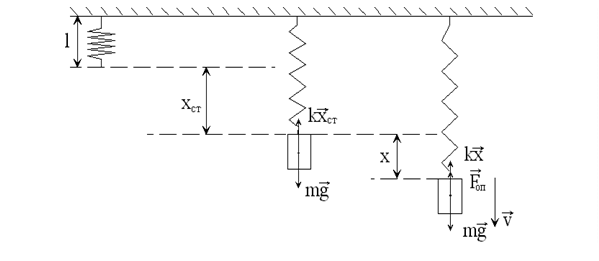
Рис. 1.

Охарактеризуємо зміщення тягарця з положення рівноваги координатою x, причому вісь x спрямуємо вздовж вертикалі вниз, а нуль осі з’єднаємо з положенням рівноваги тягарця.

Якщо вивести тягарець з положення рівноваги, розтягнувши пружину на величину x вниз (рис. 1) зовнішньою силою, то тягарець почне коливатися. За другим законом Ньютона маємо:

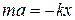. (1)

Оскільки прискорення дорівнює: ,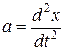

то:

.

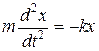Введемо позначення: 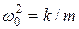, і отримаємо диференціальне рівняння гармонічних механічних коливань пружинного маятника:

,

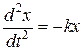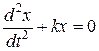. (2)

Розв’язок такого диференціального рівняння:

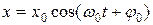, (3)

де x – зміщення тягарця масою m з положення рівноваги;

x₀ – амплітуда коливань пружинного маятника;

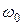– циклічна частота власних гармонічних механічних коливань пружинного маятника;

j₀ – початкова фаза коливань.

У реальних умовах під час коливань необхідно враховувати силу опору середовища. Для малих швидкостей руху 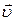сила опору середовища 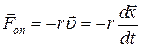, де r – коефіцієнт опору. Тоді диференціальне рівняння (2) набуває вигляду:

,

або:

.

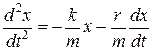Введемо позначення: 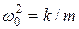, , 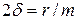і отримаємо диференціальне рівняння загасаючих механічних коливань пружинного маятника:

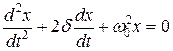. (4)

Розв’язок такого диференціального рівняння:

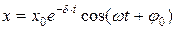, (5)

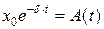– амплітуда загасаючих коливань пружинного маятника у момент часу t;

d – коефіцієнт загасання;

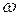– циклічна частота загасаючих механічних коливань пружинного маятника.

На рис. 2 показано графік залежності 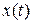при загасаючих механічних коливаннях пружинного маятника.

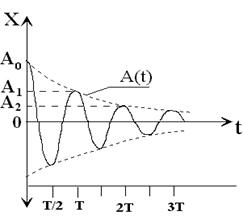
Рис. 2.

Маса тягарця m, коефіцієнт опору r і коефіцієнт жорсткості пружини k називаються параметрами осцилятора (коливальної системи), що розглядається, а величини x₀ і j₀ є константами, які визначаються з початкових умов.

Циклічна частота власних гармонічних механічних коливань пружинного маятника визначається за формулою:

.

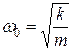Тоді період власних гармонічних механічних коливань пружинного маятника дорівнює:

.

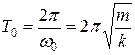Циклічна частота загасаючих механічних коливань пружинного маятника визначається співвідношенням:

.

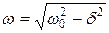Внаслідок загасання такі коливання не є строго періодичними. Тому під їх періодом розуміють інтервал часу між двома послідовними максимальними відхиленнями від положення рівноваги в один бік. Період згасаючих механічних коливань пружинного маятника дорівнює:

.

Логарифмічний декремент загасання q характеризує загасання (зменшення амплітуди коливань) за один період і визначається як натуральний логарифм відношення двох амплітуд, які відрізняються на один період T_З:

.

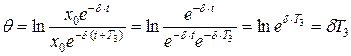Для N коливань: .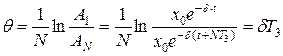

Часом релаксації t називається проміжок часу, протягом якого амплітуда коливань зменшується в e разів.

Оскільки: 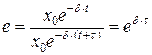, то: , .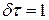

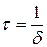Отже, час релаксації t обернено пропорційний коефіцієнту загасання коливань .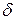

Якщо ввести N_e – число коливань, за яке амплітуда осцилятора зменшується в e разів, то 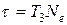і логарифмічний декремент загасання:

.

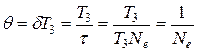Добротність коливальної системи 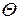характеризує відносну втрату енергії за одне коливання:

.

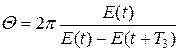Якщ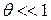о , то .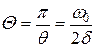

Таким чином, чим більша добротність системи, тим повільніше загасають коливання.

Читайте також:

1. II.ТЕОРЕТИЧНІ ПИТАННЯ КУРСОВОЇ РОБОТИ
2. IX. Відомості про військовий облік
3. IX. Відомості про військовий облік
4. Q Конституція України від 28 червня 1996 р. // Відомості Верховної Ради України – 1996 - № 30 – Ст. 141
5. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
6. Активне управління інвестиційним портфелем - теоретичні основи.
7. Білковий обмін: загальні відомості
8. Біографічні відомості
9. Боротьба з проявами національної самосвідомості
10. Вальниці ковзання. Загальні відомості
11. Види правосвідомості
12. Виникнення і розвиток свідомості у людини.

Переглядів: 487