• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Вибір оптимального маршруту

Враховуючи те, що круїз е круговим, в якості методу оптимізації обираємо методи рішення «задачі комівояжера».

Постановка завдання задачі комівояжера полягає в наступному: мається n портів, відстані між ними (табл. 1.3) задані у вигляді матриці C = (cij), де i.j = (1…n). В таблиці 1.3 кожному порту призначено номер від одиниці до n.

Кожне значення cij є відстанями між вихідним портом i та портом заходу j, тому їх величини не можуть мати від’ємного значення, тому cij 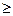0, .

В загальному випадку cij cji ( на приклад коли cji є вартість проїзду з міста j в місто i, яке не дорівнює переїзду з міста i в місто j ). Така задача вважається несиметричною. Враховуючи особливості роботи морського транспорту та географічне розташування портів круїзу, наша задача має симетричний характер, тобто cij = cji.

Треба знайти найкоротший замкнутий маршрут, який проходить через кожен порт тільки один раз з поверненням в перший базовий порт і який мінімізує сумарну пройдену відстань.

Математична постанова завдання може бути представлена в наступному вигляді:

;

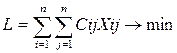(1.24)

(1.25)

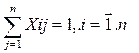
(1.26)

Xij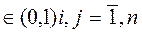

(1.27)

У РГЗ цю задачу варто вирішувати за допомогою засобу «Пошук рішення» програми електронних таблиць Microsoft EXCEL.

Інструкція для роботи із засобом «Пошук рішення» програми електронних таблиць Microsoft EXCEL наведена в додатку

Результати рішення задачі представляються у вигляді схеми.

У додатку А РГЗ необхідно представити відповідний «Звіт про результати» рішення задачі комівояжера.

Читайте також:

1. IV Етап: Вибір стратегії керування виявленими ризиками й виділення пріоритетних напрямків роботи
2. IV розділ. Сегментація ринку та вибір цільового сегменту
3. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
4. XV. Реалізація права вступників на вибір місця навчання
5. Абстрактна модель оптимального планування виробництва
6. Алгоритм адресного вибору оптимального безрецептурного вітаміновмісного лікарського препарату, лікарської форми і шляху введення
7. Алгоритм відшукання оптимального плану.
8. Алгоритм знаходження оптимального плану
9. Алгоритм планування податкових платежів. Вибір оптимального варіанту оподаткування та сплати податків.
10. АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОПТИМАЛЬНОГО РЕШЕНИЯ ОДНОИНДЕКСНЫХ ЗАДАЧ ЛП
11. Аудиторська вибірка
12. Багато вибіркові

Переглядів: 607