• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Способи розв’язування текстових задач

Щоб розв’язати задачу, необхідно виконати вимогу задачі (дати відповідь на питання задачі) через логічно правильну послідовність дій та операцій над числами, величинами і залежностями, що задані в умові задачі

Способами розв’язування задач є:

· арифметичний;

· алгебраїчний;

· графічний;

· практичний.

При арифметичному способі відповідь на питання задачі знаходять в результаті виконання арифметичних дій над числами. Різні арифметичні способи розв’язання однієї і тієї ж задачі відрізняються відношеннями між відомими в задачі, відношеннями між відомими і шуканими величинами, послідовністю використання цих відношень при виборі виконання арифметичних дій.

Приклад. З одного куща смородини зібрали 18 кг ягід, а з другого – 12 кг. Усі ягоди розклали в ящики, по 6 кг у кожний. Скільки ящиків використали?

1 спосіб.

1) 18 + 12 = 30 (кг) – всього ягід;

2) 30 : 6 = 5 (ящ.)

2 спосіб.

1) 18 : 6 = 3 (ящ.) – для ягід з першого куща;

2) 12 : 6 = 2 (ящ.) – для ягід з другого куща;

3) 3 + 2 = 5 (ящ.)

При алгебраїчному способі відповідь на питання задачі знаходять в результаті складання та розв’язування рівняння.

Приклад. Катер пройшов відстань між пристанями за течією річки за 2 год, а назад – за 3 год. Знайдіть власну швидкість катера, якщо швидкість течії річки 2км / год.

Розв’язання. Нехай власна швидкість катера х км / год. Тоді

(х + 2) км / год – його швидкість за течією,

(х – 2) км / год – швидкість катера проти течії,

(х + 2) · 2 км – катер пройшов за течією,

(х – 2) · 3 км – катер пройшов проти течії.

Так як відстані (х – 2) · 3км та (х + 2) · 2км рівні, то маємо наступне рівняння: (х – 2) · 3 = (х + 2) · 2

3х – 6 = 2х + 4

х = 10

Отже, власна швидкість човна – 10км / год.

Для розв’язання наступної задачі розглянемо використання графічного і практичного способів.

Задача. У гаражі стояло 9 машин, із них 2 мікроавтобуси, 3 легкові, а решта – вантажні. Скільки вантажівок стояло у гаражі?

Графічний спосіб. Цей спосіб дає можливість відповісти на питання задачі, не виконуючи арифметичних дій. Для цього накреслимо відрізок довжиною 9 клітинок, так як загальна кількість машин – 9. Позначимо м – мікроавтобуси, л – легкові машини, в – вантажівки. Тоді

Отже, 4 вантажівки стояло у гаражі.

Практичний спосіб. Позначимо кожну машину квадратом. Тому намалюємо 9 квадратів, залишивши ті ж самі позначення: м, л та в.

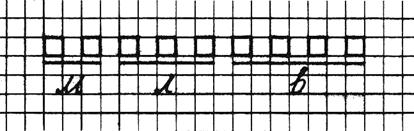
Для відповіді на запитання також не треба виконувати арифметичні дій, бо кількість вантажівок можна одержати, порахувавши відповідні квадрати (їх 4).

Читайте також:

1. I. Застосування похідної та інтеграла до роз’язування задач елементарної математики.
2. II.3. Основні способи і прийоми досягнення адекватності
3. А) Задачі, що розкривають зміст дій
4. АВТОМАТИЗАЦІЯ РОЗВ’ЯЗУВАННЯ КОМПЛЕКСУ ЗАДАЧ З ОБЛІКУ ОСНОВНИХ ЗАСОБІВ ТА НЕМАТЕРІАЛЬНИХ АКТИВІВ
5. Алгоритм розв’язання задачі
6. Алгоритм розв’язання задачі
7. Алгоритм розв’язання розподільної задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі
10. Алгоритм розв’язування задачі
11. Алгоритм розв’язування задачі
12. Алгоритм розв’язування задачі

Переглядів: 5322