• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Позиційні і непозиційні системи числення

Ідея нескінченності натурального ряду чисел освоювалось дуже повільно через відсутність протягом тривалого історичного періоду зручної системи числення. Перші системи числення були дуже недосконалими: для зображення кожного числа використовували окремий знак – ієрогліф. Пізніше ієрогліфи стали використовувати лише для позначення так званих вузлових чисел, решту чисел зображали за допомогою їх за принципом додавання або віднімання.

Зміст стародавньої єгипетськоїієрогліфічної системи можна побачити у таблиці

‌‌‌I

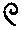
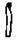
Стародавні єгиптяни лічили десятками. Але спеціальні знаки у них були лише для розрядів: одиниць, десятків, сотень і т. д. Числа від 1 до 10 записувались за допомогою паличок.

Наприклад, число 122 мало вид ς ∩∩I I .

У римський системі числення записували вузлові числа так: 1 - I, 5 – V, 10 – Х, 50 – L, 100 – C, 500 – D, 1000 – M. Решту чисел записували за принципом додавання або віднімання.

Наприклад, 256 – CCLVI, 399 – CCCXCIX.

Частково використовували і принцип множення: число 5 зображували символом руки, а 10 –як дві п’ятірки, тільки одна перевернута. Число 100 зображували буквою С, або (centum – сто), а 50 –L, як половину 100 (нижню половину).

Римською нумерацією користуємося і тепер. Ця система є непозиційною.

Непозиційними були також алфавітні системи: давньогрецька і старослов’янська. В цих системах перші 9 букв означали одиниці, наступні 9 – десятки, ще наступні – сотні.

У слов’янській нумерації було два способи лічби великих чисел: «мале словенське числення» і «велике словенське числення». У малому численні: 10⁴ – тьма, 10⁵ – легіон, 10⁶ – леодр. У великому: тьма (@) – 10⁶, легіон – 10¹² – тьма тем, леодр – легіон легіонів – 10²⁴, леодр леодрів – 10⁴⁸ – ворон.

Перша позиційна система числення виникла понад 2000 років до н.е. в стародавньому Вавилоні. Це була шістдесяткова позиційна нумерація. Проте принцип позиційного значення цифр тут ще не використовувався скрізь. Для запису чисел використовували положення клину : ▼- 1 і 60, ◄ - 10. Інші числа зображувались за допомогою цих знаків і дій додавання.

Сучасна позиційна система числення була винайдена в Індії у V-VI ст. Через арабів вона поширилася в IX ст. в Середню Азію, а пізніше – і в Західну Європу. Великим досягненням індійської математики було введення нуля для позначення відсутності одиниць розряду в числі. Після цього десяткова система числення стала повністю оформленою. Запровадження десяткової системи числення на Русі було зупинено монгольським ігом. Тільки у XVIII ст. індійська система числення витіснила слов’янську нумерацію.

У сучасному житті використовують також інші системи числення. В астрономії з давніх-давен застосовується шістдесяткова система числення. Основою цієї системи є число 60. Так, 60сек = 1 мінута, або 60^// = 1^/, 60^/ = 1^° тощо.

Взагалі, основою числення може бути будь-яке натуральне число р ≥2. Для запису числа в такій системі числення використовується р символів: 0,1, ..., р-1.

Означення:Записом цілого невід’ємного числа х у р-й системі числення називається його подання у вигляді х = а_npⁿ + … + a₁p + a₀, де a_n, …, a_1, a₀ набувають значення 0, 1, ..., р-1, а_n ≠ 0 .

Числа 1, p, p², … , pⁿ називають розрядними одиницями 1-го, 2-го, ... , (n+1)-го розрядів.

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. POS-системи
8. T. Сутність, етіологія та патогенез порушень опорно-рухової системи
9. VI. Філогенез нервової системи
10. А) Заробітна плата її форми та системи.
11. А) Заробітна плата, її форми та системи.
12. А) Поліпшення системи зворотного зв'язку.

Переглядів: 1652