• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Від’ємні числа. Множина дійсних чисел

Натуральні числа виникли на початку розвитку людства у зв’язку з лічбою предметів. Потреба вимірювання величин, а також вимога виконання обернених операцій, зокрема ділення, добування кореня і логарифмування, привели до введення дробових та ірраціональних чисел.

Як і коли виникли від’ємні числа?

Поняття про від’ємні числа виникло значно пізніше, ніж поняття дробових і ірраціональних чисел. Введення від’ємних чисел було новим етапом розширення поняття числа, викликаним практичною необхідністю; по-перше, потребою вимірювання напрямлених величин і величин, які можна розуміти в двох протилежних значеннях (температура – тепло і холод; час – майбутній і минулий; економія матеріалів і перевитрата і т.ін.); по-друге, потребою в розв’язуванні практичних задач, що приводять до віднімання від меншого числа більшого. Обидві ці задачі тісно пов’язані між собою.

Вперше від’ємні числа почали використовувати в Китаї в І ст. до н.е. у зв’язку з розв’язуванням рівнянь. Оскільки в ті часи знаків «плюс» і «мінус» ще не було, то на відміну від додатних чисел китайці зображали від’ємні числа іншим кольором. Додатними числами позначали майно, наявні гроші, прибуток. Їм раділи і зображали їх червоним кольором (китайці їх називали «чен»). Від’ємними числами позначали борг, збиток і зображали їх чорним кольором («фу»).

Індійські математики Брахмагупта (VII ст.) і Бхаскара (XII ст.) дали такі правила дій над від’ємними і додатними числами: «Сума майна і майна є майно». «Сума двох боргів є борг». «Сума майна і боргу дорівнює різниці». «Сума майна і рівного йому боргу дорівнює нулю». «Добуток боргу на борг є майно» і т.ін.

Проте важко було уявити, як це з «боргів» (перемноження за схемою 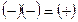) може вийти «майно»? Тому довго від’ємні числа не визнавали справжніми, вважали їх недійсними, абсурдними, фіктивними. Бхаскара писав, що люди не схвалюють від’ємних чисел.

У Європі вперше від’ємні числа почав використовувати італійський математик Л.Фібоначчі (XII – XIII ст.). Німецький математик М.Штіфель (XVI ст.) назвав їх «числами, меншими ніж ніщо» (меншими від нуля). Людям важко було миритися з тим, що існує величина, «менша ніж ніщо». Сам Штіфель писав, що нуль знаходиться між істинними і абсурдними числами. Тільки після того, як у XVІI ст. французький математик Рене Декарт у відомій книзі «Геометрія» зобразив на числовій прямій додатні числа праворуч від нуля, від’ємні числа – ліворуч, їх почали визнавати дійсними числами.

Від’ємне число можна розглядати як різницю між меншим дійсним числом і більшим, якщо ця різниця виражає значення величини, протилежне значенню, що виражається дійсним числом (тепло і холод, борг і наявні гроші, прибуток і збиток, вправо і вліво тощо).

Від’ємні числа слід розглядати в тісному взаємозв’язку з додатними числами, причому не тільки в протиставленні їх додатним числам, а й в діалектичній єдності з ними.

Нова розширена множина містить у собі відомі вже невід’ємні числа як свою підмножину. Множина від’ємних чисел не містить у собі множини чисел додатних, як це було з множиною дробів, яка містила в собі числа натуральні. Навпаки, тут кожному додатному дійсному числу ставиться у відповідність протилежне йому від’ємне число. При цьому число нуль набуває нового смислу як число, яке «розділяє» додатні і від’ємні числа і належить ні до тих, на до інших. Разом же всі додатні, від’ємні числа і нуль об’єднуються в одну множину – множину дійсних чисел R. Саме в цьому і виявляється діалектична єдність додатних і від’ємних чисел.

Звертаємо увагу на недопустимість ототожнення смислу виразів виду «нуль карбованців» і «нуль градусів». Вираз «температура 0°» зовсім не означає відсутність температури (хоч іноді у повсякденному житті при вимірюванні температури людського тіла і говорять «немає температури» замість «температура нормальна»),

Невід’ємні числа – це числа нової природи, вони мають свої особливості і тому на них не можуть бути механічно перенесені всі властивості додатних чисел, зокрема означення і закони дій.

Поняття «правильний дріб» має смисл лише для додатних дробів.

Особливість частки від ділення двох раціональних чисел, із яких хоча б одне від’ємне, пов’язана з неможливістю кратного порівняння цих чисел, яка зумовлюється тим, що напрямлені величини (вектори) можна порівнювати в кратному відношенні лише за модулем (довжиною).

Оскільки від’ємні числа є числами нової природи, введення їх потребує перегляду існуючих означень прямих дій, розширення їх у випадку, коли для нових чисел вони не мають попереднього смислу.

Кожному додатному числу на числовій прямій відповідає так саме за величиною число, але із знаком мінус. Такі пари дійсних чисел називаються протилежними числами.

Наприклад, +1 і –1; +2,5 і –2,5; +3,(8) і –3,(8), 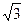і – 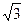і т.ін.

Тільки нуль без пари: він не належить ні до додатних, ні до від’ємних чисел: –0= +0 = 0. Як відомо знак «+» перед додатними числами, як правило, не ставиться.

Із двох від’ємних чисел те більше, модуль якого менший.

Означення. Сумою двох дійсних чисел одного знака називається сума їх модулів, взята з тим самим знаком, який мають доданки.

Сумою двох дійсних чисел, взятих з різними знаками, називається різниця між більшим і меншим модулем даних чисел, взята із знаком числа, модуль якого більший.

Наслідки.

1. Сума двох протилежних дійсних чисел дорівнює нулю: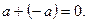

2. Сума двох дійсних чисел, одне з яких дорівнює нулю, дорівнює другому доданку: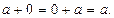

Введене означення суми дійсних чисел узагальнюється на випадок будь-якої кількості доданків.

Безпосередньо із означення дійсного числа та з означення суми дійсних чисел випливають основні властивості дії додавання дійсних чисел, які мали місце на множині дійсних невід’ємних чисел.

Означення дії віднімання дійсних чисел залишається таким самим, як і для дійсних невід’ємних чисел.

Означення. Відняти від дійсного числа а дійсне число b – це означає знайти таке дійсне число х, яке в сумі з b дає а: ,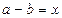

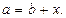
Правило. Щоб знайти різницю двох дійсних чисел, треба до зменшуваного додати число, протилежне від’ємнику: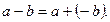

Оскільки віднімання дійсних чисел зводиться до додавання, то у множині дійсних чисел додавання і віднімання об’єднують в одну дію, яку називають алгебраїчним додаванням.

Означення. Вираз, що являє собою запис кількох дійсних чисел, послідовно з’єднаних знаками дій додавання і віднімання, називається алгебраїчною сумою дійсних чисел.

Означення. Добутком двох дійсних чисел називається добуток їх модулів, якщо дані числа з однаковими знаками або хоч одне з них нуль, і число, протилежне добутку їх модулів, якщо числа з різними знаками.

Правило. Щоб перемножити кілька дійсних, відмінних від нуля чисел, треба перемножити їх модулі і взяти результат із знаком «плюс», якщо число від’ємних співмножників парне, і із знаком «мінус», якщо число від’ємних співмножників непарне.

Основні закони дії множення зберігаються і на множині всіх дійсних чисел.

Означення.Знайти частку від ділення дійсного числа а на b, це означає знайти таке дійсне число с, щоб задовольнялася умова , де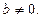

Правило. Частка від ділення двох дійсних чисел дорівнює частці від ділення модуля діленого на модуль дільника із знаком «плюс», якщо ділене і дільник є числа з однаковими знаками, із знаком «мінус», якщо ділене і дільник числа з різними знаками.

Підкреслюємо, що і у множині дійсних чисел ділення на нуль виключається, оскільки у випадку 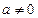немає такого дійсного числа с, щоб виконувалася умова ; у випадку будь-яке дійсне число с задовольняє умову .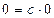

Частка дорівнює нулю тоді і тільки тоді, коли ділене дорівнює нулю. Звідси випливає, що рівняння виду 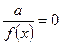при 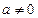не має розв’язку.

Частка 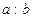, де , завжди існує, і притому єдина. Окремі випадки ділення: , якщо ; ; .

Таким чином, у множині дійсних чисел виконуються всі чотири арифметичні дії (за винятком ділення на нуль).

Питання для самоконтролю

1. У чому полягає необхідність розширення множини цілих невід’ємних чисел?

2. Дати означення дробу; рівних дробів.

3. Сформулювати і довести необхідну і достатню умови рівності двох дробів.

4. Що називають множиною додатних раціональних чисел?

5. Який дріб називається правильним; неправильним?

6. Сформулювати основну властивість дробу.

7. У чому полягає застосування основної властивості дробу?

8. Розкрити вивчення поняття дробу в початковій школі.

9. Яке число називається мішаним?

10. Які числа називаються взаємно оберненими?

11. Сформулювати означення суми, різниці, добутку, частки додатних раціональних чисел?

12. Сформулювати закони додавання і множення невід’ємних раціональних чисел.

13. В чому полягає упорядкованість множини додатних раціональних чисел?

14. Який дріб називається десятковим?

15. В чому полягає основна властивість десяткового дробу?

16. Як подати звичайний дріб у вигляді десяткового?

17. Який дріб називається нескінченним десятковим періодичним дробом?

18. Який дріб називається чистим періодичним десятковим дробом?

19. Який дріб називається мішаним періодичним десятковим дробом?

20. Якому звичайному дробові дорівнює чистий періодичний десятковий дріб?

21. Якому звичайному дробові дорівнює мішаний періодичний десятковий дріб?

22. Що таке процент (відсоток)?

23. Розкрити поняття про ірраціональні числа.

24. Розкрити поняття про від’ємні числа.

25. Як утворилась множина дійсних чисел?

26. Що називається модулем дійсного числа?

27. Сформулювати правила додавання, віднімання, множення, ділення дійсних чисел.

Читайте також:

1. II. Множення круглих багатоцифрових чисел на розрядні числа.
2. N – чисельність популяції
3. Аксіома неперервності дійсних чисел
4. Алгоритм додавання цілих невід’ємних чисел
5. Алгоритми переведення чисел з однієї позиційної системи числення в іншу
6. Аналіз чисельності, складу і руху персоналу
7. Введення чисел.
8. Верхня і нижня грані дійсних чисел
9. Види недійсних правочинів та їх правові наслідки
10. Визначення добутку двох цілих невід’ємних чисел як числа елементів декартового добутку двох скінченних множин
11. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
12. Визначення добутку цілих невід’ємних чисел через суму. Операція множення цілих невід’ємних чисел

Переглядів: 3345