• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Початкові відомості

З метою дослідження топології та перетворення структури транспортної мережі доцільно використовувати апарат теорії графів, як засіб її формалізації.

За допомогою теорії графів, як розділу математики, вивчаються та досліджуються закономірності графічних об’єктів (звідки випливає й назва). Теорія графів як наука сформувалась в середині 30 – х років 20 століття.

Геометрично граф – це сукупність точок та з’єднуючих їх ліній.

Математично граф існує, якщо задано непусті множини , при цьому кожному елементу множини U поставлена у відповідність впорядкована пара елементів (i, j) з множини І. Елементи множини І називаються вершинами графа, а елементи множини U – ребрами графа. Як приклад маємо граф (рис.8.1).

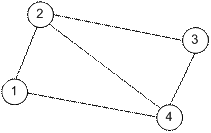
Рис. 8.1. Приклад математичного графа

Найбільше розповсюдження при формалізації топології об’єктів теорія графів набула в таких галузях науки як електротехніка (електричні схеми), хімія (структура зв’язків між атомами та молекулами органічних сполук), транспортні системи (схеми залізничних станцій, транспортних вузлів тощо). Це також можуть бути зв’язки та відношення між людьми, подіями та станами якихось об’єктів.

Теорія графів пов’язана з таким математичним апаратом як: теорія множин, теорія ймовірностей, теорія матриць, математична логіка.

Перше застосування теорії графів пов’язане із розв’язанням відомим математиком Леонардом Ейлером у 1736 році задачі про Кенігсбергські мости (рис. 8.2, а), яка формулювалась таким чином: чи можна, вийшовши з будь-якої частини міста та пройшовши всіма 7 мостами, повернутись на початкове місце, ідучи тільки один раз по кожному містку. Цю задачу можна розглядати як приклад оптимізації маршруту для екскурсійного бюро.

Рис. 8.2 План міста Кенігсберг (а) та відповідний йому граф (б).

Представивши план міста у вигляді графа (рис. 8.2, б), Л. Ейлер довів, що поставлена задача не має вирішення. Воно може існувати у тому випадку, коли кожна вершина зв’язана з парним числом ребер.

Читайте також:

1. IX. Відомості про військовий облік
2. IX. Відомості про військовий облік
3. Q Конституція України від 28 червня 1996 р. // Відомості Верховної Ради України – 1996 - № 30 – Ст. 141
4. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
5. Білковий обмін: загальні відомості
6. Біографічні відомості
7. Боротьба з проявами національної самосвідомості
8. Вальниці ковзання. Загальні відомості
9. Види правосвідомості
10. Види та жанри образотворчого мистецтва, методика ознайомлення з ними у початковій школі.
11. Виникнення і розвиток свідомості у людини.
12. Виникнення людської свідомості. Мова і свідомість.

Переглядів: 595