Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ЕЛЕМЕНТА ТІЛА. ТЕОРІЇ МІЦНОСТІ

Під напруженим станом (НС) в точці тіла розуміють сукупність напружень, що діють на різних площадках, проведених через цю точку. Якщо в усіх точках тіла НС однаковий, то він називається однорідним (наприклад, при осьовому розтяганні–стисканні), якщо ж він не однаковий, то – неоднорідним НС. У загальному випадку в довільній точці НС тіла неоднорідний і для його дослідження в околі цієї точки виділяють елементарний паралелепіпед, в якому кожні три примикаючі одна до одної площадки (грані) взаємно перпендикулярні. Внаслідок малості виділеного елемента можна вважати, що напруження на кожній його площадці розподілені рівномірно й НС елемента однорідний. У загальному випадку на гранях елемента діють нормальні (σ) та дотичні напруження (τ). Але завжди є така орієнтація елемента в тілі, коли на його гранях (площадках) будуть відсутні дотичні напруження ( ). Такі площадки називають головними, а діючі по них нормальні напруження – головними напруженнями. Напрями, паралельні головним напруженням, називають головними напрямами. При об’ємному НС всі три головні напруження відрізняються від нуля й позначаються , та 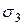, причому 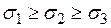, в алгебраїчному розумінні.

При плоскому НС одне з головних напружень дорівнює нулю або на двох паралельних площадках елемента відсутні любі напруження. Зображуючи елемент, який перебуває в плоскому НС, суміщатимемо відповідну (нульову) головну площадку з площиною креслення (рис. 2.1).

Вважаємо нормальні напруження додатними при розтяганні ( 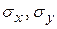на рис. 2.1), а дотичні – додатними, якщо вони намагаються обертати розглядуваний елемент за ходом годинникової стрілки ( 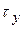на рис. 2.1). З урахуванням закону парності дотичних напружень ( ) плоский НС у загальному випадку може характеризуватися трьома неголовними напруженнями 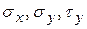, що діють на довільно орієнтованих взаємно перпендикулярних площадках, або двома головними напруженнями .

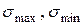Рис. 2.1

Якщо задані неголовні площадки, на яких діють відомі напруження 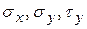, то напруження, що діють на довільних похилих (косих) площадках, розмішених під кутами 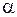та до початкової площадки, визначаються за такими формулами:

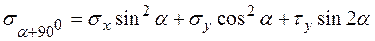, (2.1)

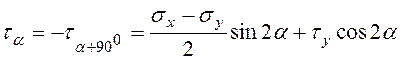Додатні кути та відраховуються від додатного напряму осі х проти ходу годинникової стрілки.

При плоскому НС головні напруження визначаються за формулою

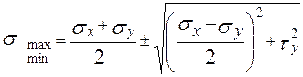. (2.2)

Тут знак „+” відповідає 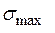, а знак „–” відповідає .

Напрям вказаних головних напружень і положення відповідних головних площадок визначаються кутами та 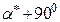, які знаходяться з рівняння

. (2.3)

Знаки для кутів та 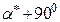такі ж, що й для кутів та .

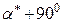З двох взаємно перпендикулярних головних напрямів, що визначені кутами та , напрям 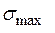проходить через ті чверті елемента, в яких стрілки дотичних напружень сходяться до спільного ребра.

Існує властивість інваріантності суми нормальних напружень на взаємно перпендикулярних площадках у точці. При об’ємному НС

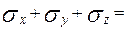
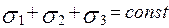а при плоскому НС

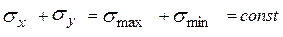. (2.4)

Екстремальні дотичні напруження при об’ємному НС

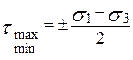а при плоскому НС

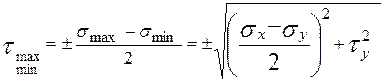. (2.5)

Площадки, по яких діють екстремальні дотичні напруження, паралельні напряму 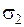і нахилені під кутом 45° до напрямів та .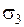

Умови міцності елемента тіла за п’ятьма найпоширенішими теоріями міцності такі:

за І теорією міцності (найбільших нормальних напружень)

, ; (2.6)

за П теорією міцності (найбільших лінійних деформацій)

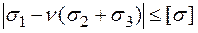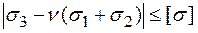, ; (2.7)

за Ш теорією міцності (найбільших дотичних напружень)

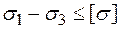; (2.8)

за ІV теорією міцності (енергетичною)

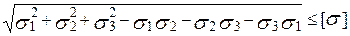; (2.9)

за теорією міцності Мора

, (2.10)

де і – допустимі нормальні напруження відповідно при розтяганні та стисканні.

Перша теорія міцності не відображує пластичні властивості матеріалу й забезпечує задовільні результати лише при деяких напружених станах для дуже крихких матеріалів (цегла, кераміка, інструментальна сталь).

Друга теорія міцності експериментально підтверджується лише для крихкого стану матеріалу (легійовані чавуни, високоміцні сталі після низького відпуску). Її недопустимо використовувати, якщо матеріал не підкоряється закону Гука або знаходиться за границею пропорційності.

Третя теорія міцності експериментально підтверджується для пластичних матеріалів, які однаково працюють на розтягання та стискання (для багатьох металів та їх сплавів). Недоліком теорії є те, що вона не враховує проміжне головне напруження .

Четверта теорія міцності експериментально підтверджується, як і третя, для пластичних матеріалів, які однаково працюють на розтягання та стискання (для багатьох металів та їх сплавів). Ця теорія краща за третю.

Теорія міцності Мора дозволяє враховувати різну спроможність матеріалів опиратися розтяганню та стисканню, зокрема крихких.

Лінійні деформації елемента за трьома головними напрямами (для об‘ємного НС) визначаються за формулами узагальненого закону Гука:

, (2.11)

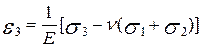Відносна об‘ємна деформація елемента тіла

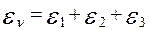, (2.12)

або з урахуванням виразів (2.11)

. (2.13)

Розглядаючи плоский НС, у виразах для об’ємного НС слід покласти відповідне головне напруження рівним нулю.

У випадку об’ємного НС, коли маємо справу з неголовними площадками, лінійні деформації елемента за напрямами x, y та z визначаються за наступними формулами узагальненого закону Гука:

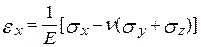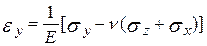, (2.14)

Відносна об‘ємна деформація елемента тіла

, (2.15)

або з урахуванням (2.14)

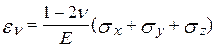. (2.16)

Розглядаючи плоский НС, у виразах (2.14-2.16) слід покласти відповідне нормальне напруження рівним нулю (у розглядуваному випадку ).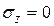

Приклад розв’язання задачі № 3.Для кубика (елемента тіла), на гранях якого діють напруження і 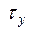, потрібно зробити наступне: а) визначити положення головних площадок і значення головних напружень; б) перевірити міцність кубика за найпоширенішими теоріями міцності; в) визначити відносні та абсолютні лінійні деформації у трьох головних напрямах; г) визначити відносне та абсолютне змінювання об’єму елемента; д) визначити та на площадках, що розташовані під кутами =30^o та +90^o=120^o відносно площадки, на якій діє . Вважати довжину ребер кубика по головних напрямах а=0,1 м; 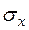=100 МПа, 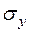=–60 МПа, 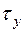=–50 МПа; 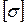=160 МПа; = 0,3 і МПа.

Кубик знаходиться в плоскому напруженому стані. Зображуємо плоский елемент з дійсними напрямами дії заданих напружень (рис. 2.2)

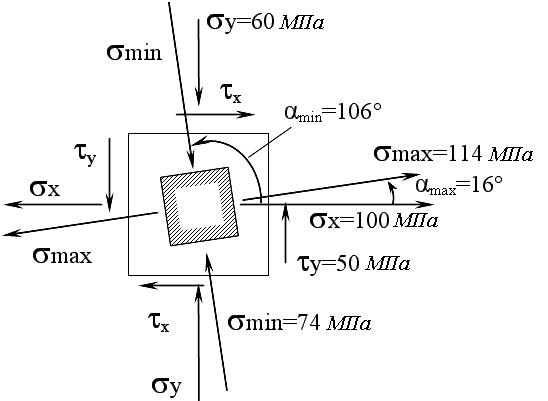
Рис. 2.2

Визначимо положення головних площадок і значення головних напружень.

Спочатку визначаємо кут :

;

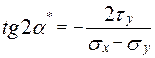
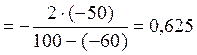тоді 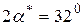, а .

Оскільки стрілки дотичних напружень сходяться до спільного ребра елемента у першій та третій чвертях елемента (рис. 2.2), то напрям визначається кутом 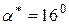, а напрям визначається кутом .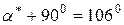

Далі визначаємо головні напруження

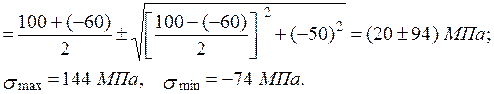
Ми бачимо, що екстремальність головних напружень відносно заданих 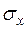та виконується.

Далі перевіримо виконання властивості інваріантності

;

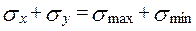100 + (– 60) = 114 + (– 74); 40 ≡ 40.

Для перевірки правильності визначення положення головних площадок скористаємось умовою, що на головних площадках :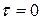

;

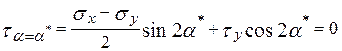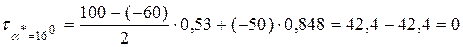Дійсні напрями напружень і положення головних площадок відносно неголовних площадок показані на рис. 2.2.

Перевіримо міцність елемента. Спочатку встановимо відповідність між головними напруженнями при плоскому та об’ємному НС ( ):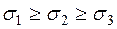

За І теорією міцності:

, ;

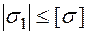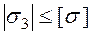Обидві умови міцності виконуються.

За ІІ теорією міцності при =0,3:

, ;

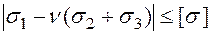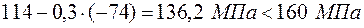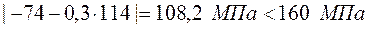Обидві умови міцності також виконуються.

За Ш теорією міцності:

;

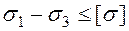Умова міцності не виконується.

За IV теорією міцності:

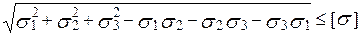Умова міцності теж не виконується.

В нас , тобто матеріал однаково працює на стискання та розтягання. Тому перевіряти умову міцності за теорією Мора немає ніякого сенсу.

Визначимо лінійні деформації елемента по головних напрямах. Використовуючи формули узагальненого закону Гука

, ,

;

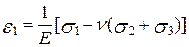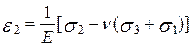отримуємо

;

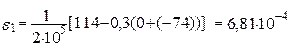Абсолютні деформації елемента по головних напрямах будуть такими:

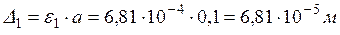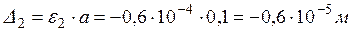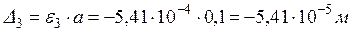Відносна об’ємна деформація елемента така

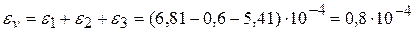Те ж саме повинні одержати, якщо скористаємось іншою формулою:

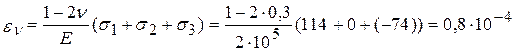Абсолютна зміна об’єму елемента така

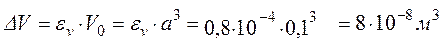де – об’єм елемента до деформації.

Напруження, що діють на похилих площадках, розміщених під кутами =30^o та +90^o=120^o відносно головної площадки з , визначаються за формулами, отриманими з (2.1), якщо покласти в них 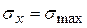, , 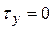та :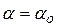

, ,

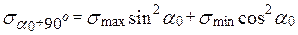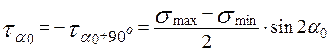Після підстановки числових значень матимемо:

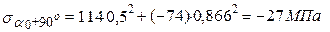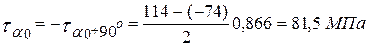Перевіримо правильності визначення та . Екстремальність головних напружень відносно визначених напружень та виконується. Далі перевіримо виконання властивості інваріантності:

67 + (– 27) = 114 + (– 74); 40 ≡ 40..

Дійсні напрями напружень та положення площадок показані на рис. 2.3.

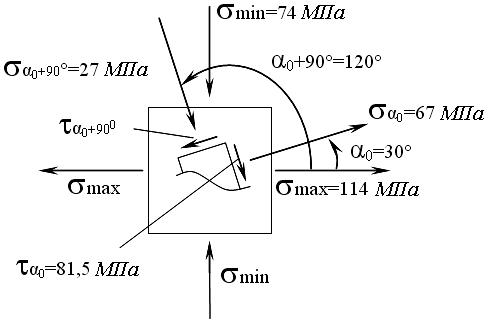
Рис. 2.3

Контрольні запитання

1. Що характеризує напружений стан тіла у точці?

2. Які існують види напружених станів?

3. Які площадки та напруження називають головними та скільки їх для кожного з напружених станів?

4. У чому зміст закону парності дотичних напружень та як записується закон парності дотичних напружень при плоскому напруженому стані?

5. На яких площадках діють екстремальні нормальні та дотичні напруження?

6. Як визначається положення головних площадок, значення та напрям дії головних напружень?

7. Яку властивість має сума нормальних напружень, що діють на взаємно перпендикулярних площадках?

8. Які значення мають екстремальні дотичні напруження при лінійному, плоскому та об'ємному напружених станах, а також на яких площадках вони діють?

9. Як відносно головних площадок зорієнтовані площадки, на яких діють екстремальні дотичні напруження?

10. Як визначаються напруження, що діють на похилих площадках, якщо задані площадки є неголовними?

11. Як визначаються напруження, що діють на похилих площадках, якщо задані площадки є головними?

12. Як записуються формули узагальненого закону Гука для плоского та об'ємного напружених станів?

13. Як формулюються умови рівноміцності для чотирьох класичних теорій міцності (І, ІІ, ІІІ і ІV-ої) та як записуються умови міцності для цих теорій?

14. Я записується умова міцності за теорією Мора?

15. Які теорії міцності слід використовувати для пластичних матеріалів?

16. Які теорії міцності слід використовувати для крихких матеріалів?

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
ЗАДАЧА № 3	\|	ЗАДАЧА № 4

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.017 сек.