
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Класифікація економіко-математичних моделей.
ОПТИМІЗАЦІЙНІ МЕТОДИ ТА МОДЕЛІ
Конспект лекцій
Сєвєродонецьк 2013р.
УДК
Конспект лекцій з дисципліни «Оптимізаційні методи та моделі»
для напряму підготовки: 6.030504 «Економіка підприємства»/ Укл. О.Л. Бродський – Сєвєродонецьк: Вид-во ТI - 2013. – 84 с.
Розроблено на підставі робочої програми дисципліни «Оптимізаційні методи та моделі»
| Укладач | ______________ | О.Л. Бродський, доцент |
| Відповідальний за випуск | ______________ | О.В. Поркуян, зав. каф. ВПМ, проф., д.т.н. |
| Рецензент | ______________ | Н.В. Швець, доцент каф. ЕП |
Вступ
Дисципліна «Оптимізаційні методи та моделі» є частиною більш об’ємного курсу «Економіко-математичне моделювання».
Метою навчання є наукове кількісне обґрунтування рішень, що приймаються по управлінню в господарчих, фінансових, державних та інших справах.
Інструментом, що застосовується для постановки та розв’язання відповідних задач є математичне моделювання, тобто створення математичних моделей виробничих, торгових, транспортних та інших процесів.
Оптимізаційні моделі охоплюють випадки безпосереднього економічного формулювання мети розв’язання проблеми.
Конспект містить 14 лекцій відповідно до діючого робочого плану спеціальності «Економіка підприємства».
Розглянуті лінійні та нелінійні моделі різних рівнів та методи розв’язання задач оптимізації в умовах цих моделей.
Зміст
1. Вступ………………………………………………………………………..3
2. Лекція 1.Концептуальні аспекти математичного моделювання економіки.Оптимізаційні економіко-математичні моделі…….5
3.Лекція 2.Задачі лінійного програмування та методи їх розв’язування...8
4.Лекція 3.Розв’язування задачі лінійного програмування не в канонічній формі.Двоїстість у лінійному програмуванні………………16
5.Лекція 4. Цілочисельне програмування………………………………...21
6.Лекція 5.Транспортна задача. Побудова опорного плану……………..28
7. Лекція 6. Транспортна задача. Поліпшення плану. Розв’язування задачі у відкритій моделі…………………………………………… 34
8. Лекція 7. Моделі галузевого планування………………………………42
9. Лекція 8. Моделі управління запасами…………………………………46
10.Лекція 9. Багатопродуктові моделі управління запасами…………….53
11. Лекція 10. Ймовірносні моделі управління запасами. Основні поняття теорії ігор……………………………………………………59
12. Лекція 11. Матричні ігри………………………………………………..63
13.Лекція 12. Зведення матричної гри до задачі лінійного програмування. …………………………………………….69
14. Лекція 13. Ігри з природою…………………………………………….73
15. Лекція 14. Динамічні моделі…………………………………………...77
Лекція 1
Концептуальні аспекти математичного моделювання економіки
Оптимізаційні економіко-математичні моделі
- Економіко-математичним моделювання
- Класифікація економіко-математичних моделей
- Задача оптимального планування випуску продукції
- Загальна задача лінійного програмування
1. Економіко-математичним моделювання
Моделлю називається спеціально створений об'єкт, на якому відтворюються визначені характеристики досліджуваного об'єкта з метою дослідження його форми, співвідношень, властивостей.
Метод, що включає в себе побудову моделі, називається моделюванням.
За способом побудови розрізняють моделі: логічні, фізичні, математичні.
Математичною моделлю називається опис об'єкта (процесу) рівняннями, нерівностями та іншими засобами математики.
Економіко-математичним моделюванням називається теорія, методи та алгоритми розв’язання задач з економічним змістом у математичній формі.
Потреба в такому моделюванні виникає в різних задачах економічного аналізу, планування, прогнозування та ін.
Математичні методи одержання розв’язків для найпростіших задач об’єднані назвою математичне програмування.
2.Класифікація економіко-математичних моделей
Схема економіко-математичного моделювання:
1) постановка задачі;
2) побудова формалізованої схеми;
3) побудова моделі;
4) дослідження моделі;
5) оцінка отриманого рішення задачі.
Класифікація економіко-математичних моделей.
1) За цільовим призначенням:
теоретичні;
прикладні.
2) За характером залежності від часу:
статичні (більш прості, тому що не враховують зміну в часі);
динамічні (враховують динаміку).
3) За характером відображення причинно-наслідкового зв'язку:
детерміновані;
ймовірнісні (стохастичні);
усереднені.
4) За математичною складністю:
лінійні;
нелінійні.
5) За характером вимог до результатів:
балансові (у чистому вигляді майже немає);
оптимізаційні.
6) За глибиною горизонту часу:
поточні (застосовуються для досить простих явищ);
перспективні;
довгострокового прогнозування.
7) За повнотою охоплення економічних процесів:
макромоделі;
мікромоделі.
3. Задача про оптимальний план випуску продукції
Деяке підприємство може випускати n видів виробів (товарний асортимент). Для випуску використовуються m видів ресурсів (сировина, енергія, праця). Відома матриця питомих витрат різних ресурсів для виробництва усіх видів продукції:  ,i=1,...,m - номер ресурсу; j=l,...n - номер виробу.
,i=1,...,m - номер ресурсу; j=l,...n - номер виробу.
Задано обсяги всіх наявних ресурсів bi; ціни сj (норми прибутку) за кожнім виробом.
Потрібно скласти оптимальну виробничу програму (план випуску), що забезпечує підприємству максимальний доход (максимальний прибуток). Уведемо вектор змінних xj: x1, x2, ...xn – обсяг (кількість) продукції відповідного виду.
Доход (прибуток) одержимо множенням ціни (норми прибутку) на обсяг продукції: сj xj
Загальний доход 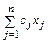 .
.
Загальні витрати за кожним видом ресурсів:
 ; i=1, ...m.
; i=1, ...m.
Одержимо наступну модель:

| (1.1) |
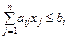 ; i=1,2,...,m ; i=1,2,...,m
| (1.2) |
 ; j= 1,2,... n ; j= 1,2,... n
| (1.3) |
Зміст нерівностей (1.2): загальні витрати ресурсів не можуть бути більше наявних обсягів цих ресурсів.
Зміст (1.3): вироби кожного виду або випускаються (xj > 0), або ні (xj=0); xj < 0 тут економічного змісту не має.
Математичний зміст задачі (1.1) - (1.3): задача на умовний екстремум функції багатьох змінних; ліва частина (1.1) називається цільовою функцією, нерівності (1.2) і (1.3) утворюють систему обмежень задачі.
Математична модель називається лінійною, якщо всінерівності і рівняння моделі є лінійними. Розділ курсу, у якому розглядаються лінійні моделі, називається лінійним програмуванням.
Читайте також:
- II. Класифікація видатків та кредитування бюджету.
- V. Класифікація і внесення поправок
- V. Класифікація рахунків
- А. Структурно-функціональна класифікація нирок залежно від ступеню злиття окремих нирочок у компактний орган.
- Адміністративні провадження: поняття, класифікація, стадії
- Аналіз розв’язків спряжених економіко-математичних задач
- Аналітичні процедури внутрішнього аудиту та їх класифікація.
- АТОМНО-МОЛЕКУЛЯРНЕ ВЧЕННЯ. КЛАСИФІКАЦІЯ НЕОРГАНІЧНИХ СПОЛУК
- Базова класифікація ризиків підприємств
- Баланс енергій у видобувній свердловині і класифікація видобувних свердловин за способом їх експлуатації
- Банківська платіжна картка як засіб розрахунків. Класифікація платіжних карток
- Банківський кредит та його класифікація.
Переглядів: 2207
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Загальна задача лінійного програмування (ЗЛТ) |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |