
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розв’язування задач на мінімум цільової функції
Розглянемо задачу:
Z = C ∙ X " min
AX ≤ B
X ≥ 0
Позначимо F = - Z.
Тоді max F= -min Z, і можна розв’язувати задачу (3.1)-(3.3)
3. Розглянемо пари симетричних задач.
F = C ∙ X"max (3.1) Z = Y ∙ B " min (3.4) (3.4)
A ∙ X ≤ B (3.2) Y∙A ≥ C (3.5) (3.5)
X ≥ 0 (3.3) Y ≥ 0 (3.6) (3.6)
де 
Кожна задача називається двоїстою стосовно іншої. Якщо вихідна задача (3.1)-(3.3) є задачею про оптимальний план випуску продукції, то двоїста (3.4)-(3.6) є задача про використання ресурсів.
yi- ціна (оцінка) відповідного ресурсу, а Z=Y∙ В - вартість усіх ресурсів.
Вихідна задача: скільки і якої продукції виробити, щоб при заданих обсягах ресурсів і цінах на продукцію забезпечити максимальний доход.
Двоїста задача: якою повинна бути ціна кожного з ресурсів, щоб за даних обсягів ресурсів і цінах на продукцію забезпечити мінімум усіх витрат.
Теорема. Якщо з пари двоїстих задач в одній є оптимальний план, то й інша має розв’язок, при цьому min Z=max F.
Якщо цільова функція однієї з задач не обмежена, то й інша не має розв’язку.
Теорема справедлива і для пари несиметричних задач:
F = С ∙ X ® max Z = Y ∙ У ® min
А ∙ X = В Y ∙ A ³ C
X  0
0
Умова невід’ємності для другої задачі відсутня.
Уведенням додаткових змінних пара симетричних задач перетворюється на пару несиметричних. Розв’язуючи більш просту задачу, можна одержати одночасно і розв’язок двоїстої задачі.
4. Приклад
Z = x1 + 2x2 + 3x3 ®min
 xj ³ 0; j = 1,2,3.
xj ³ 0; j = 1,2,3.
Складемо і розв’яжемо двоїсту задачу.
F = 2y1 + 3у2 + 6у3 + 3у4 ® max
 уi ³ 0; i = 1,2,3,4
уi ³ 0; i = 1,2,3,4
Уводимо додаткові змінні.

F = 2y1 + 3у2 + 6у3 + 3у4 +0×у5+0×у6+0×у7® max
| Базис | Сбаз | В | А1 | А2 | А3 | А4 | А5 | А6 | А7 | ||
| А5 А6 А7 | -1 | -1 | -2 | -2 | |||||||
| Fj - Cj | -2 | -3 | -6 | -3 | |||||||
| А3 | -1 | ||||||||||
| А6 |
| -1 | -1 | ||||||||
| А7 | |||||||||||
| Fj - Cj | -9 | ||||||||||
| А3 | 3/2 | 3/2 | 1/2 | 1/2 | |||||||
| А2 | ½ | -1/2 | -1/2 | 1/2 | |||||||
| А7 | -1 | ||||||||||
| Fj - Cj | 10,5 | 4,5 | 1,5 | 4,5 |
 План не є оптимальним F (Y0) = 0.
План не є оптимальним F (Y0) = 0.
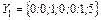 План не є оптимальним F (Y1) = 6.
План не є оптимальним F (Y1) = 6.
 План оптимальний F (Y2) = 10,5.
План оптимальний F (Y2) = 10,5.
Одержали розв’язок двоїстої задачі.
 ; Fmax = F (Y*) = 10,5.
; Fmax = F (Y*) = 10,5.
Для вихідної задачі Zmin = 10,5.
Оптимальний план вихідної задачі знаходимо у рядку оцінок останньої таблиці в стовпцях векторів, що входили в первісний базис: хj = Fj.
х1 = 1,5+0 = 1,5
х2 = 4,5+0 = 4,5 
х3 = 0+0 = 0 Zmin = Z (X*) = 10,5
Контрольні запитання
1. Як перетворити неканонічну ЗЛП у канонічну за допомогою додаткових змінних?
2. Яким є алгоритм розв’язування задач ЛП на мінімум цільової функції?
3. Що таке симетричні задачі ЛП?
4. Як виявляється двоїстість при розв’язуванні пари несиметричних задач ЛП?
Читайте також:
- I. Застосування похідної та інтеграла до роз’язування задач елементарної математики.
- А) Задачі, що розкривають зміст дій
- АВТОМАТИЗАЦІЯ РОЗВ’ЯЗУВАННЯ КОМПЛЕКСУ ЗАДАЧ З ОБЛІКУ ОСНОВНИХ ЗАСОБІВ ТА НЕМАТЕРІАЛЬНИХ АКТИВІВ
- Автоматизоване робоче місце (АРМ) бухгалтера: призначення, функції та його рівні
- Адвокатура в Україні: основні завдання і функції
- Адміністративна відповідальність: поняття, мета, функції, принципи та ознаки.
- Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
- Алгоритм розв’язання задачі
- Алгоритм розв’язання задачі
- Алгоритм розв’язання розподільної задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
| <== попередня сторінка | | | наступна сторінка ==> |
| Розглянемо задачу наступного вигляду | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |