• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Статистична обробка результатів

Виміри‚ обчислені за однакових умов‚ називають рівноточними. Центр групування результатів таких вимірювань визначає просте арифметичне середнє (22).

Коли немає систематичних похибок‚ то арифметичне середнє ряду рівноточних результатів вимірювань у міру їх необмеженого зростання наближається до справжнього значення величини‚ що вимірюється.

Водночас будь-яке значення параметра‚ обчисленого на підставі обмеженого обсягу вимірювань‚ завжди міститиме елемент випадковості. Таке наближене значення називають оцінюванням параметра. Наприклад‚ оцінкою для математичного сподівання (11) може бути середнє арифметичне змінної характеристики в n незалежних дослідах. Коли оцінка має таку властивість‚ що із збільшенням кількості дослідів n її значення наближається до точного значення величини‚ яка вимірюється‚ то її називаютьслушною‚ а коли немає систематичних похибок — незміщеною. Вибрана незміщена оцінка повинна мати найменшу дисперсію

. (27)

Оцінку‚ яка задовольняє (27)‚ називають ефективною.

Отже‚ оцінка для математичного сподівання - слушна і незміщена‚ бо із збільшенням n x®a. Дисперсія для такої оцінки

. (27а)

Коли розподіл нормальний‚ то дисперсія мінімальна‚ тобто оцінка ефективна. Оцінкою дисперсії є статистична дисперсія

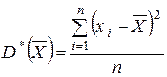. (28)

Як засвідчує перевірка цієї оцінки‚ для скінченних значень n‚ тобто коли обсяги вибірки невеликі‚ вона неслушна і є зміщеною оцінкою .

Відповідну незміщену оцінку обчислюють таким чином:

. (29)

Обсяг вибірки‚ від якого залежить можливість використання співвідношень (28) або (29) ‚ дуже не визначений і зумовлений багатьма причинами: необхідною точністю вимірювань‚ умовами проведення випробувань‚ якістю використовуваних приладів тощо.

Вважають‚ що для вимірювання властивостей будівельних матеріалів і конструкцій вираз (29) потрібно застосовувати‚ коли n>30. Проте ця величина умовна й може змінюватися залежно від змісту досліджень.

У багатьох випадках обробки результатів спостережень доводиться мати справу з нерівноточними вимірами‚ які виникають‚ коли вимірювання зроблено різними приладами чи інструментами‚ в різних умовах або навіть різними дослідниками. Тому окремим відлікам узвичаєно надавати різної ваги u_i‚ яка може бути довільною‚ але обов’язково обґрунтованою. Якщо відомі точності приладів або відмінність у їх базах‚ то можна вибрати вагу пропорційно до цих даних. Коли ж про прилади та умови нічого невідомо‚ то вагу природно вибрати пропорційно до кількості однорідних вимірювань n_i та дисперсії s_i² (звісна річ‚ коли кожна серія підлягає нормальному законові розподілу). Тоді

. (30)

У цьому разі найімовірніше значення шуканої величини можна визначити як середнє значення серії нерівноточних вимірів

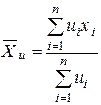. (31)

Очевидно‚ середньоквадратичне відхилення середньозваженої оцінки сталої величини для скінченого n

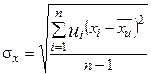. (32)

Наведені оцінки точності результатів вимірювань називають точковими.

При статистичному аналізі важливою задачею є визначеннянадійногоінтервалу‚ виходу за його межі вимірюваної величини x_i ‚ яка внаслідок випадкових коливань має ймовірність меншу‚ ніж та‚ що задана.

Для оцінки інтервалу при обмеженій кількості дослідів використовують розподіл Стьюдента

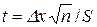‚ (33)

звідси .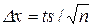

При заданій надійності p вимірювана величина потрапляє в інтервал

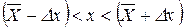. (34)

Висунуту статистичну гіпотезу безпосередньо за вибірковими даними перевіряють за допомогою критеріїв згоди.

Коли обсяг вибірки невеликий (n<30)‚ то нормальність розподілу можна перевірити за допомогою асиметрії А та ексцесу Е.

Для строгого нормального розподілу А=0 і Е=0. У яких межах можуть коливатися ці величини – питання неоднозначне. У багатьох літературних джерелах їх наведено так:

3 £ А £ 7 і -2£ Е £ 7.

Коли одержані результати вийшли за ці межі‚ гіпотезу нормального розподілу потрібно відкинути. Коли n велике‚ то нормальність розподілу перевіряють за критерієм Колмогорова чи c² – розподілом Пірсона.

Послідовність обробки результатів вимірювань за нормальним законом розподілу випадкової величини наведено на схемі рис.5.

Рис. 5. Обробка результатів вимірювань

за нормального закону розподілу випадкових величин

Читайте також:

1. II. Обробка результатів
2. III. Економічна інтерпретація результатів статистичного дослідження банків
3. Абсолютні та відності показники результатів діяльності підприємства.
4. Аналіз одержання результатів. Висновки рекомендації.
5. Аналіз отриманих результатів
6. Аналіз отриманих результатів, прийняття рішення про можливість видачі сертифікату відповідності
7. Аналіз результатів за відхиленнями
8. Аналіз результатів національного виробництва.
9. Аналіз результатів практичної діяльності Київського освітньо-методичного центру соціальної роботи
10. АНАЛІЗ РЕЗУЛЬТАТІВ ТЕРМОМЕТРІЇ
11. Аналіз рівня, динаміки та структури фінансових результатів підприємства
12. Аналіз складу і структури фінансових результатів підприємства

Переглядів: 1476