
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Основи кінематики поступального руху
Рух одного і того самого тіла відносно інших тіл можна охарактеризувати по-різному.
Оскільки механічний рух відбувається у просторі та у часі , то для повного опису руху потрібно знати розміщення тіла , або його частин , в будь-який момент часу. Для цього з тілом відліку зв’язують систему координат і годинник.
Тіло відліку, із відповідно зв’язаною системою координат і годинником для вимірювання проміжку часу , утворюють єдину систему відліку.
Система координат– це набір масштабів , за допомогою яких фіксується розміщення рухомих тіл. На практиці здебільшого користуються прямокутною системою координат.
а). Декартова система координат :
z
М ( x,y,z )
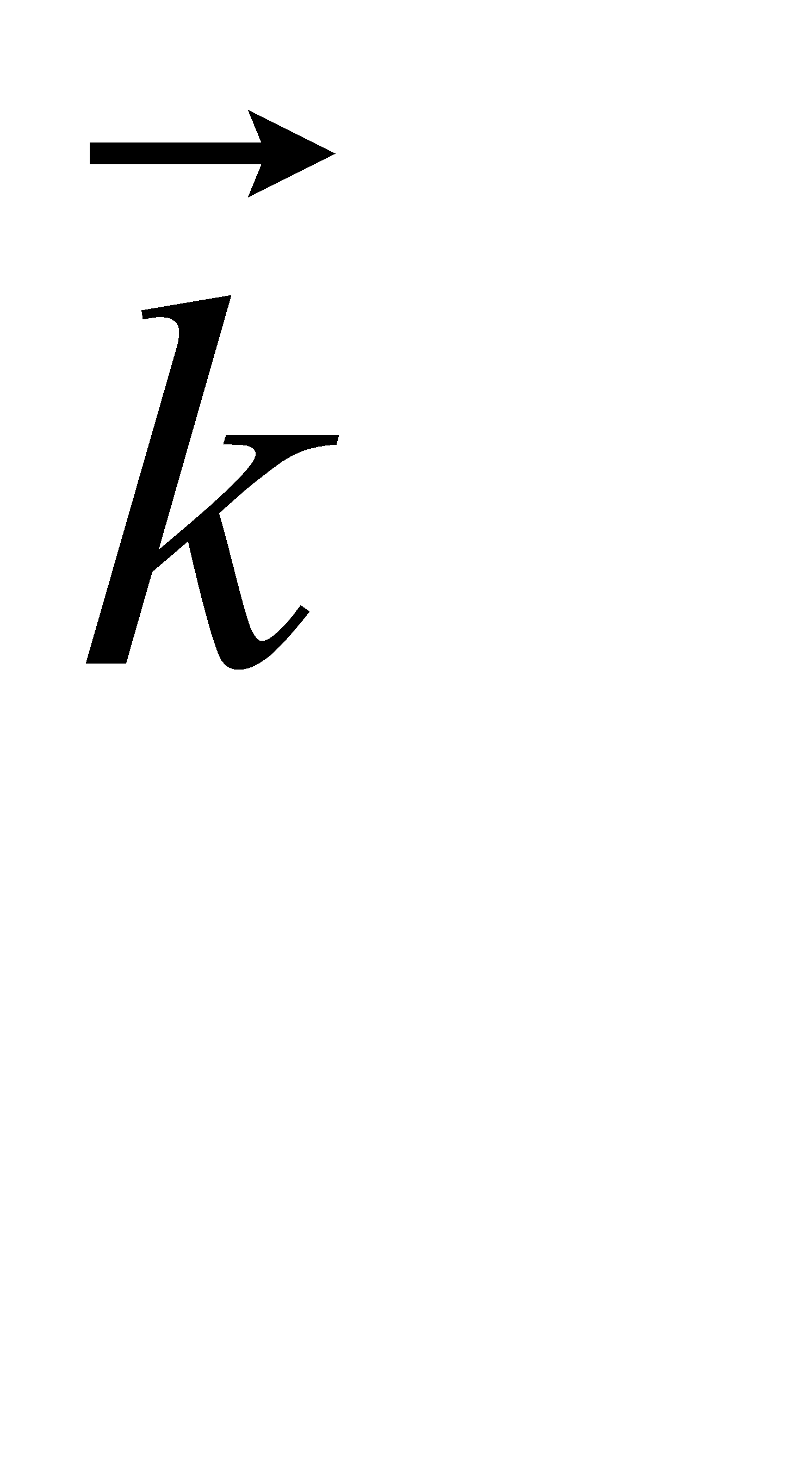
| у |
| O |
3 zbUpa5LSZFv992ZP8/FwDt/5ytVkenHk0XfOIsxnCQi2jVOdbRG+Puu7BQgfyCrqnWWEX/awqq6v SiqUO9kPPm5DKyLE+oIQdAhDIaVvNBvyMzewjd2PGw2FGMdWqpFOEW56mSbJvTTU2figaeBHzc1+ ezAI62yfk9zIp/rlfdB1+vy6efsOiLc30/oBROApXMZw1o/qUEWnnTtY5UWPsJxncYmQLkGc62yR g9gh5EkGsirlf//qDwAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAA AAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsA AAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAHotJTSzAgAAowUAAA4A AAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAHEiK6vcAAAABwEA AA8AAAAAAAAAAAAAAAAADQUAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAAAWBgAAAAA= " strokeweight=".26mm"> x
б). В сферичних (полярних) координатах положення точки задається величинами ρ, θ, φ , де ρ – абсолютне значення вектора 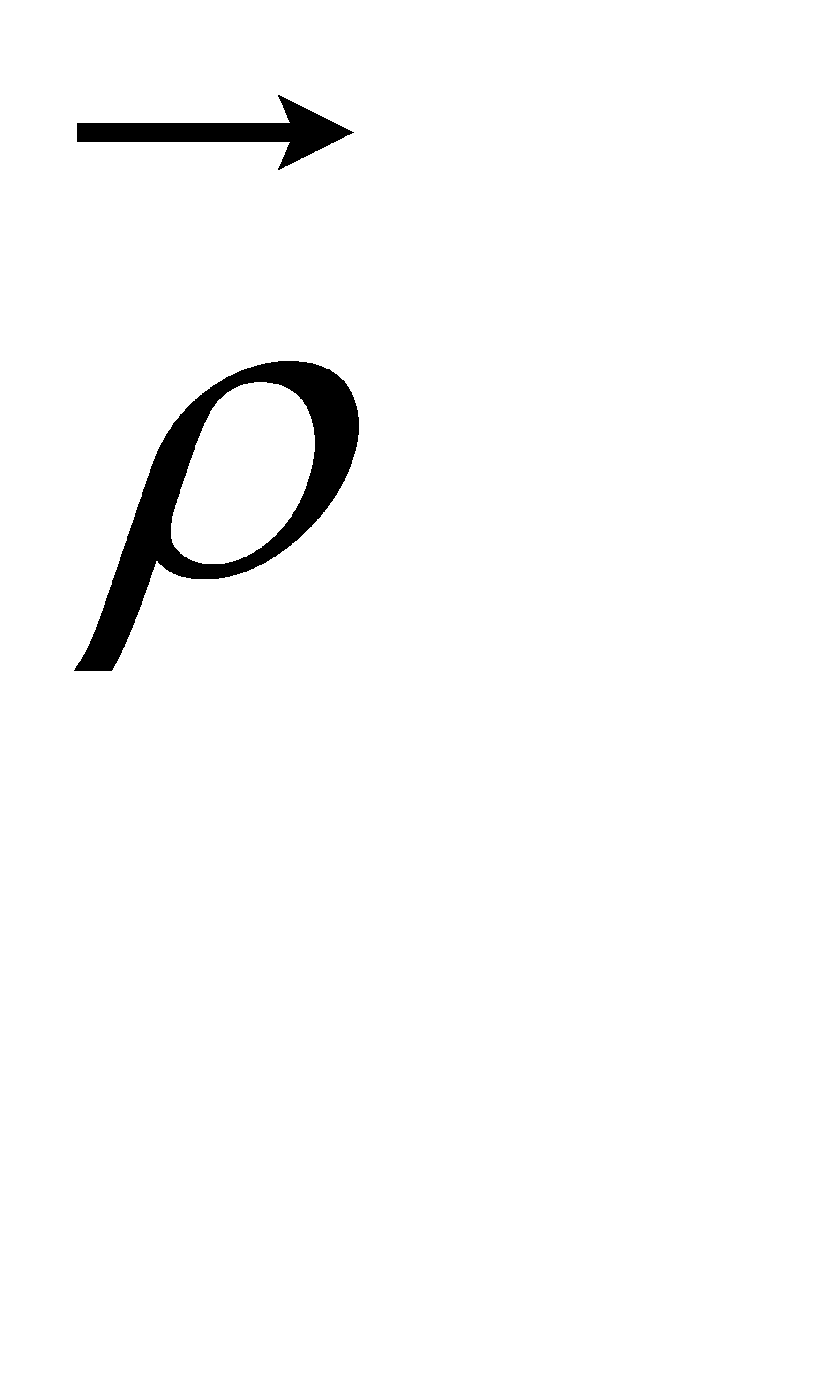 .
.
| Декартові координати зв’язані із сферичними наступним чином : |
z
| x = ρ sin θ cosφ y = ρsinθ sinφ z = ρcosθ |
θ 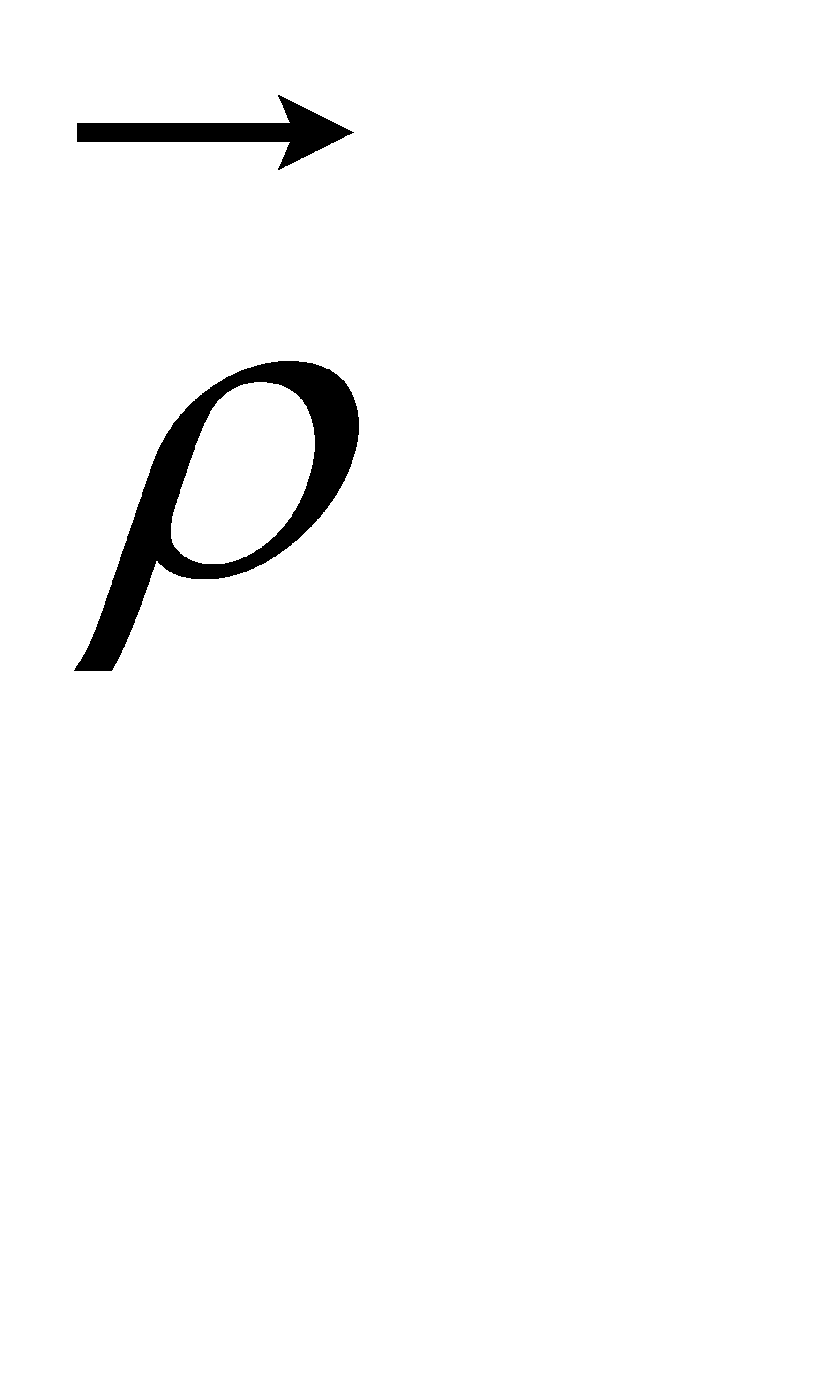
o
 φ y
φ y
x
в). Циліндрично-полярні координати ρ, φ, z.
| ox – полярна вісь ; ρ, φ – полярні координати ; z – апліката ; x = ρ cosφ y = ρ sinφ z =z |
z
M
| Z |
o
 φ y
φ y
ρ
x
Якщо відома часова залежність координат матеріальної точки , то можна визначити як вона буде рухатись. Лінія , яку описує матеріальна точка в просторі під час руху, називається траекторією руху.
Рівняння траекторії : ¦(x y z) = 0
Якщо траекторія – пряма лінія , то такий рух називають прямолінійним, а якщо крива – криволінійним.
Найпростішим прикладом криволінійного руху є рух матаеріальної точки по колу :
| Характер траекторії залежить від системи відліку. |
M
М
o
x
| о |
| х |
y = r(1-cosφ).
Положен ня матеріальної точки в просторі можна задати за допомогою радіус-вектора .
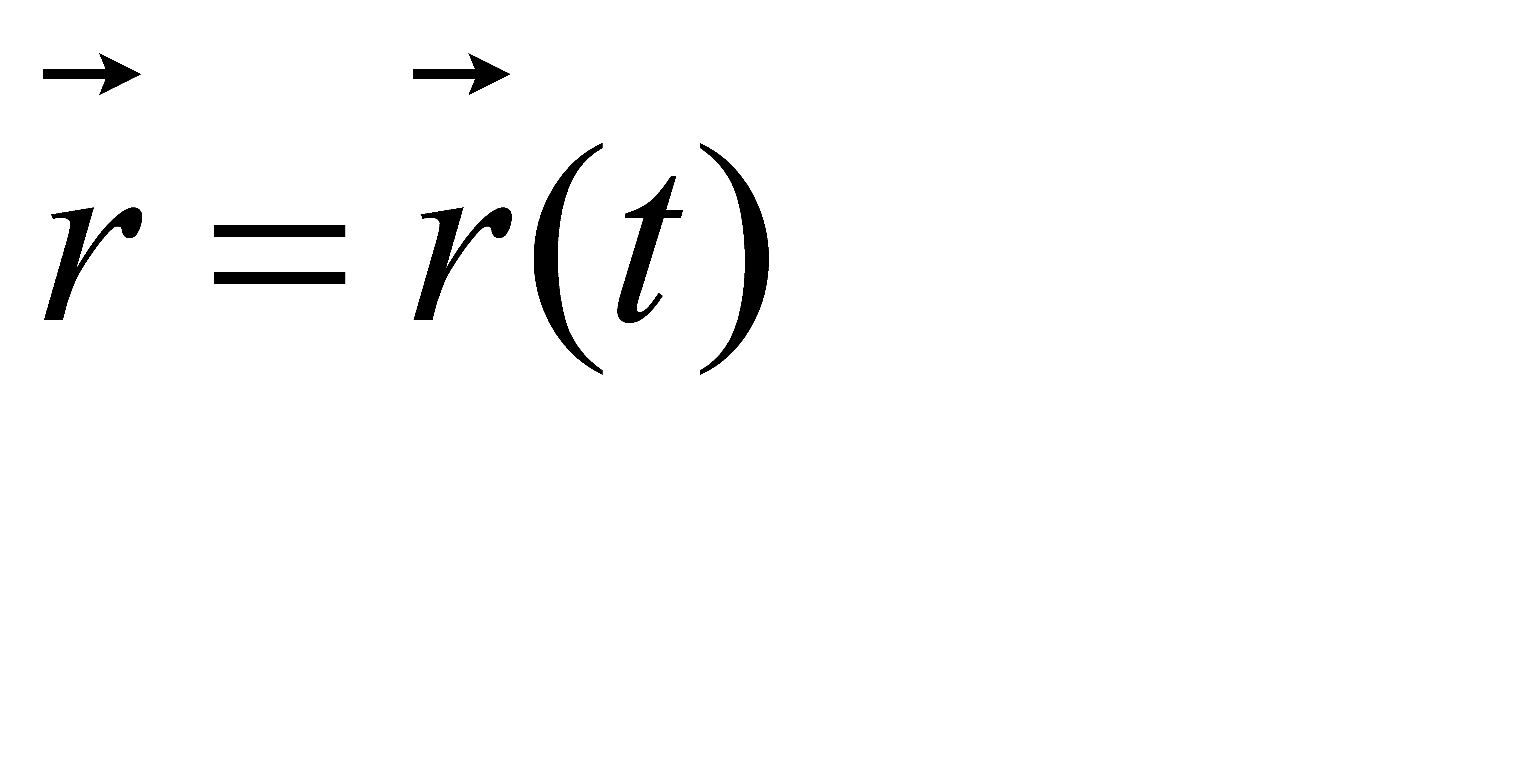 = x +y +z .
= x +y +z .
 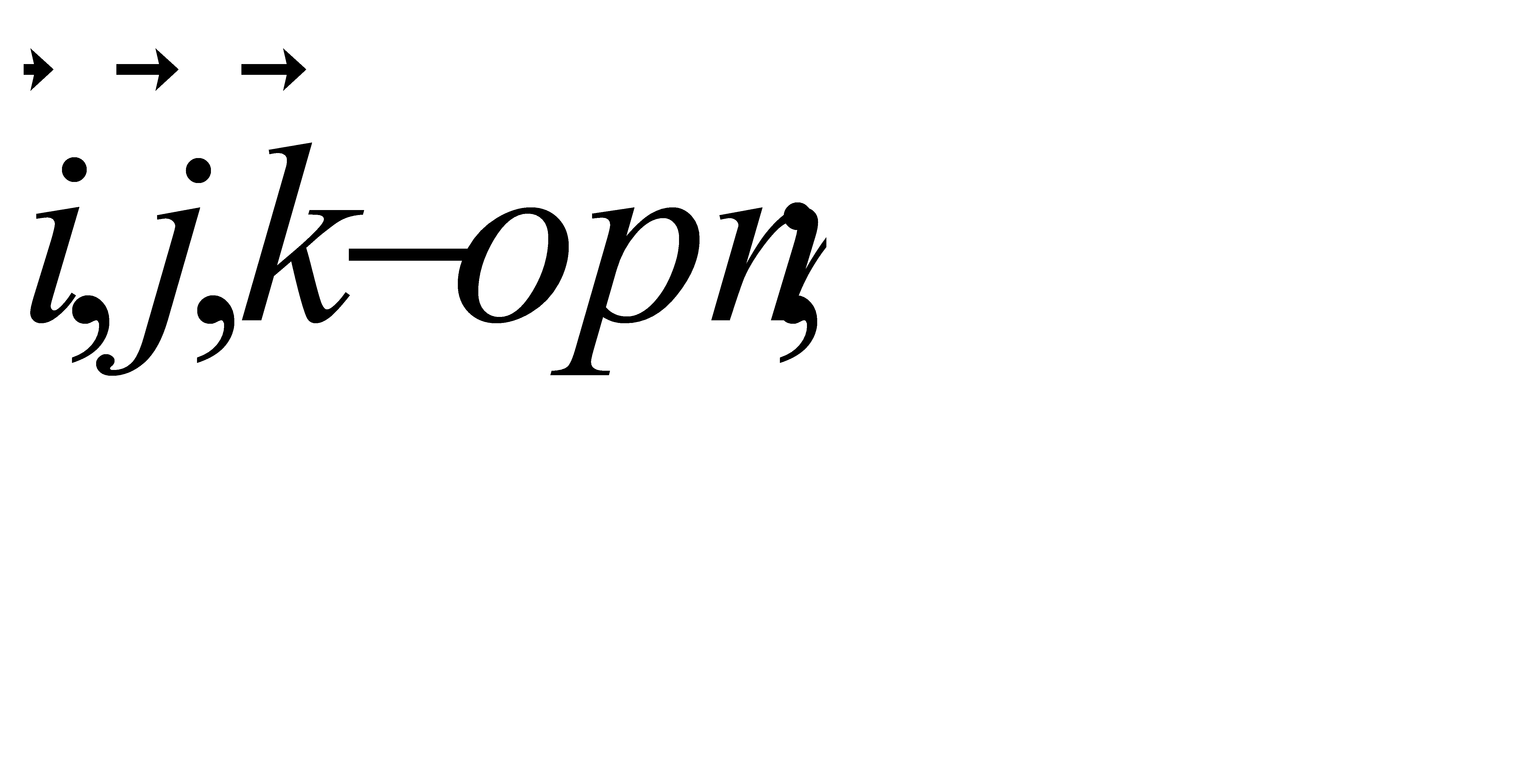 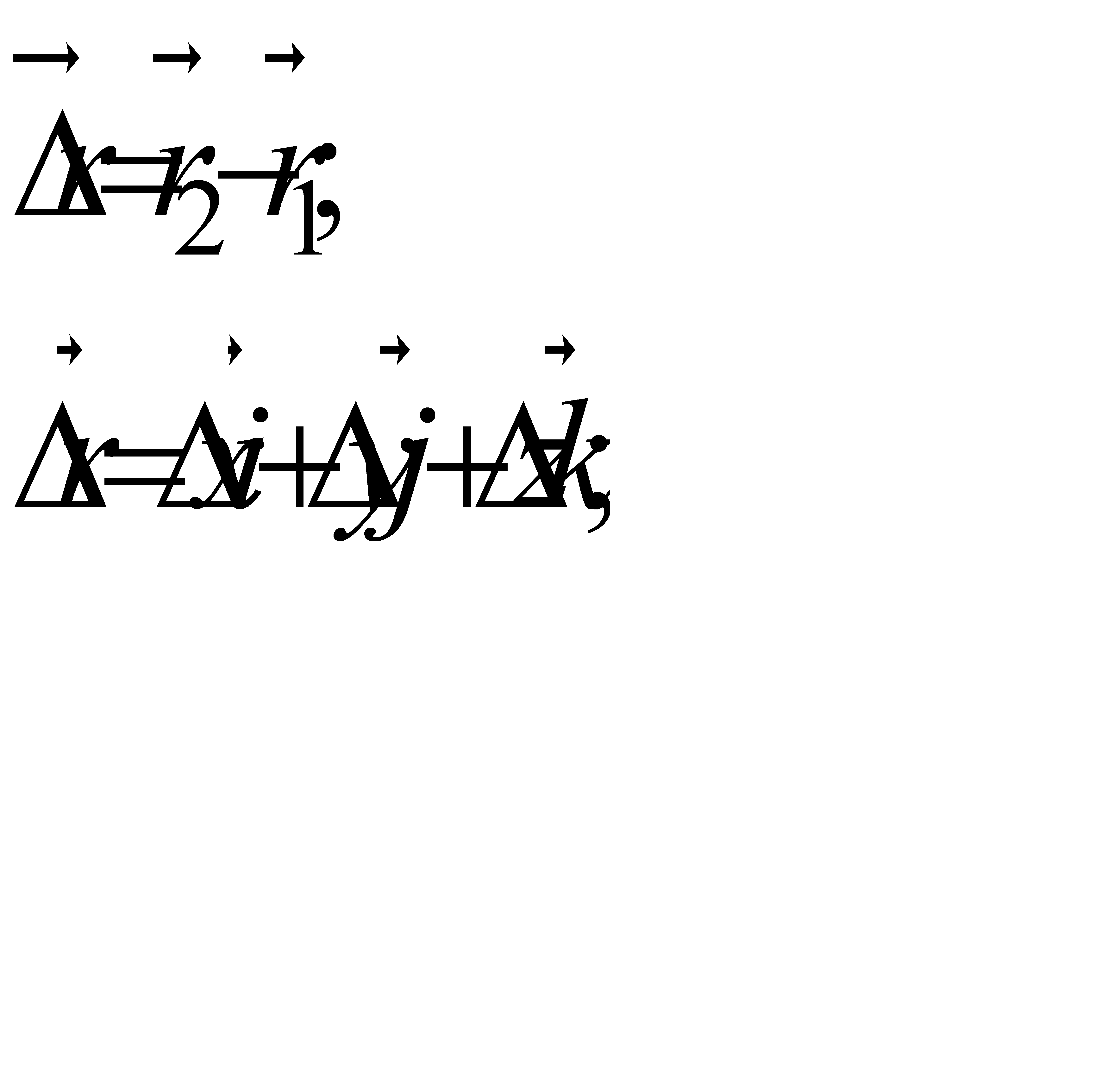
|
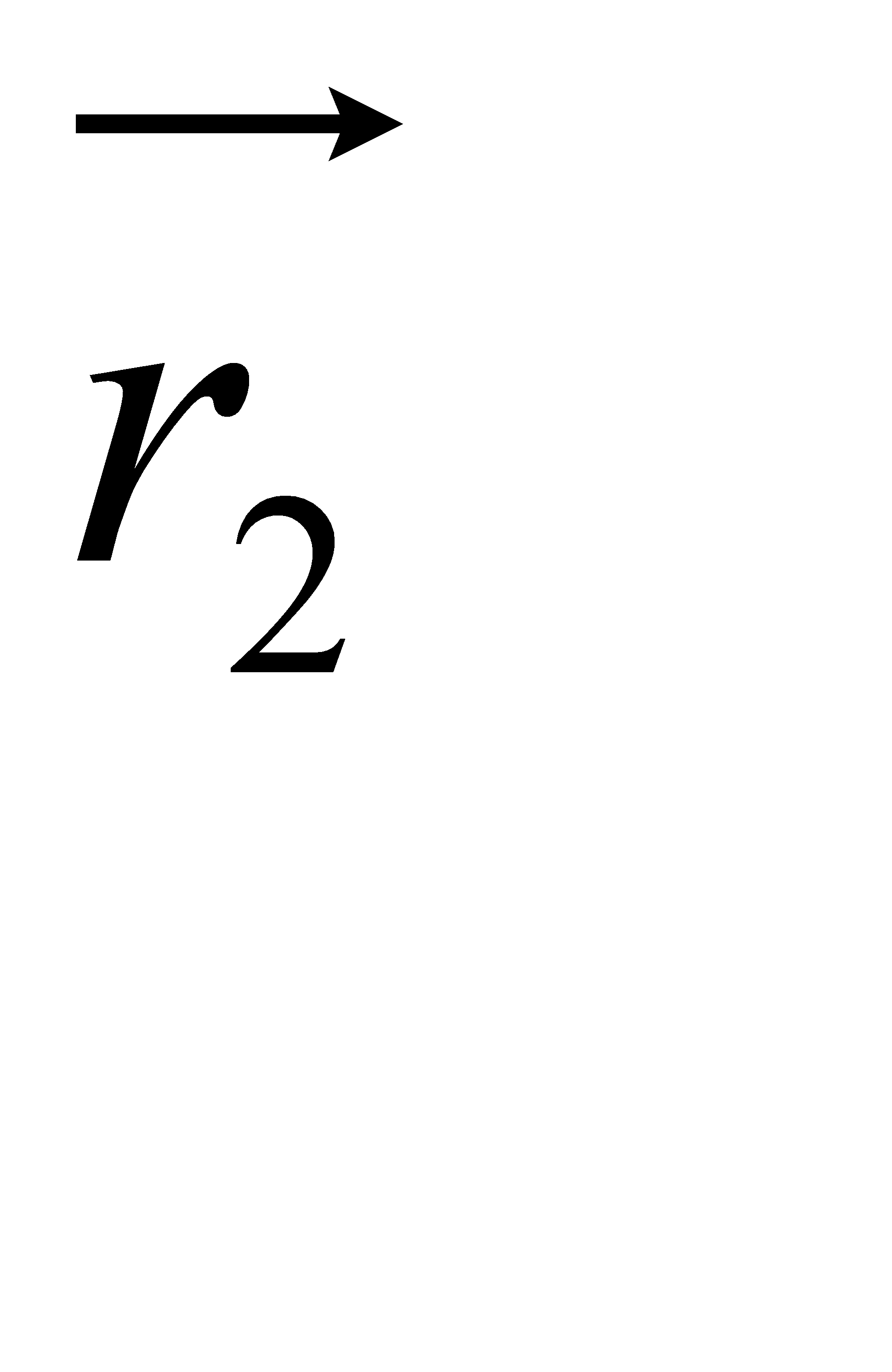
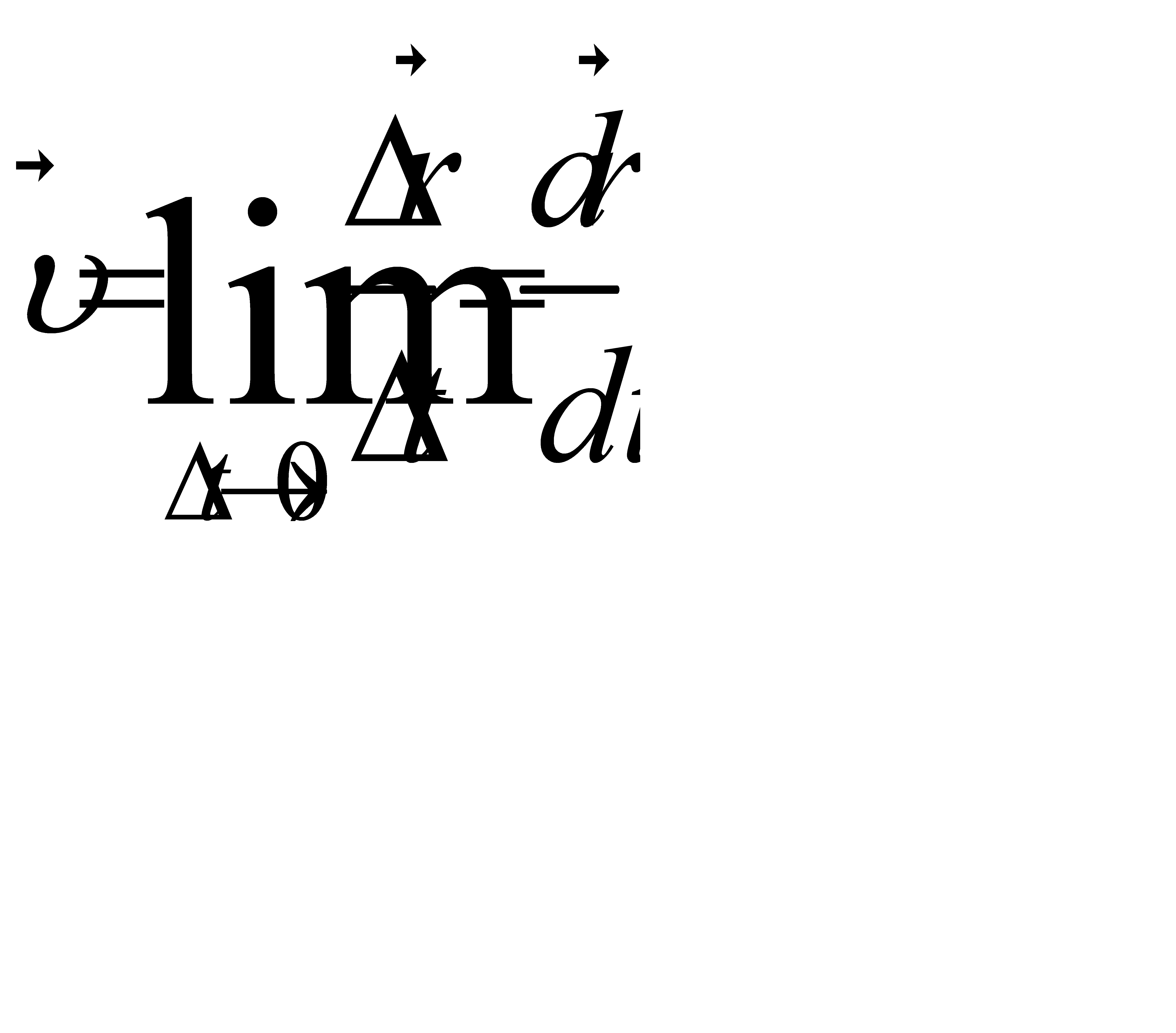
ΔS
z

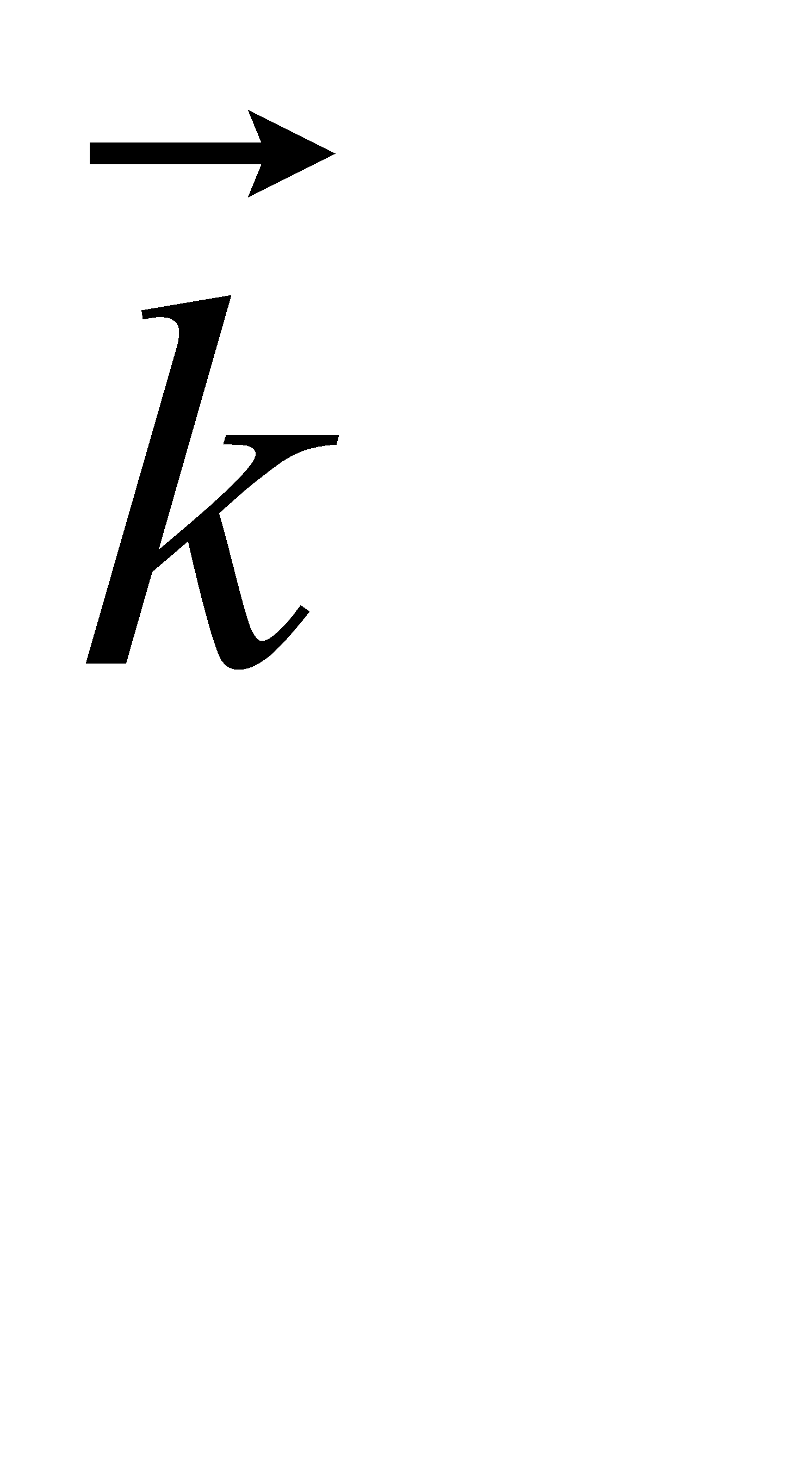
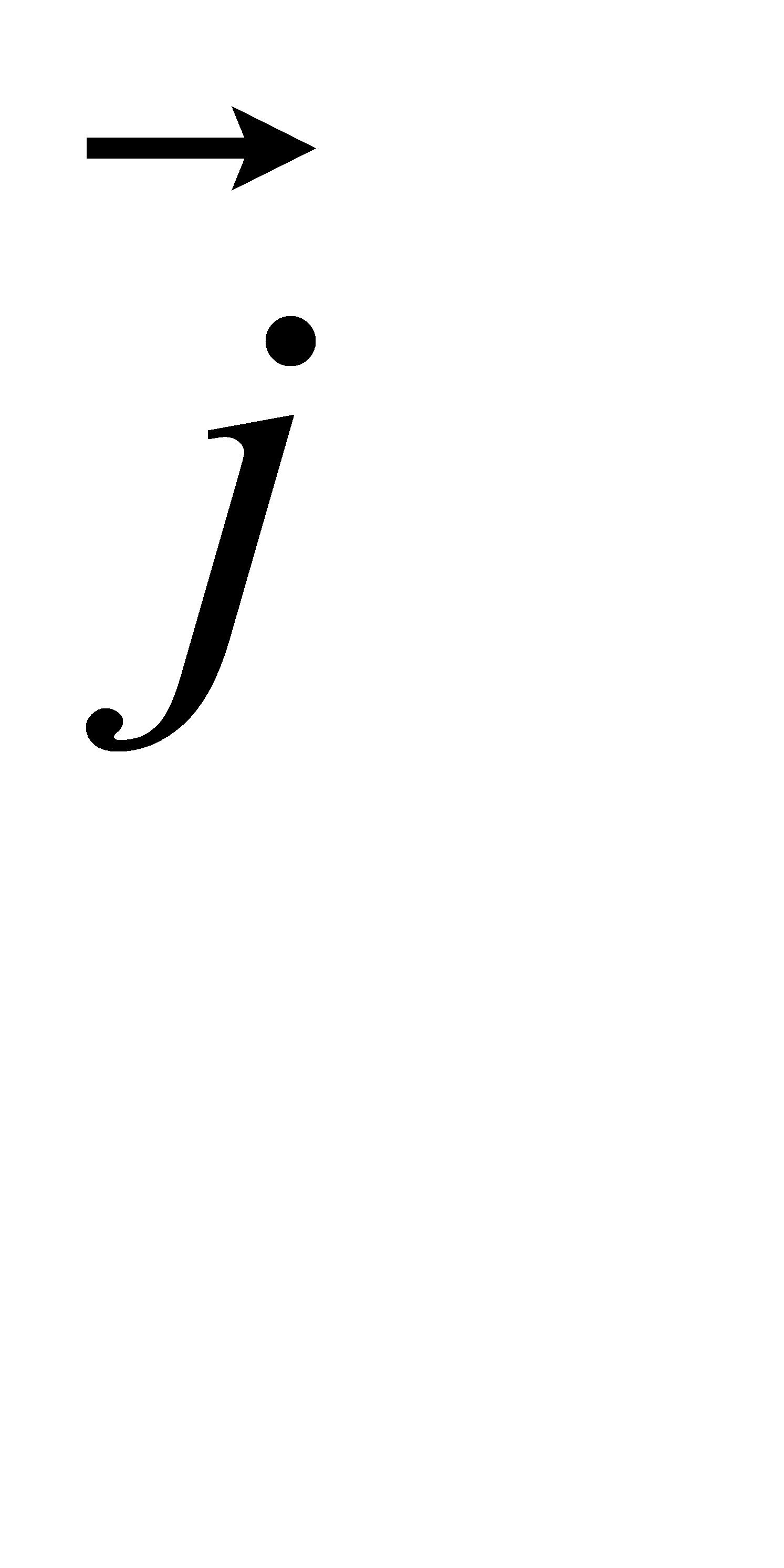
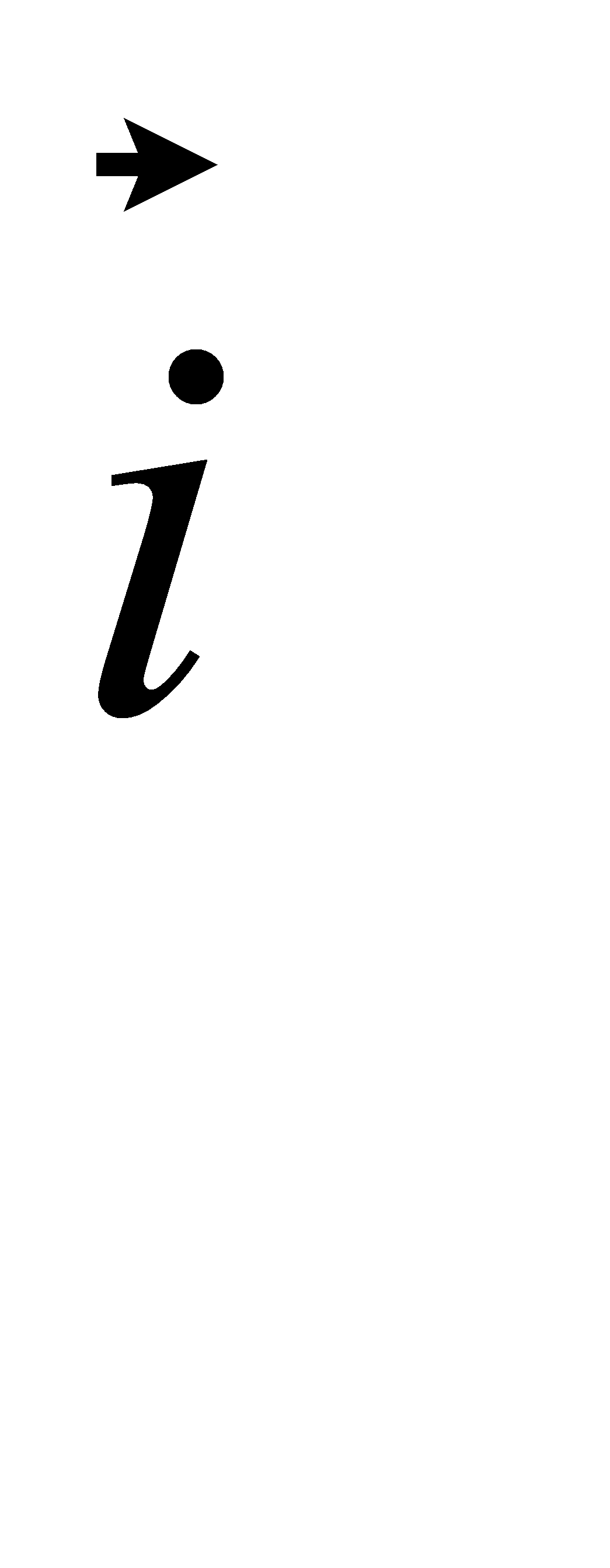
x
ΔS-шлях , пройдений точкою за Δt ;
При прямолінійному русі Δr = Δ S
При русі точки по колу за один оберт Δr = 0 , тоді як ΔS = 2pR
Будь-який складний рух тіла можна розкласти на два простих : поступальний та обертальний.
Основними кінематичними величинами , що характеризують рух точки є швидкість та прискорення.

Фізична величина , яка визначається
 , зветься середньою
швидкістю матеріальної точки.
Вектор , зветься середньою
швидкістю матеріальної точки.
Вектор 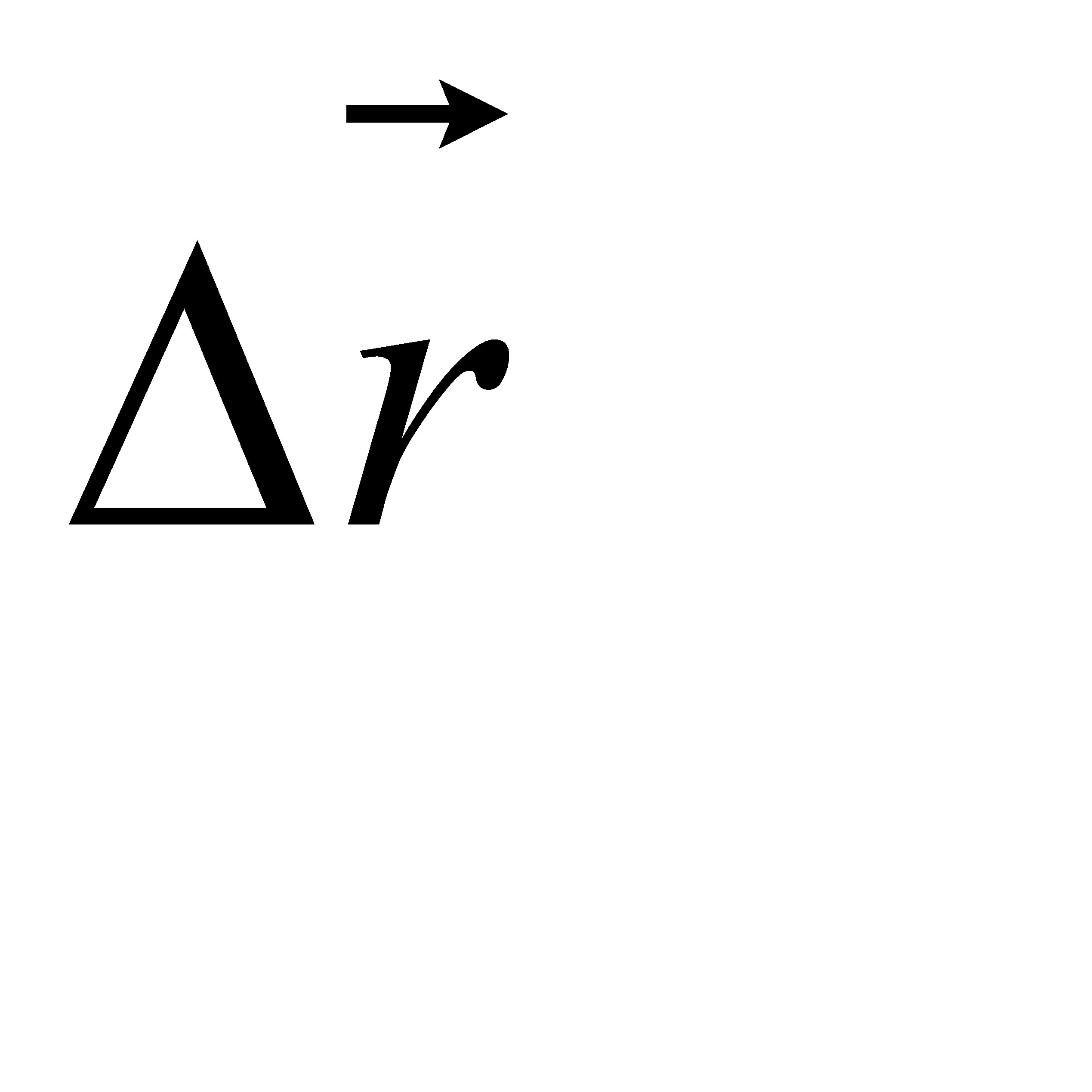
|
| |
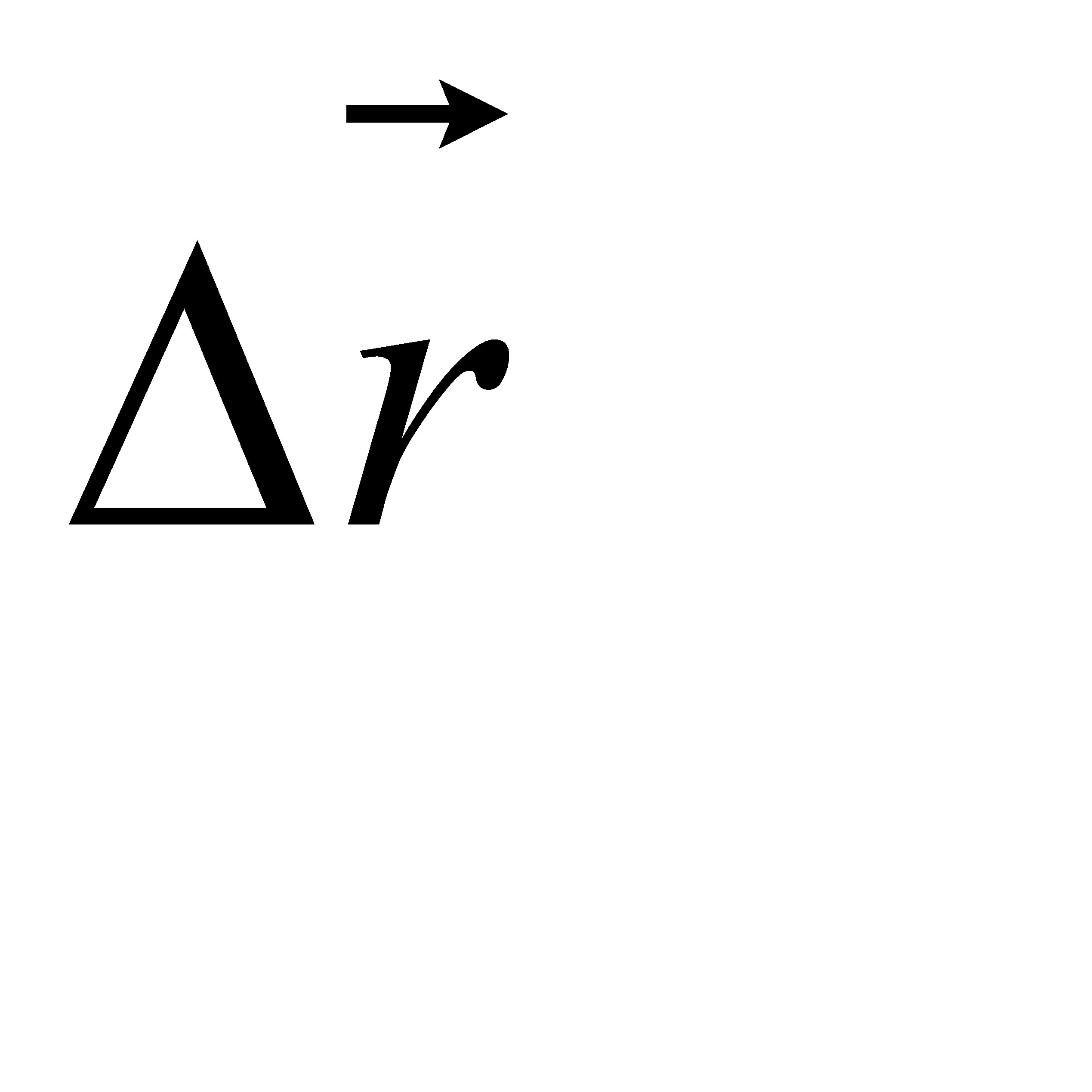
|
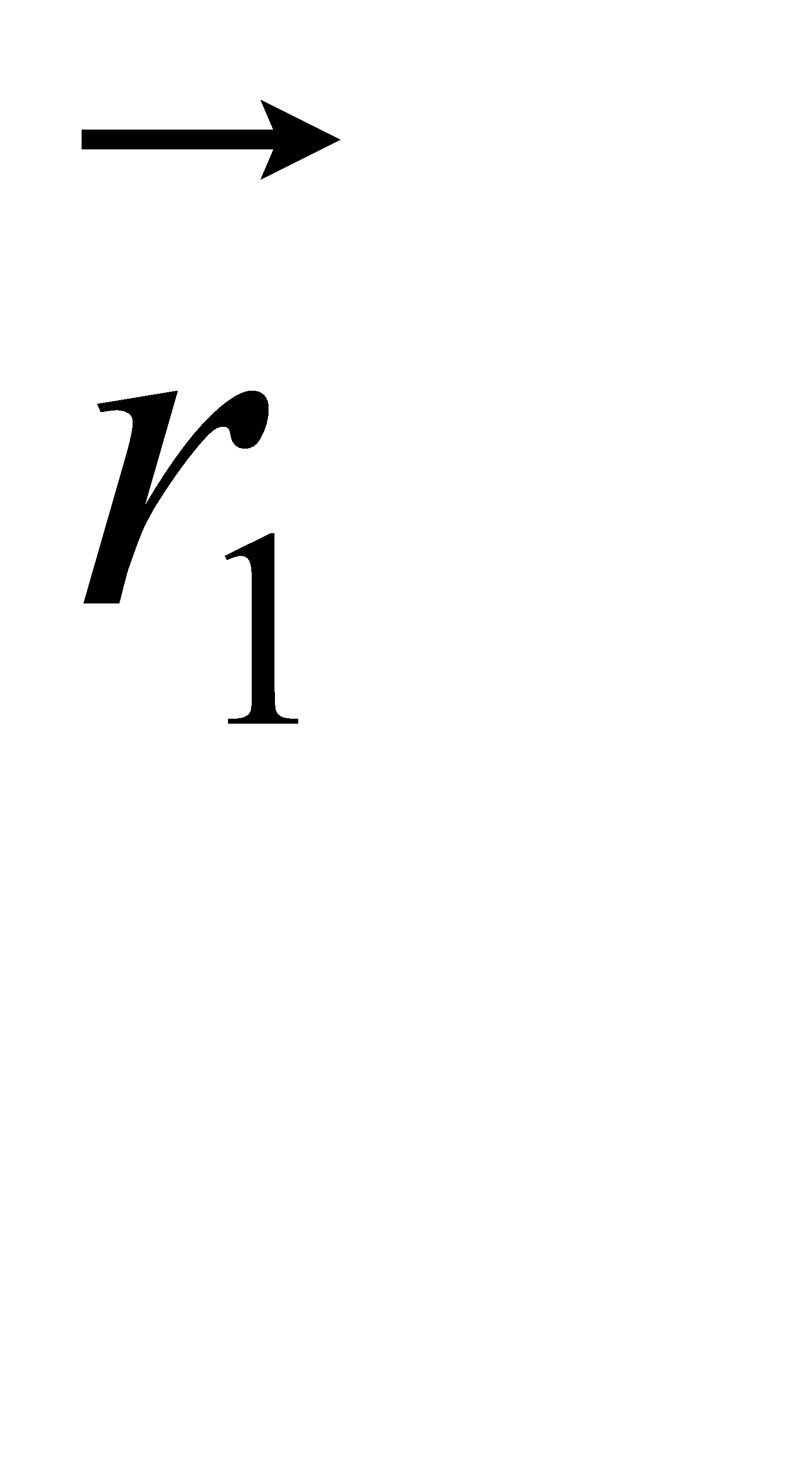
|
 Миттєва швидкість:
Миттєва швидкість:
υ
Вектор 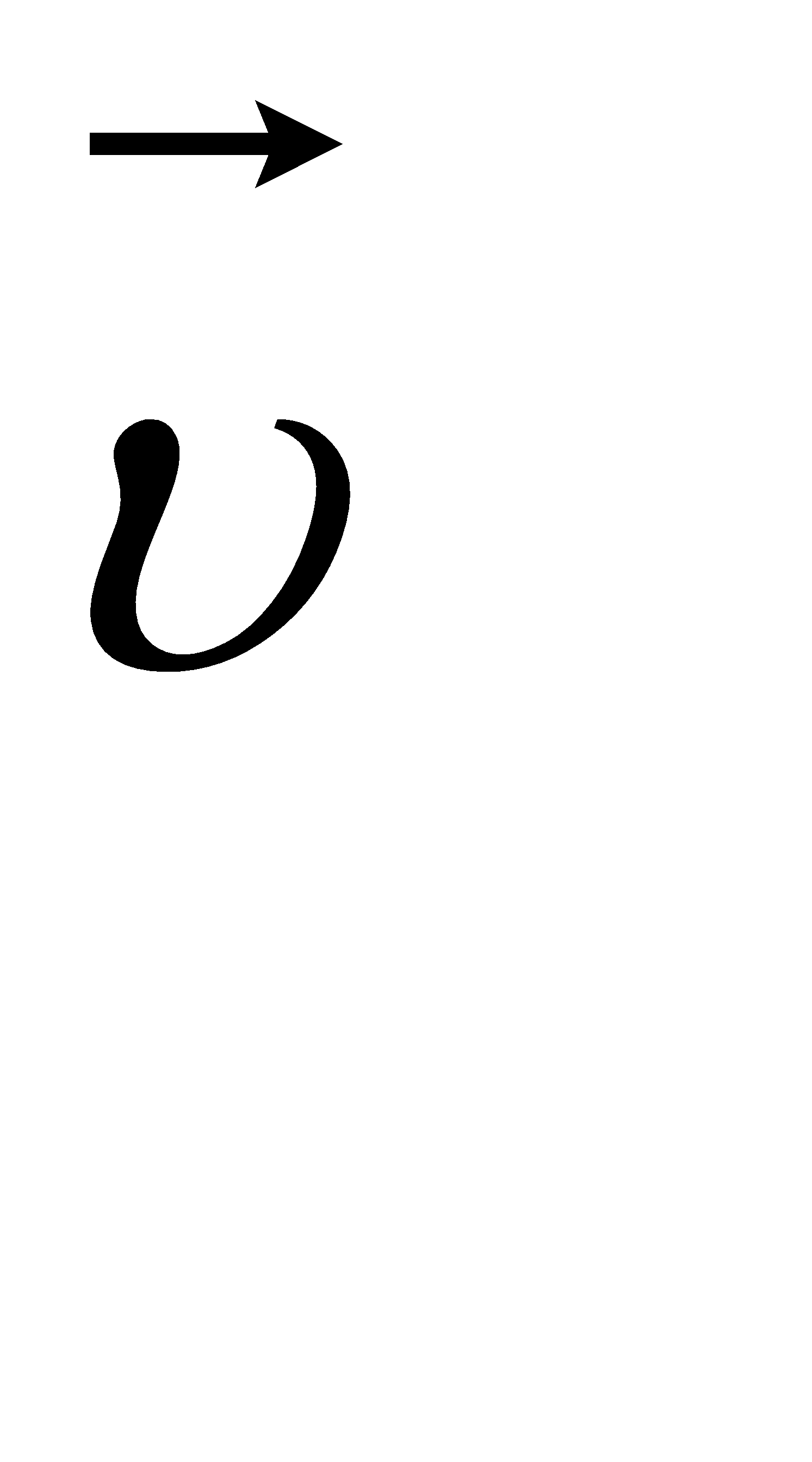 – спрямований по дотичній в напрямку руху.
– спрямований по дотичній в напрямку руху.
r Оскільки 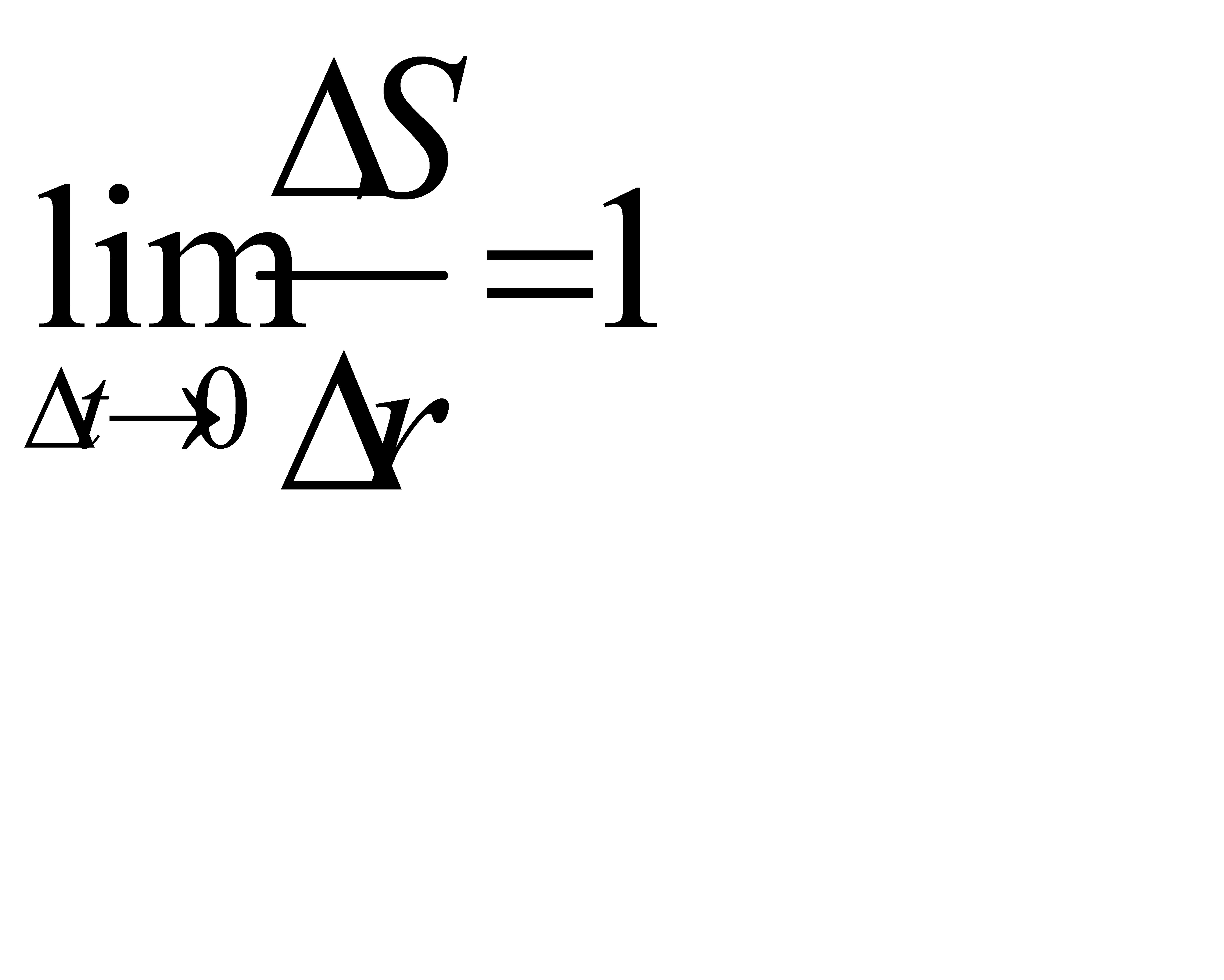 , то
, то 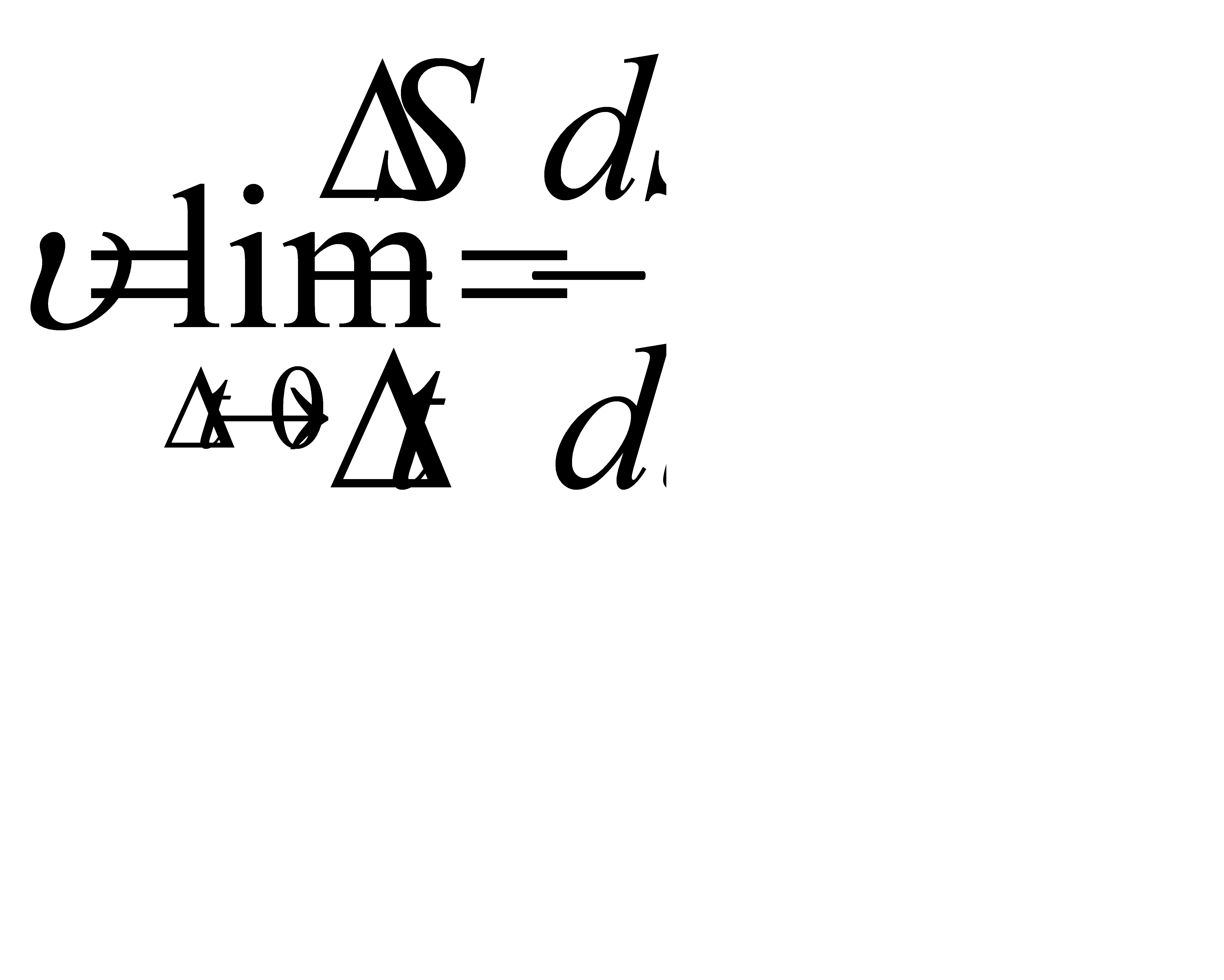 , тобто
, тобто
модуль швидкості υ дорівнює похідній від шляху по часу.
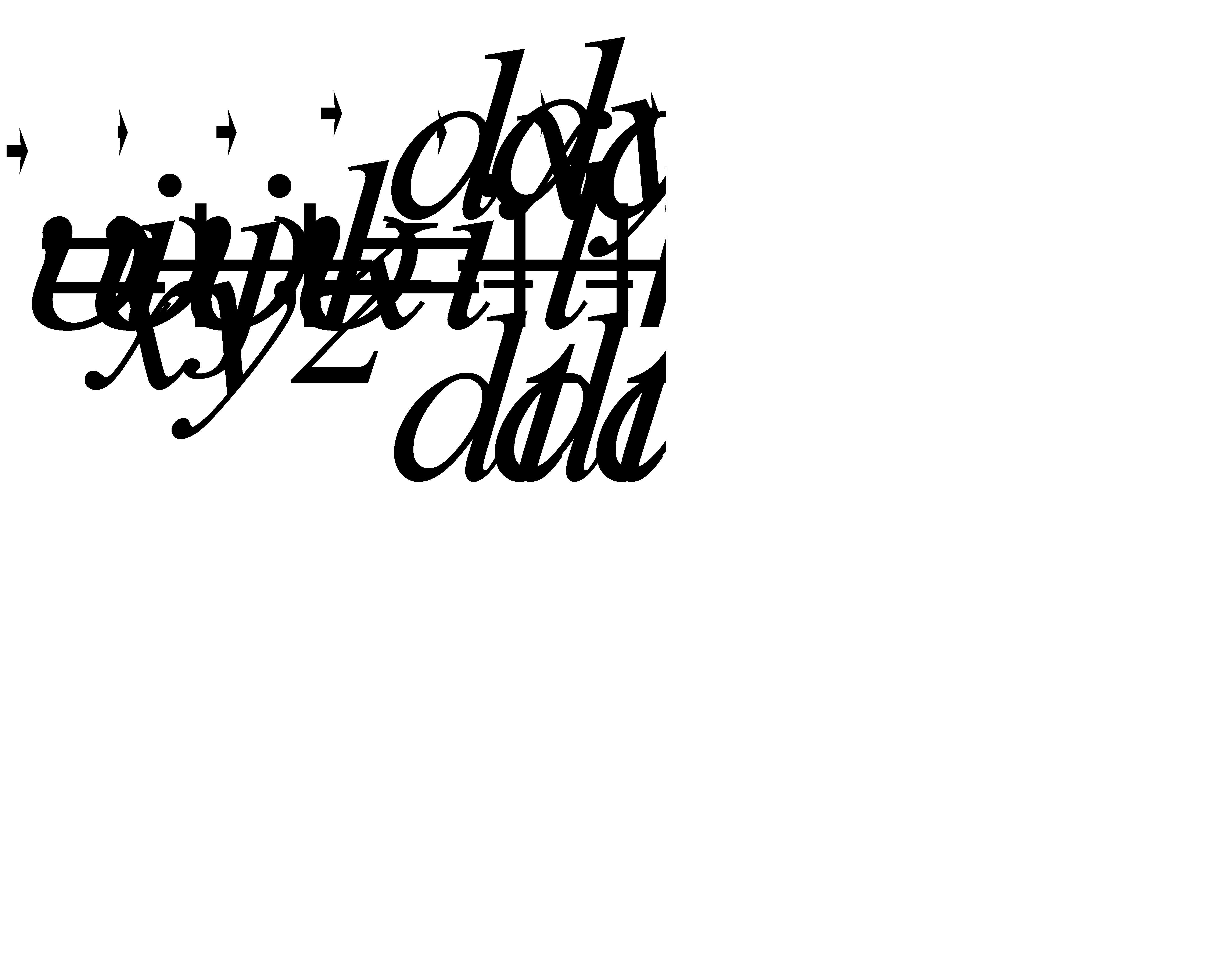 ,
,

Величина , що характеризує зміну швидкості за проміжок часу Δt називається середнім прискоренням :
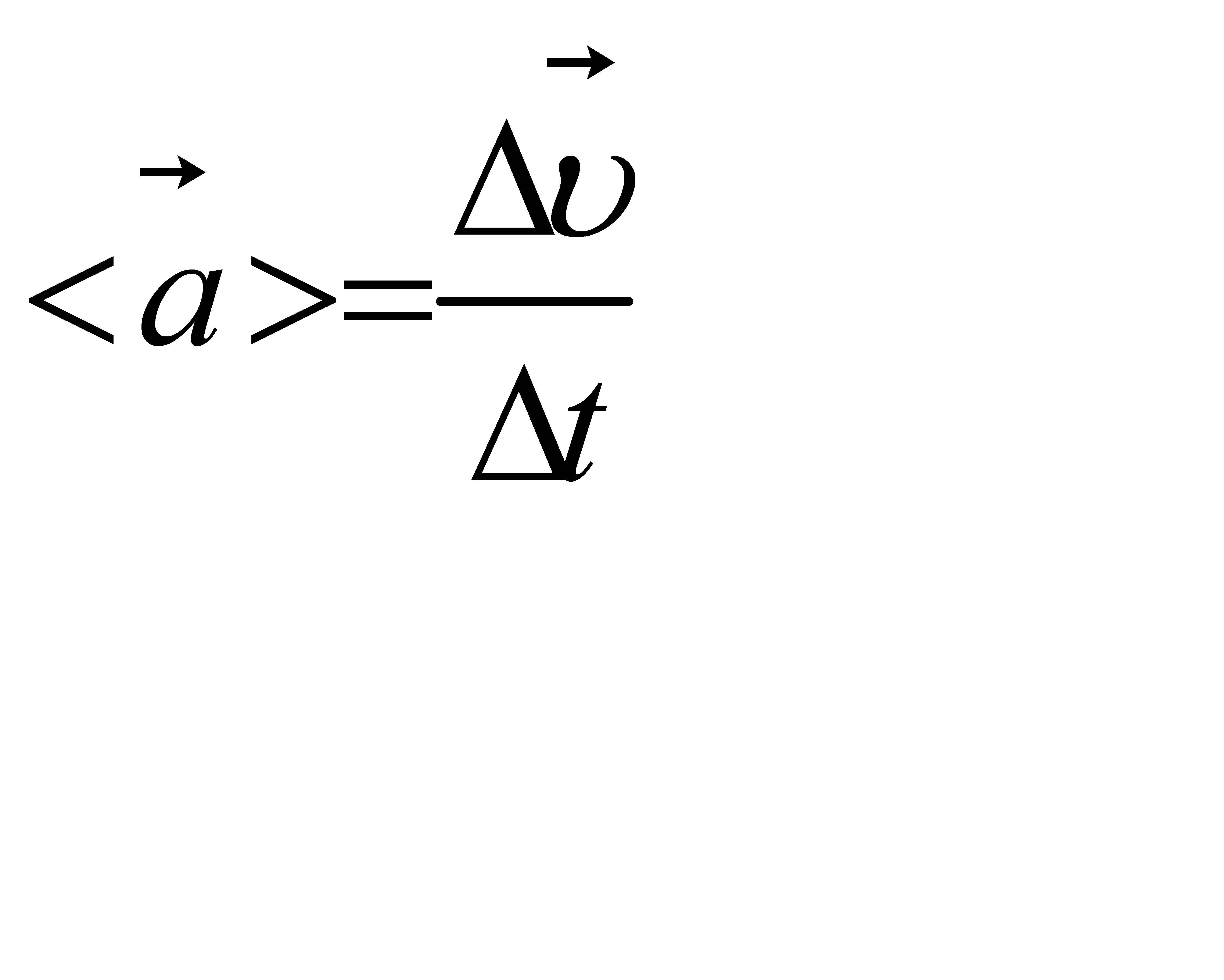 .
.
Миттєве прискорення визначається :
 ,
,
або 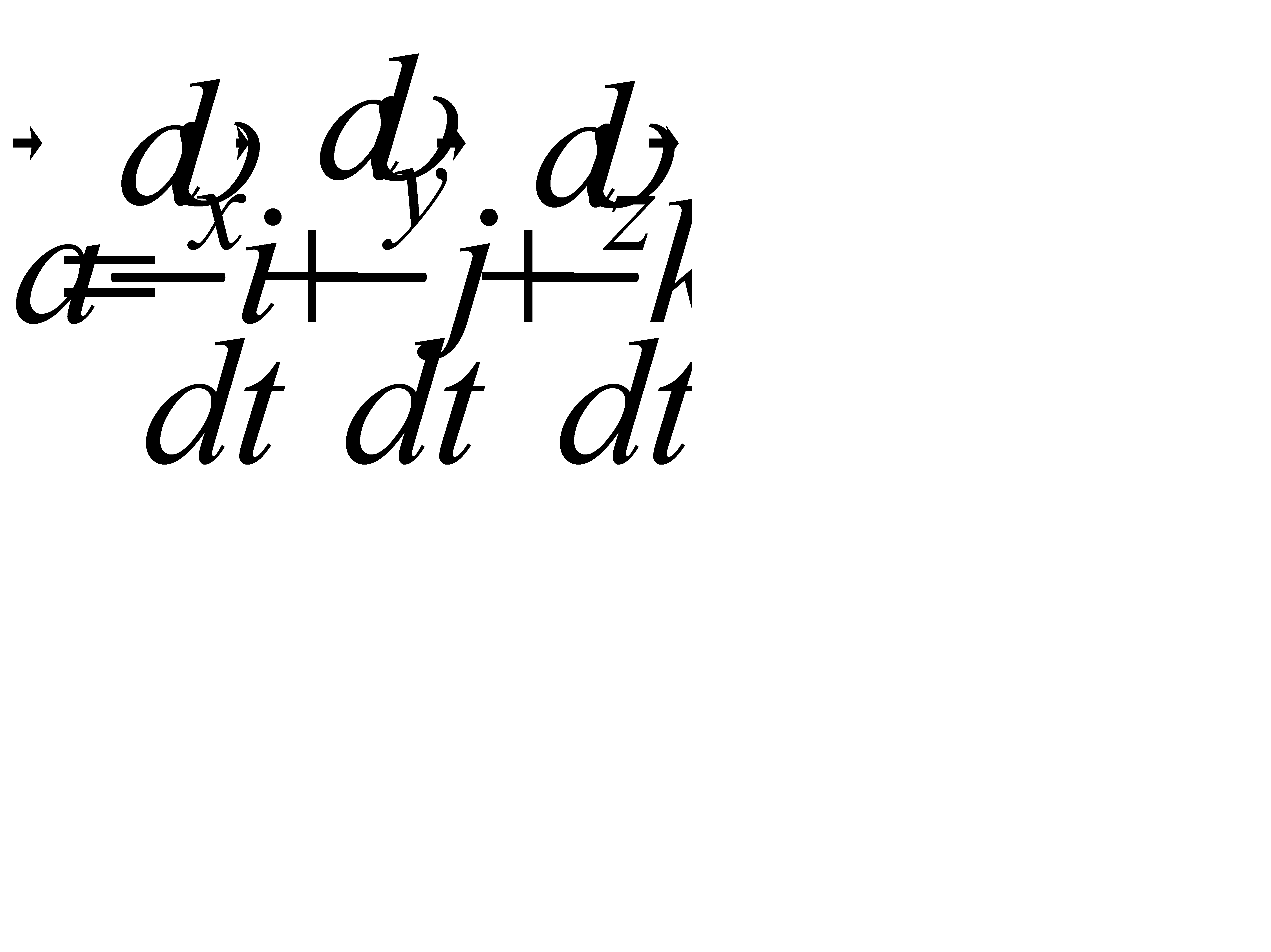 .
.
Вектор  спрямований туди , куди і
спрямований туди , куди і  ;
;
Вектор 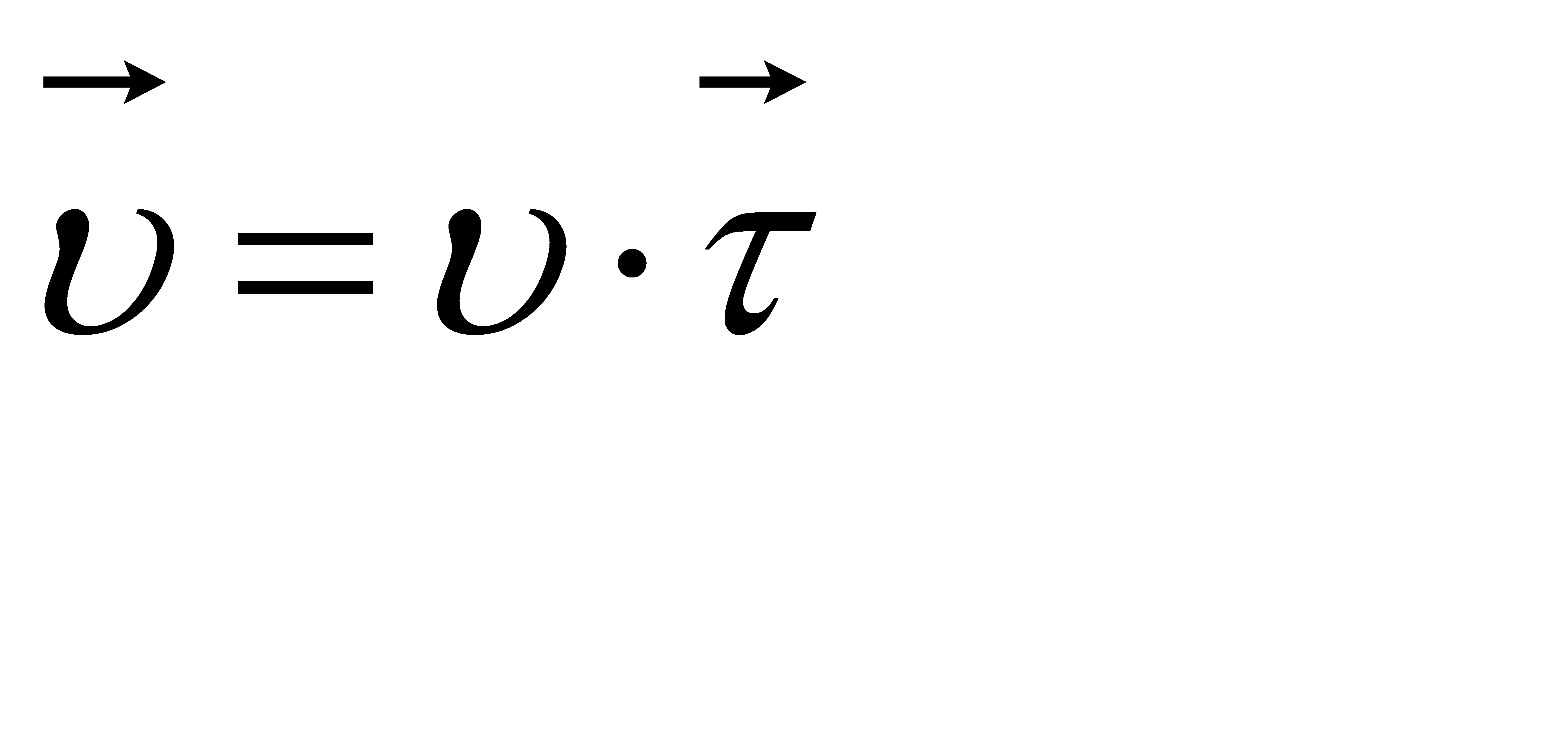 , де
, де  - одиничний дотичний вектор ; Тому
- одиничний дотичний вектор ; Тому
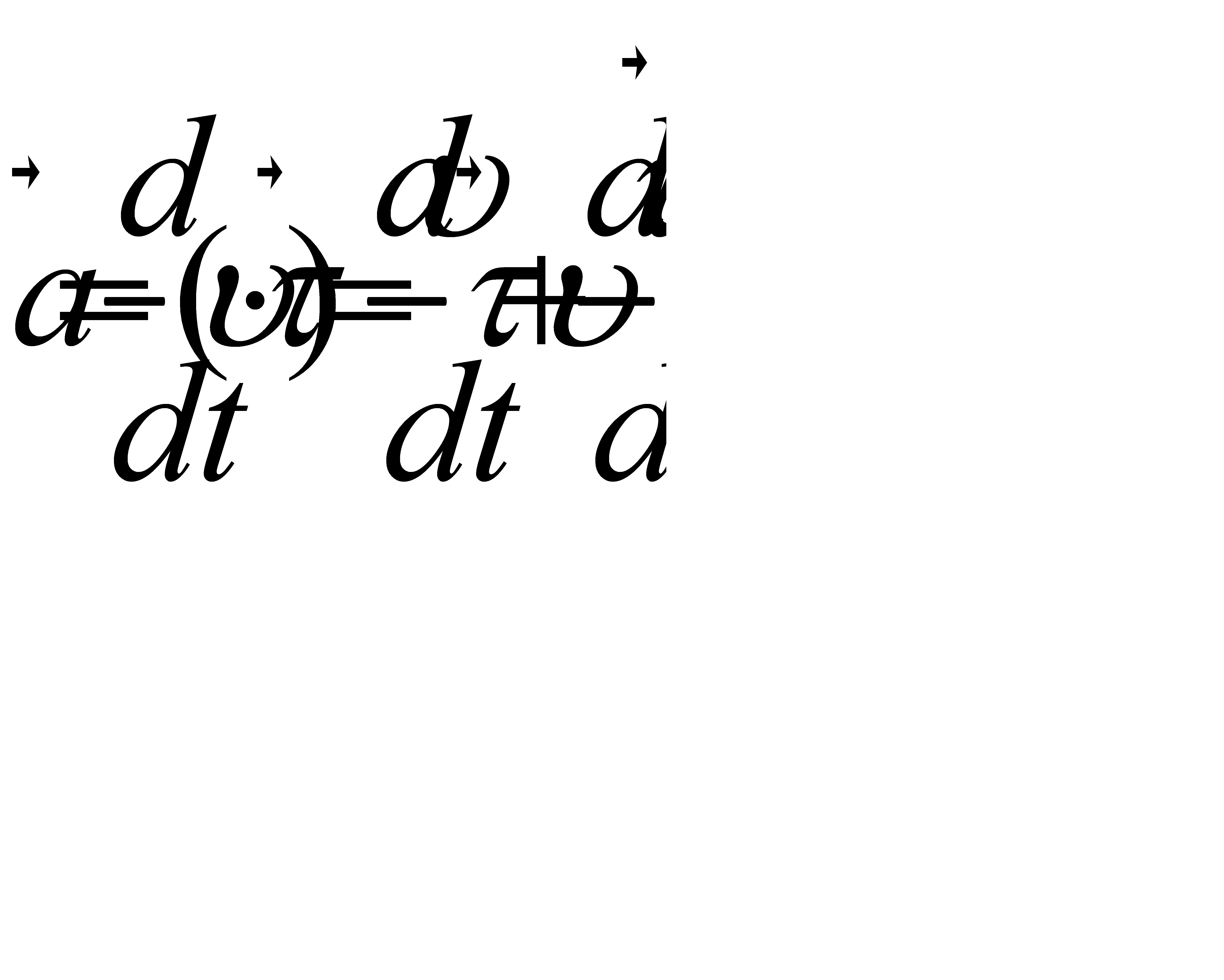 ;
; 
 +
+ 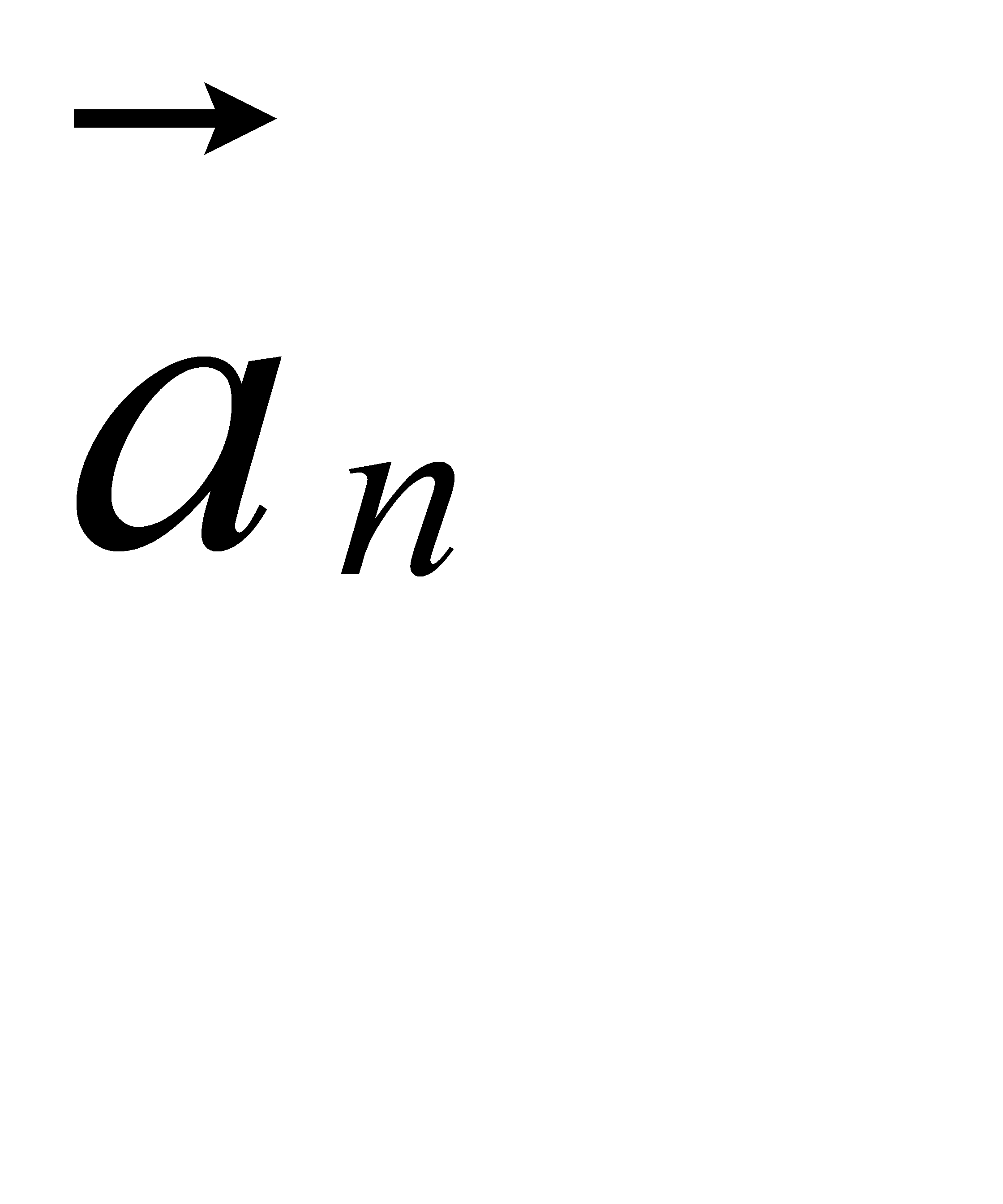

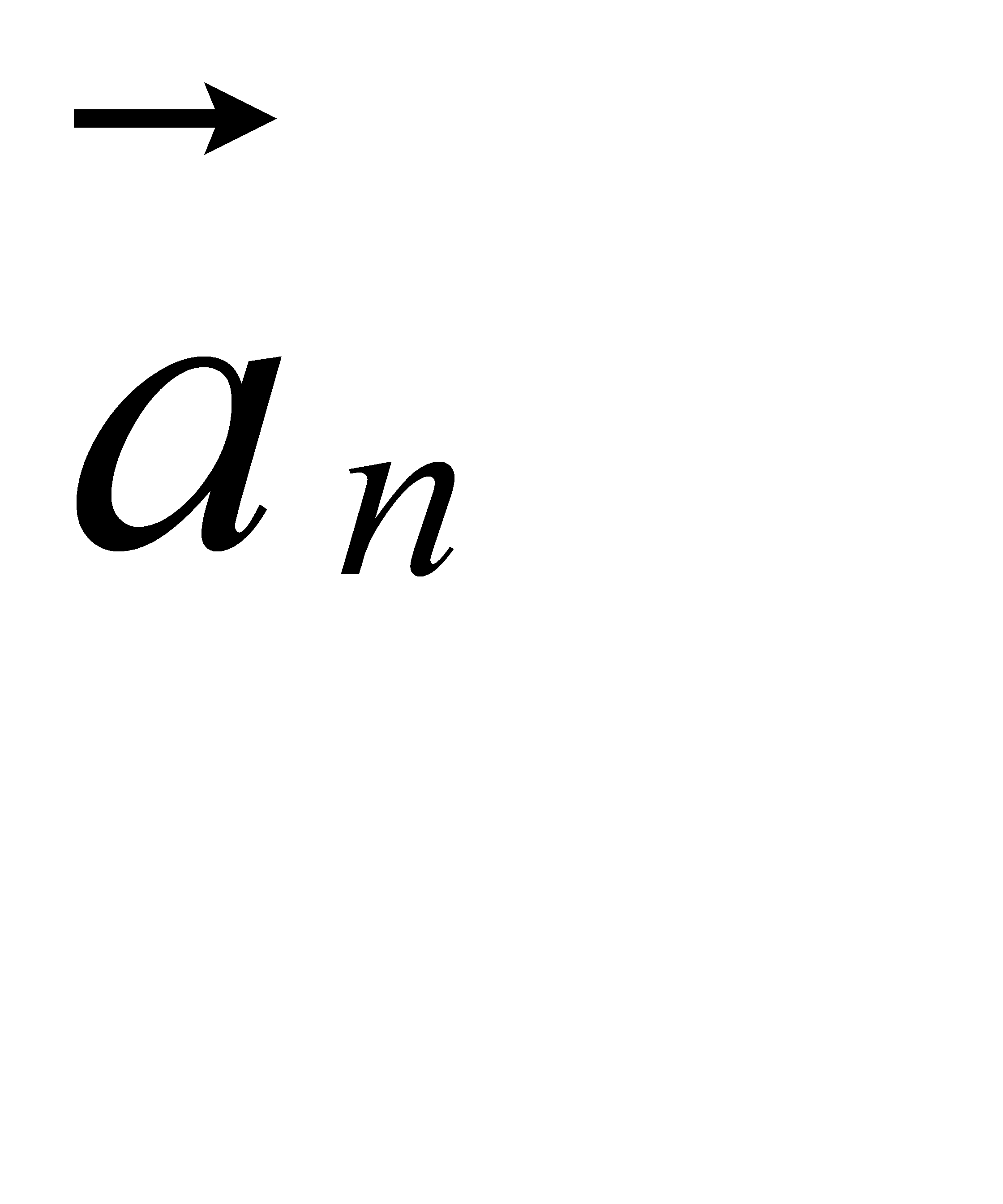
Тангенціальне прискорення  характеризує зміну швидкості за величиною і спрямоване по дотичній. Нормальне , або доцентрове – характеризує зміну швидкості за напрямком і спрямоване вздовж радіуса кривизни траекторії до центра. Повне прискорення за модулем дорівнює :
характеризує зміну швидкості за величиною і спрямоване по дотичній. Нормальне , або доцентрове – характеризує зміну швидкості за напрямком і спрямоване вздовж радіуса кривизни траекторії до центра. Повне прискорення за модулем дорівнює :

Знайдемо  - ? Розглянемо рух матеріальної точки по колу радіуса R
- ? Розглянемо рух матеріальної точки по колу радіуса R

|
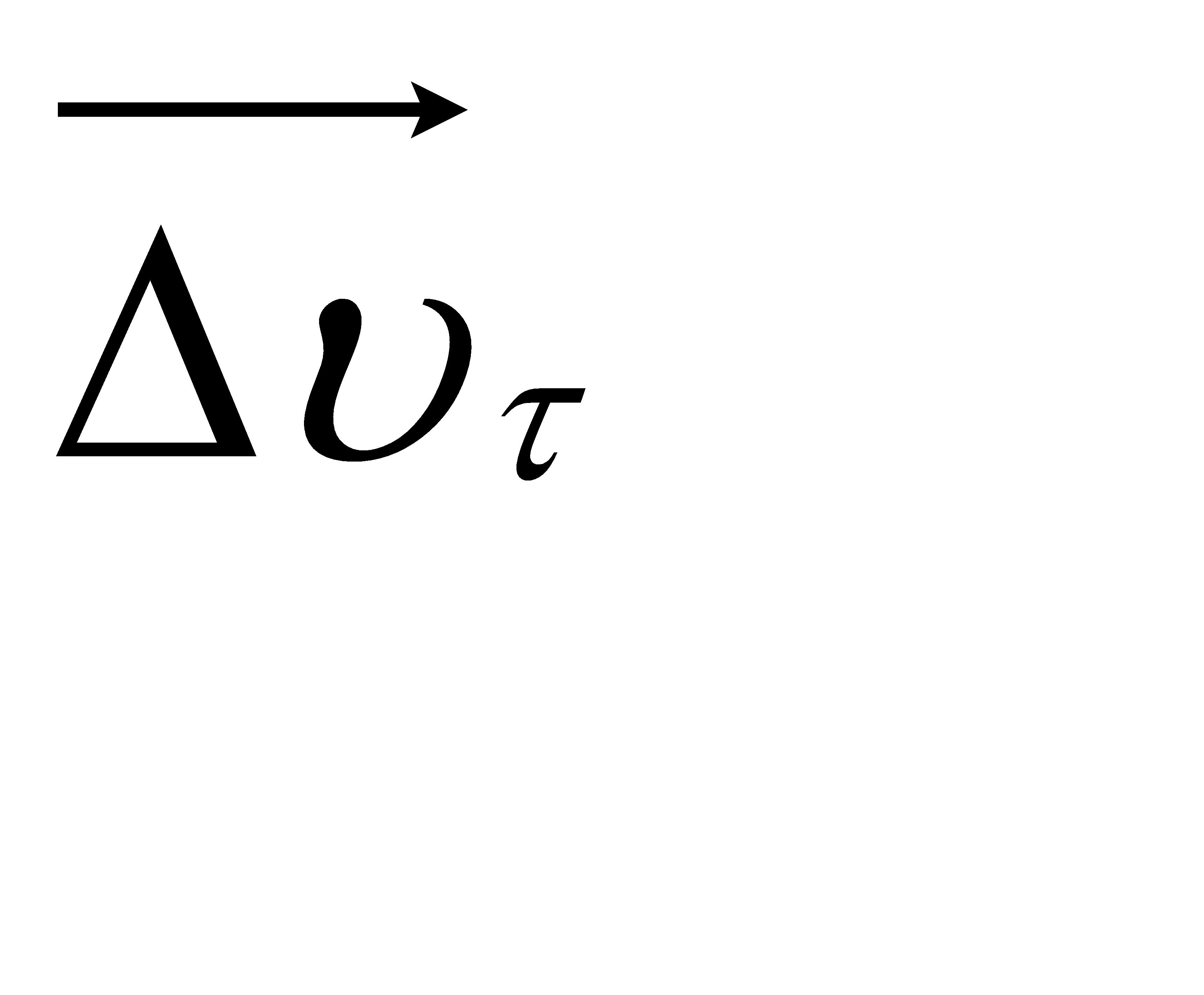
|
| Із подібності трикутників АОВ та ЕАD : |
| А |
| D |
| В |
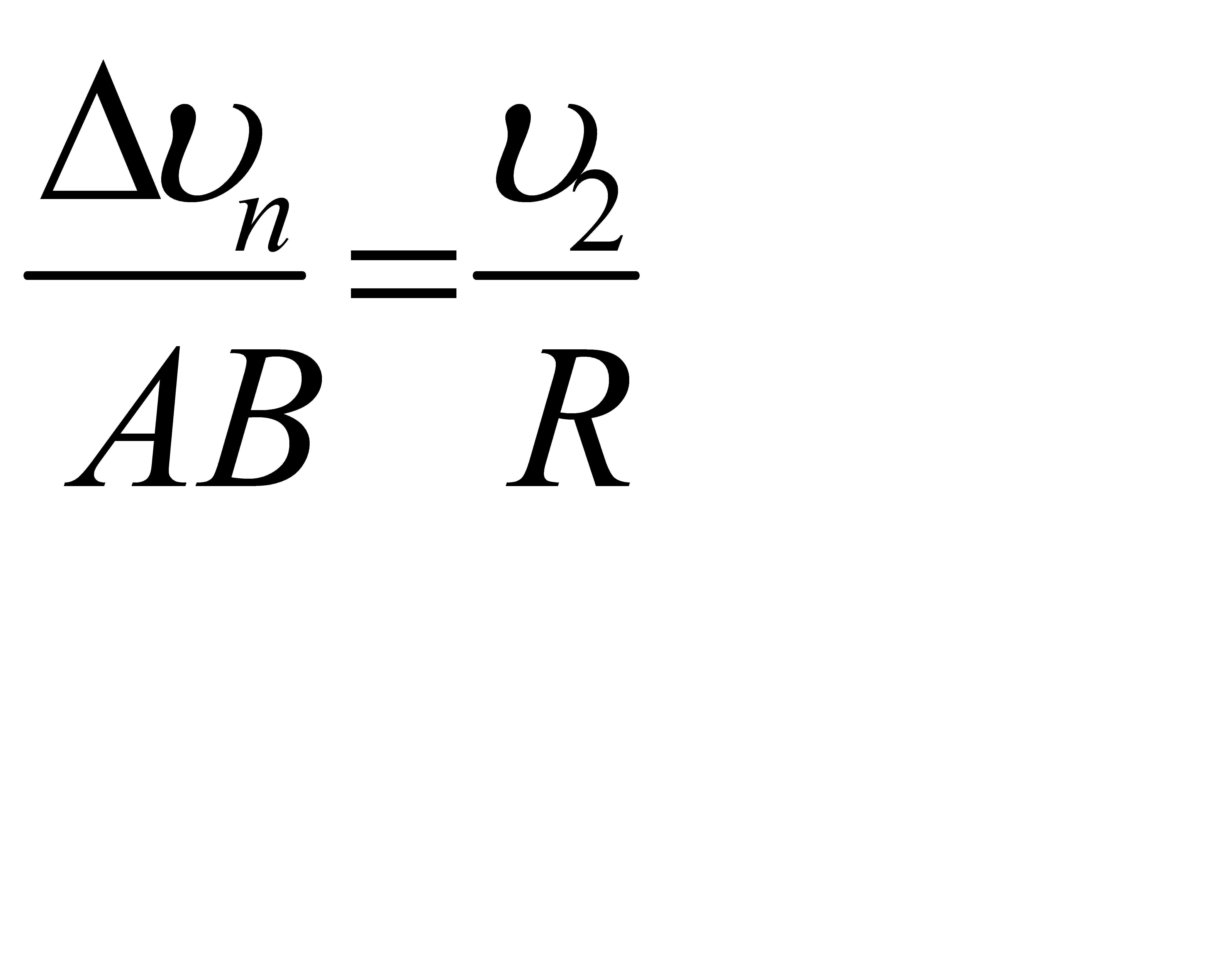 . .
|
|
R
E
| O |
Але АВ = 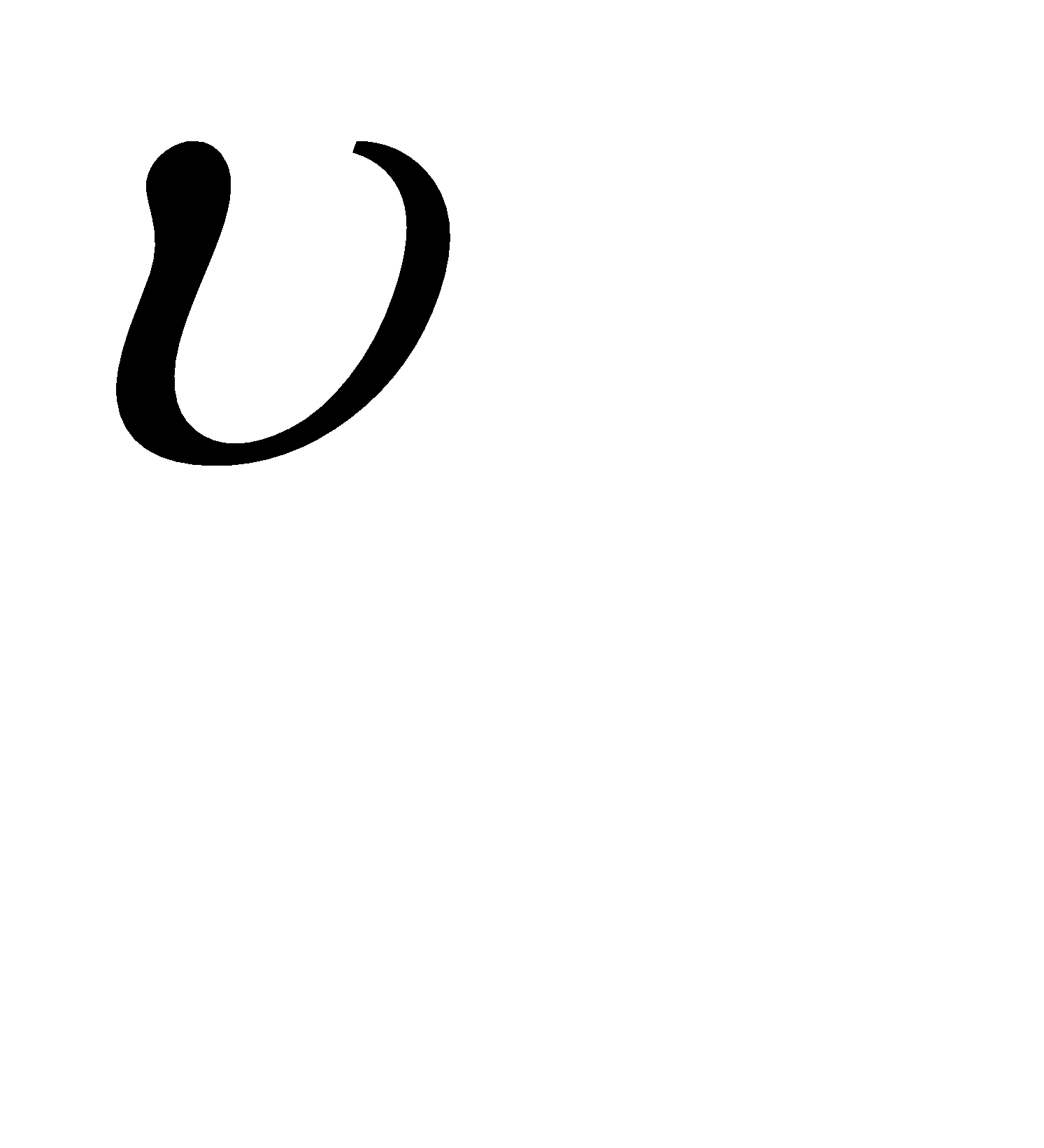 1 Δt , тоді
1 Δt , тоді
 при ,
при , 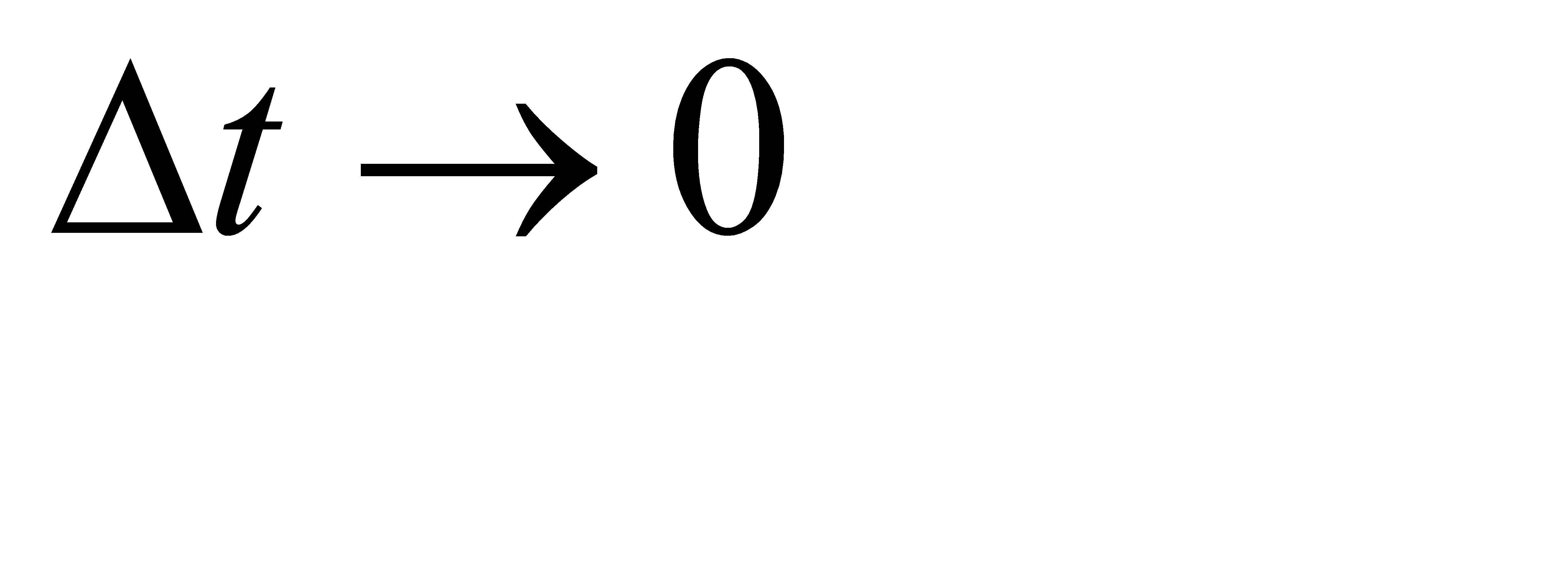 ,
,
При кут EAD 0 ,а кут ADE 90o , тому

. 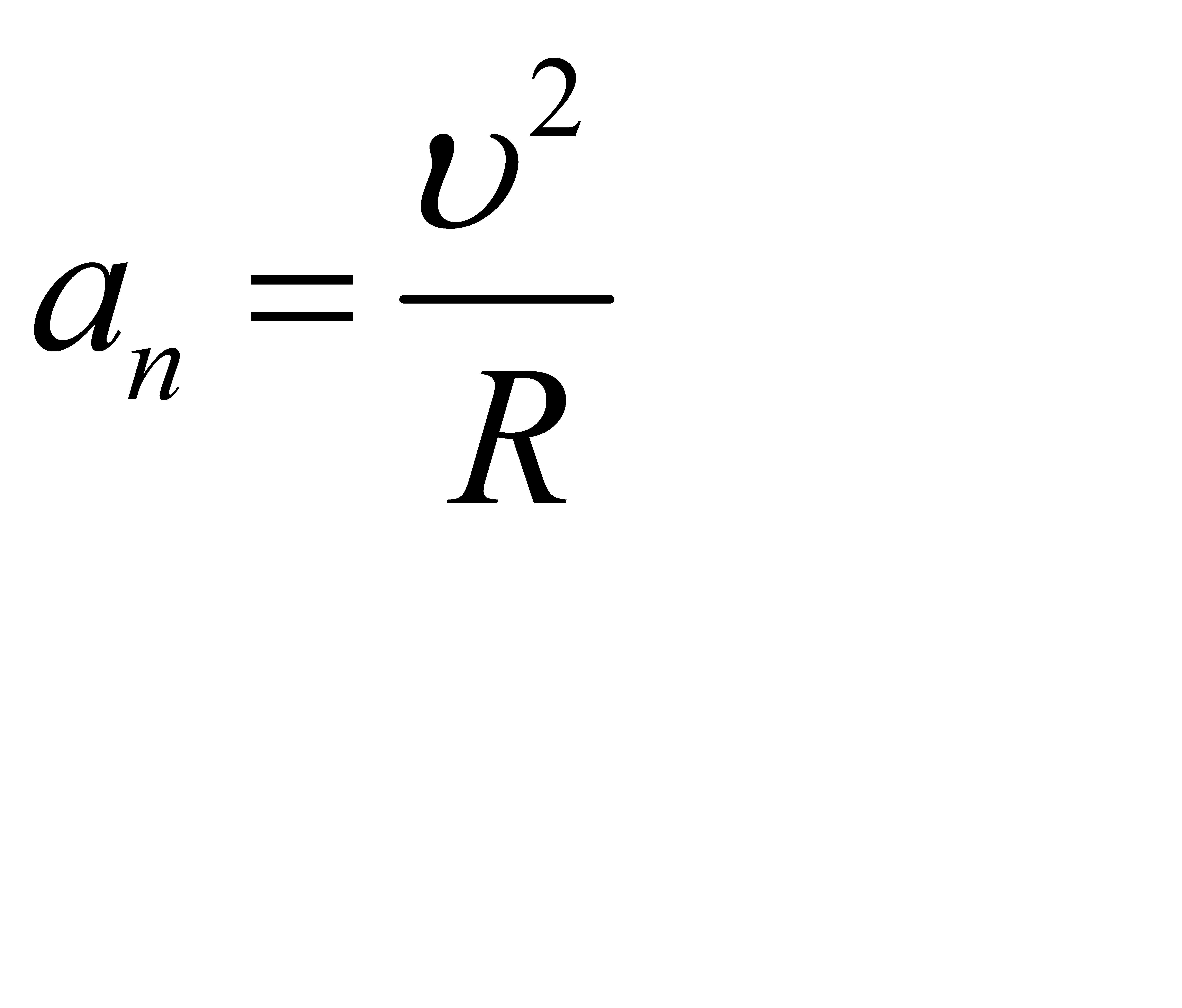
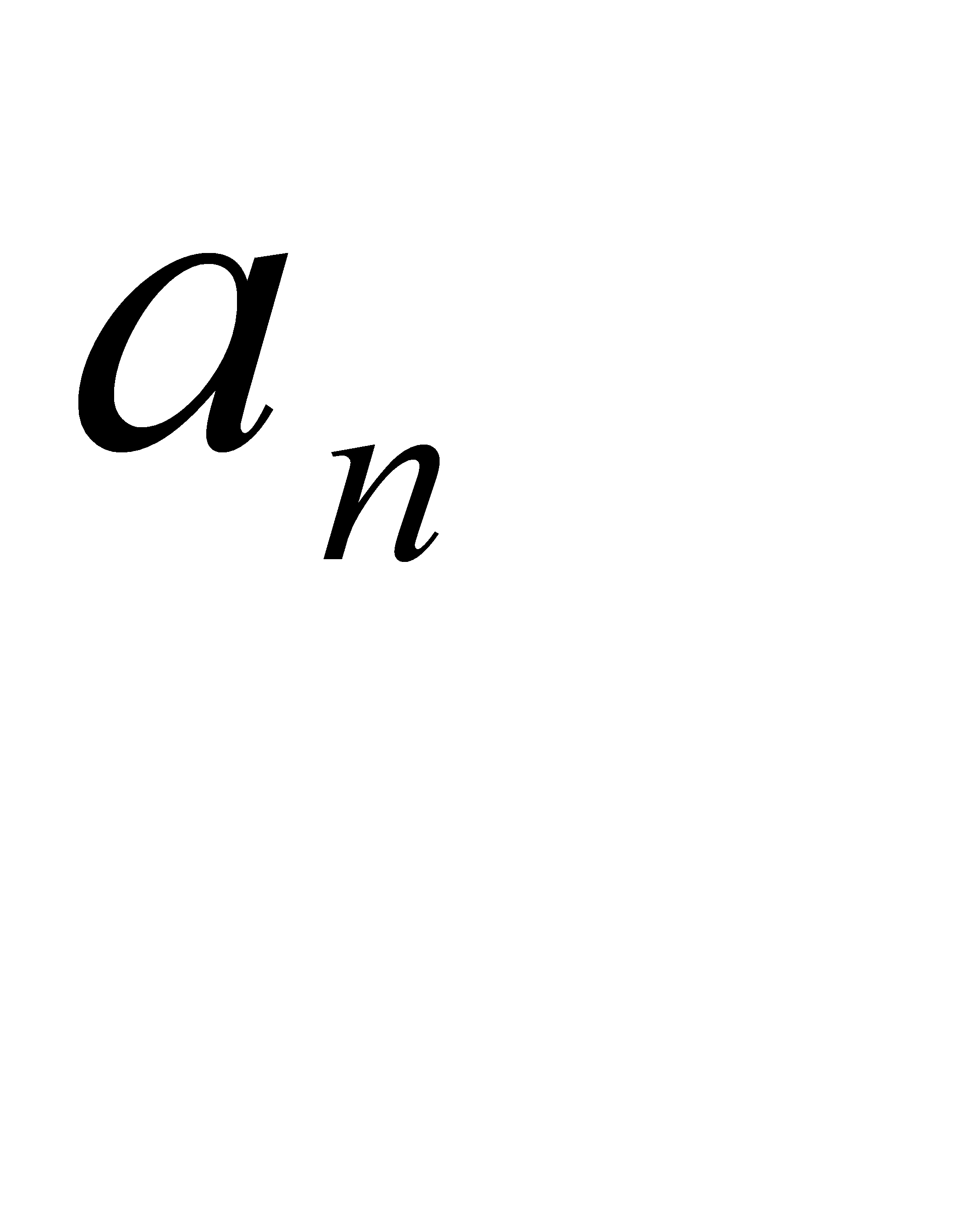
У зв’язку з введенням 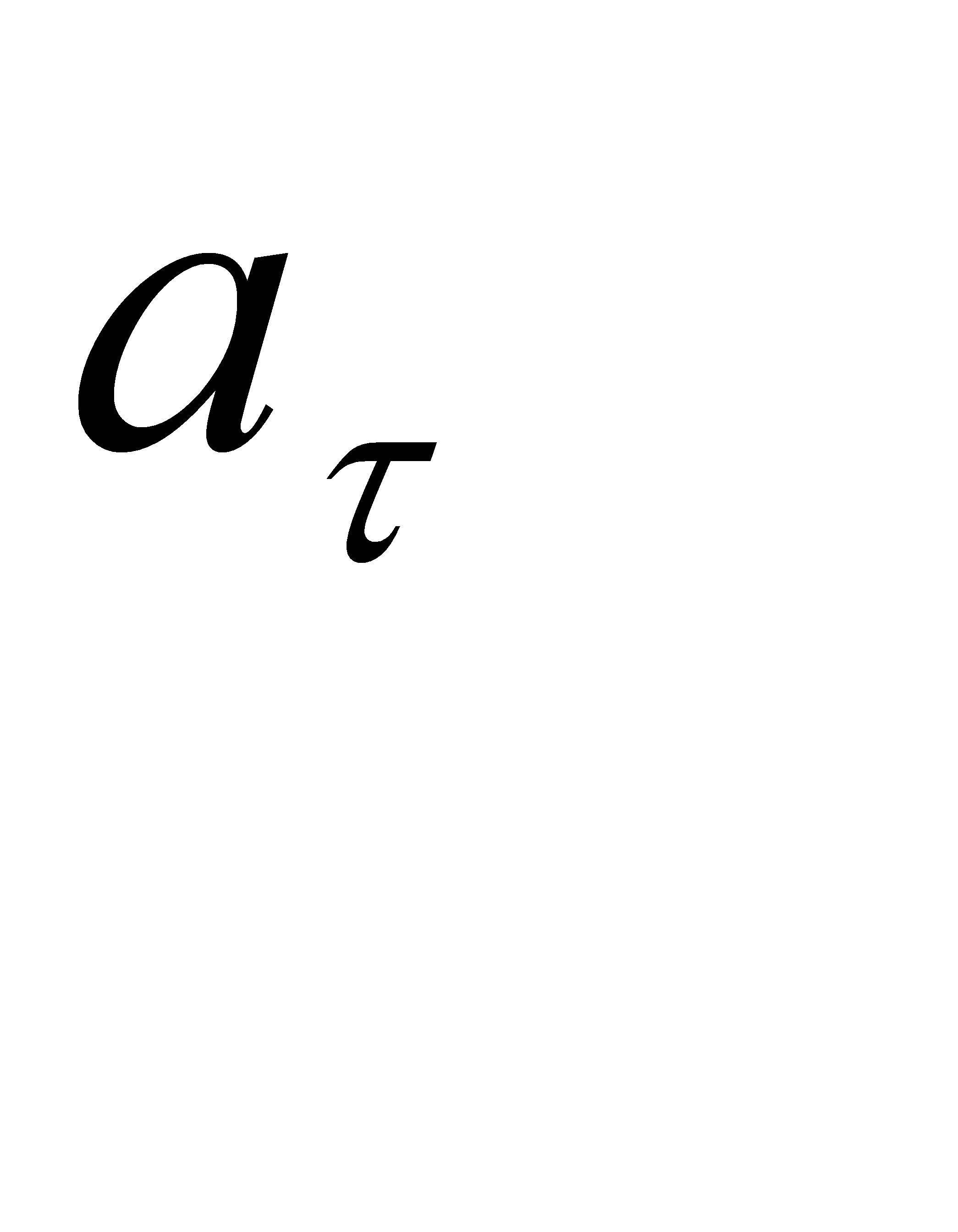 та
та 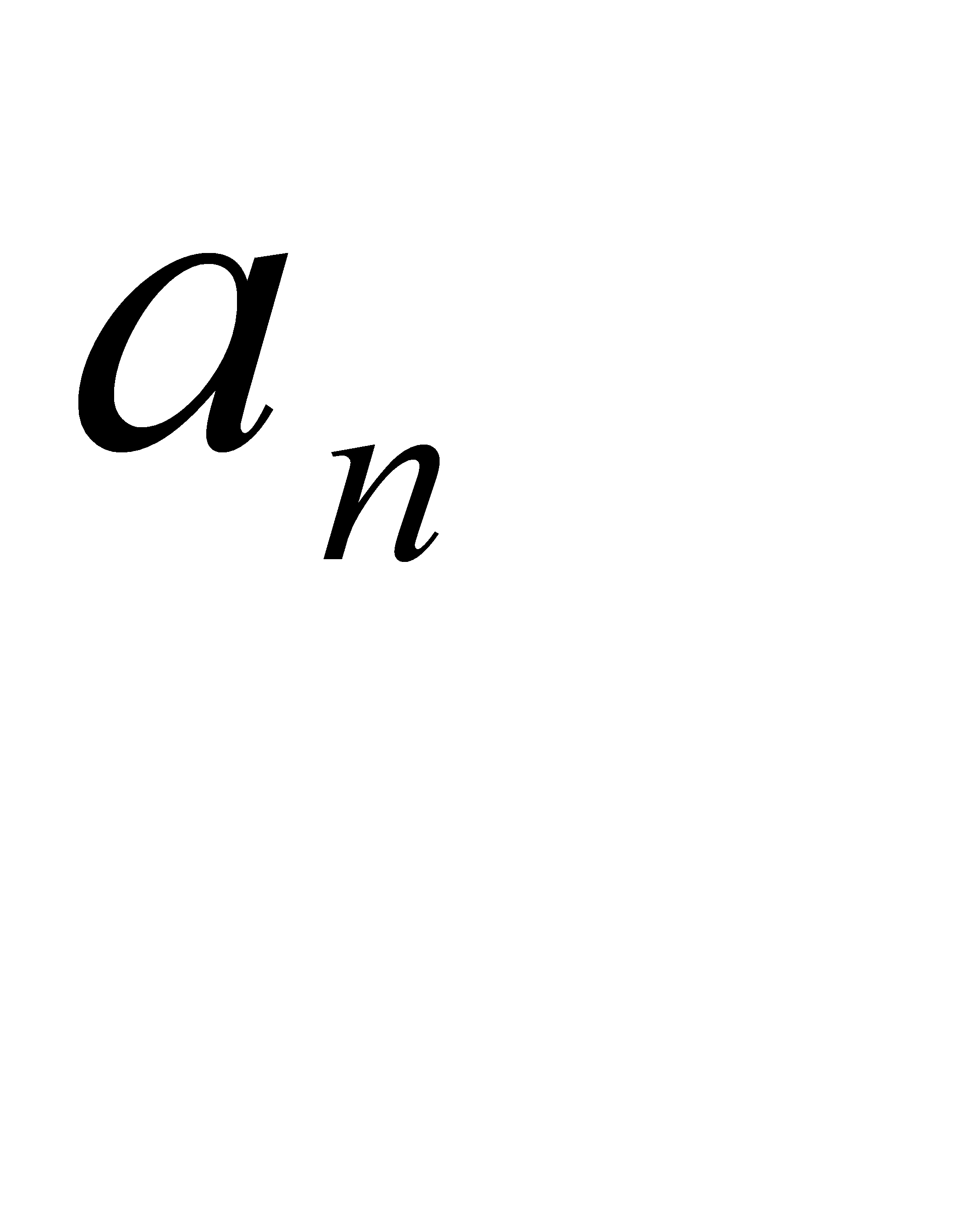 рух можна класифікувати наступним чином :
рух можна класифікувати наступним чином :
1. 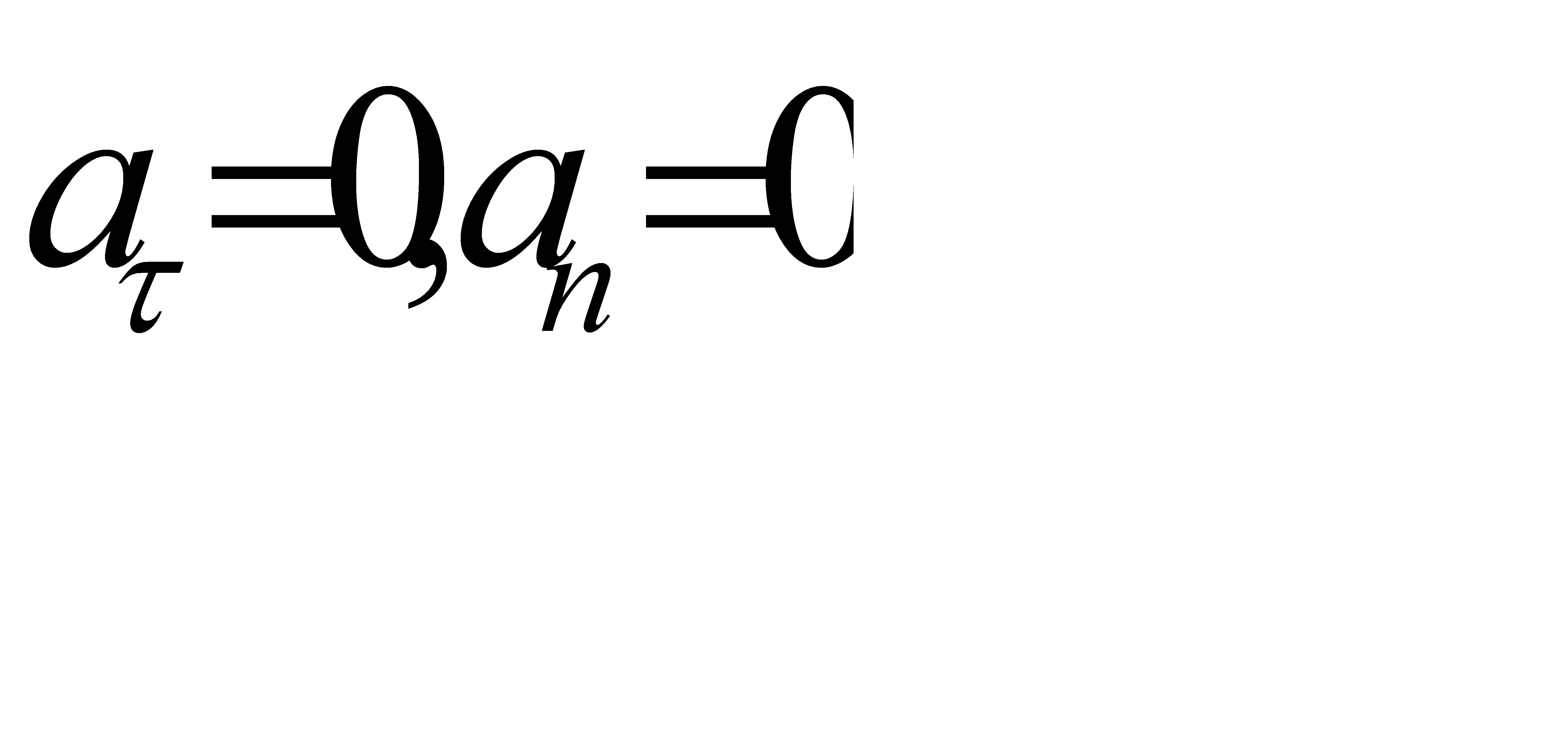 - рух прямолінійний та рівномірний ;
- рух прямолінійний та рівномірний ;
2. 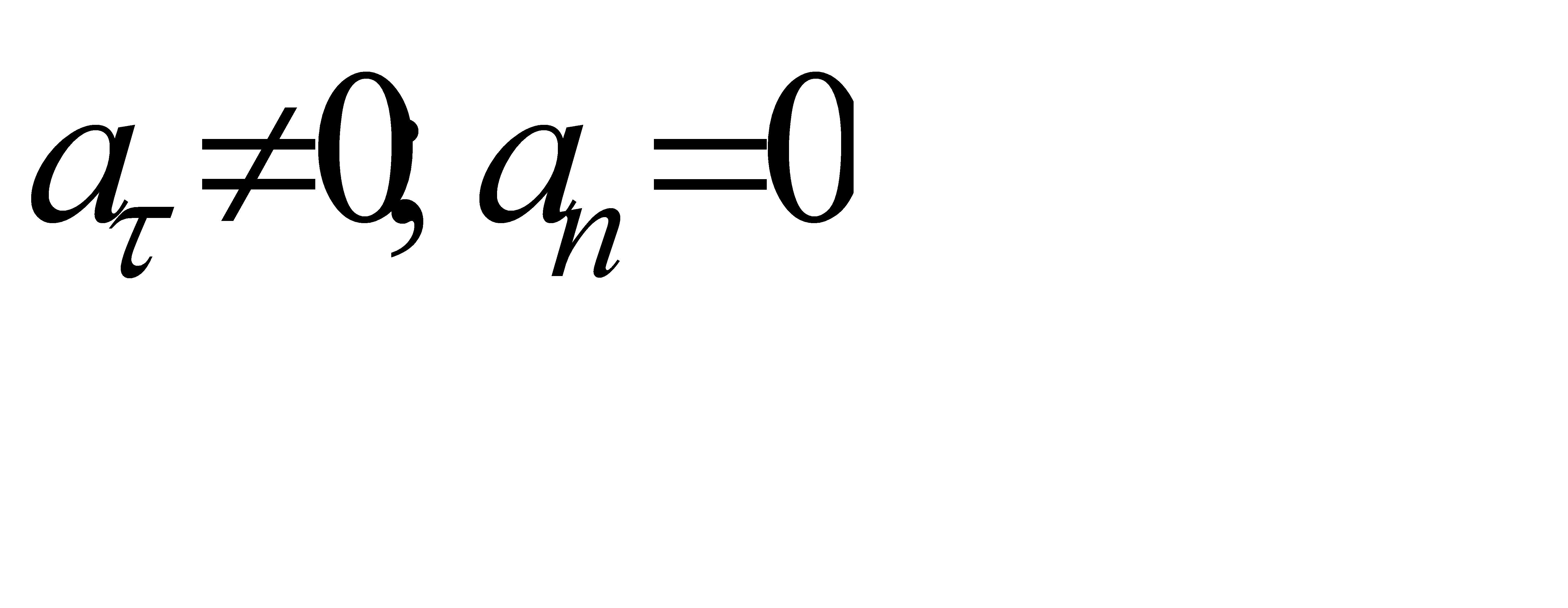 - рух прямолінійний , рівнозмінний ;
- рух прямолінійний , рівнозмінний ;
Для такого руху : 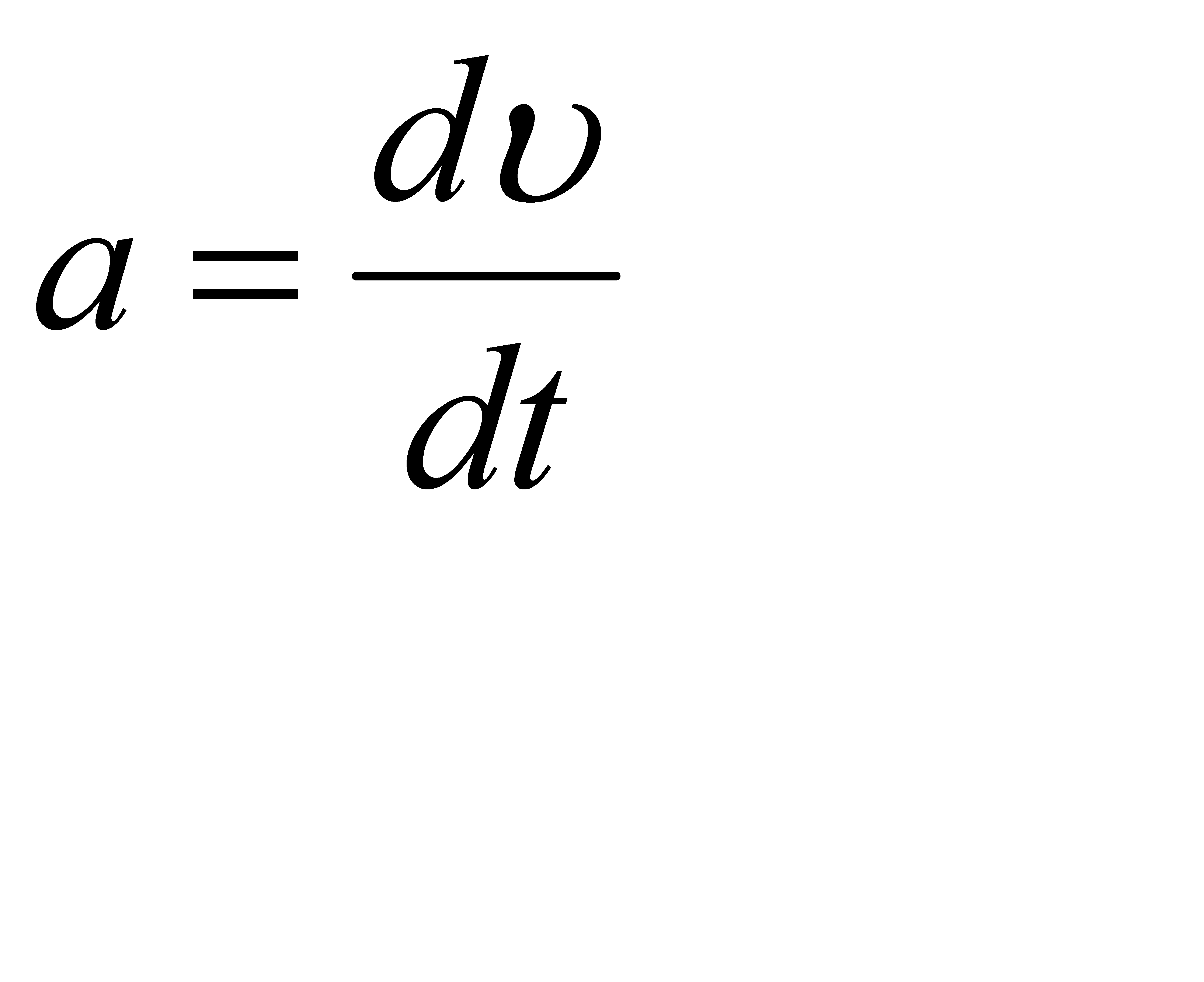 ;
; 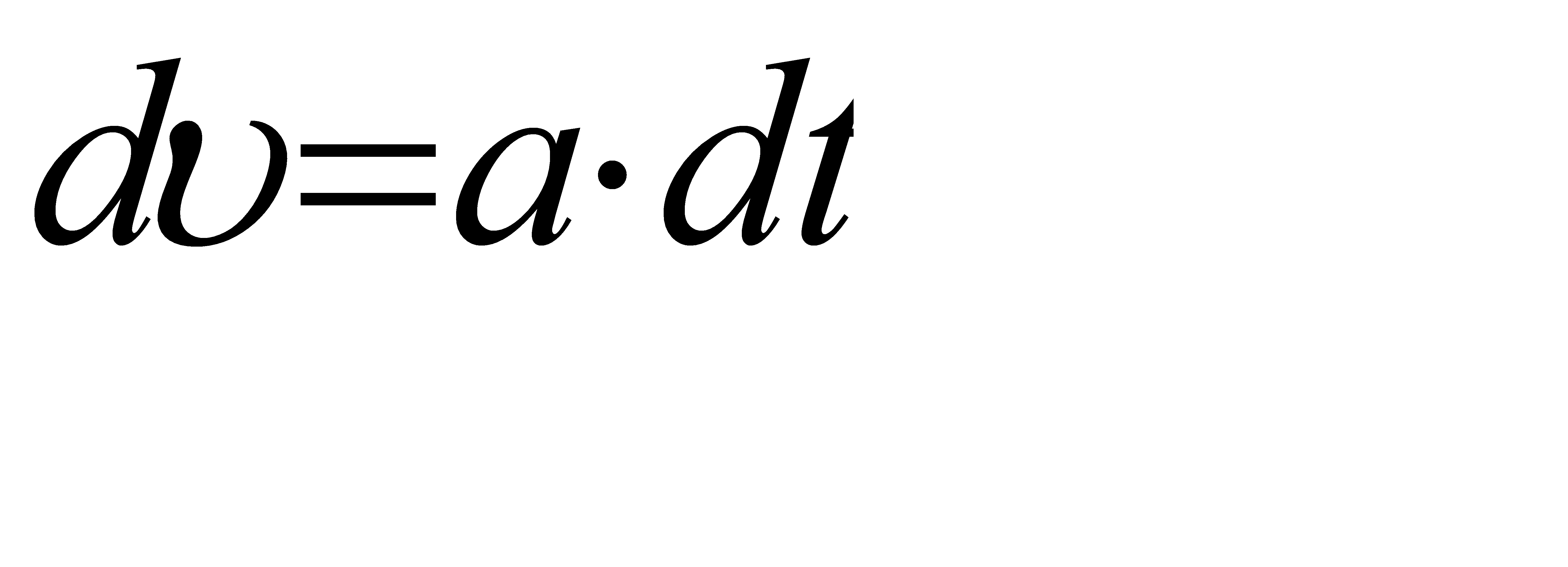 .
.
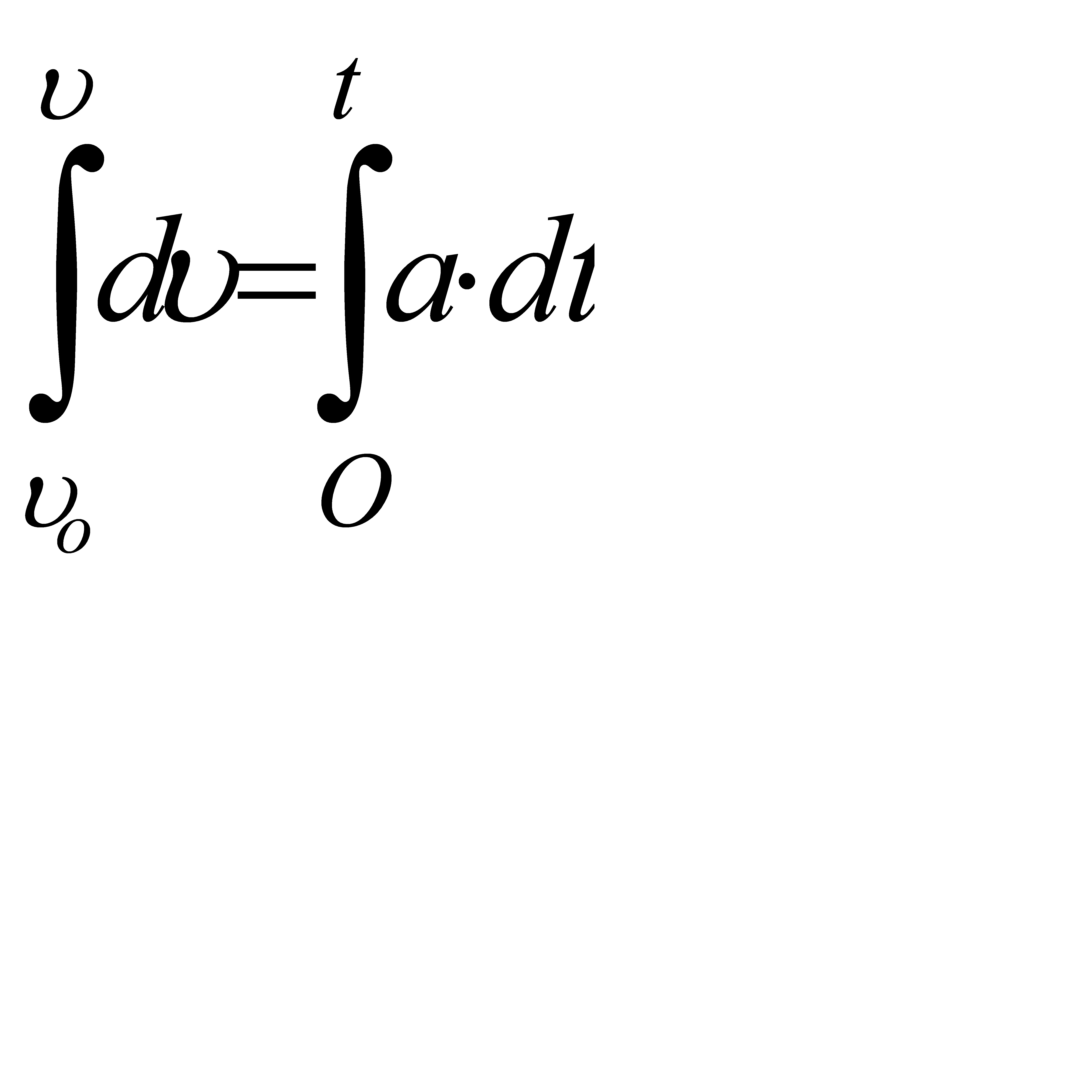 ;
; 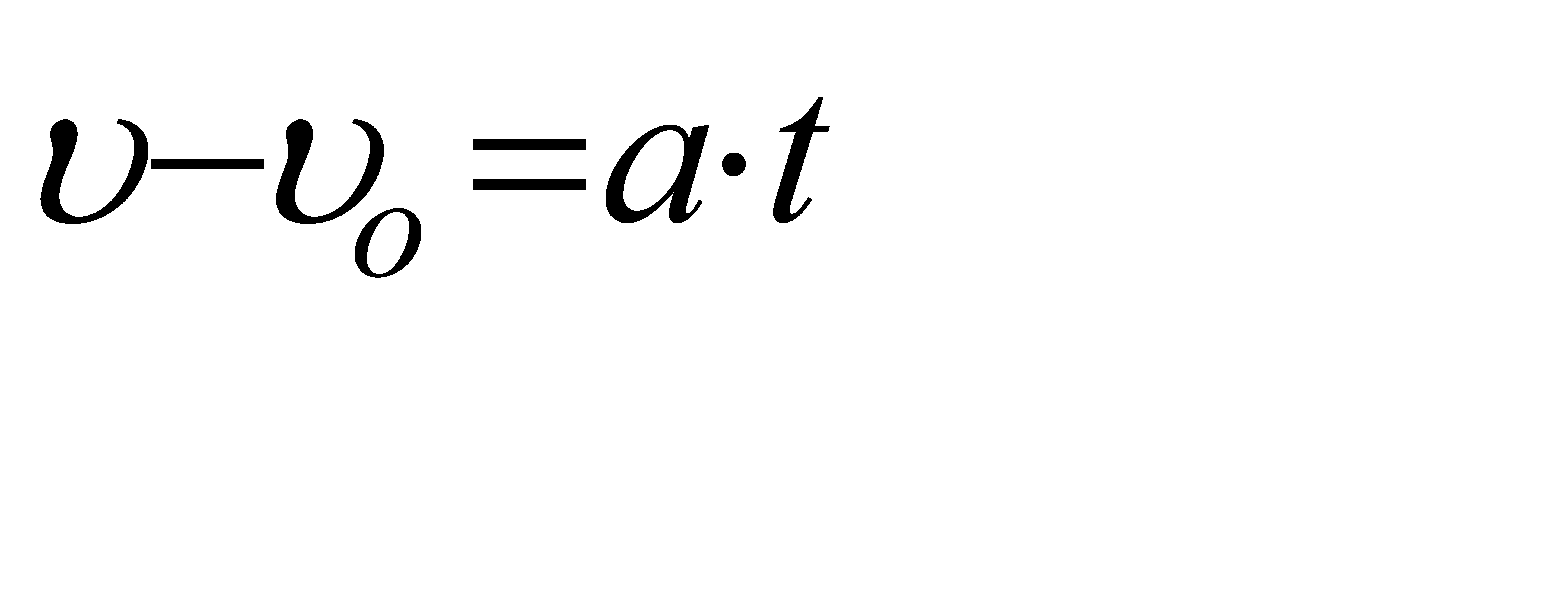 ;
;  .
.
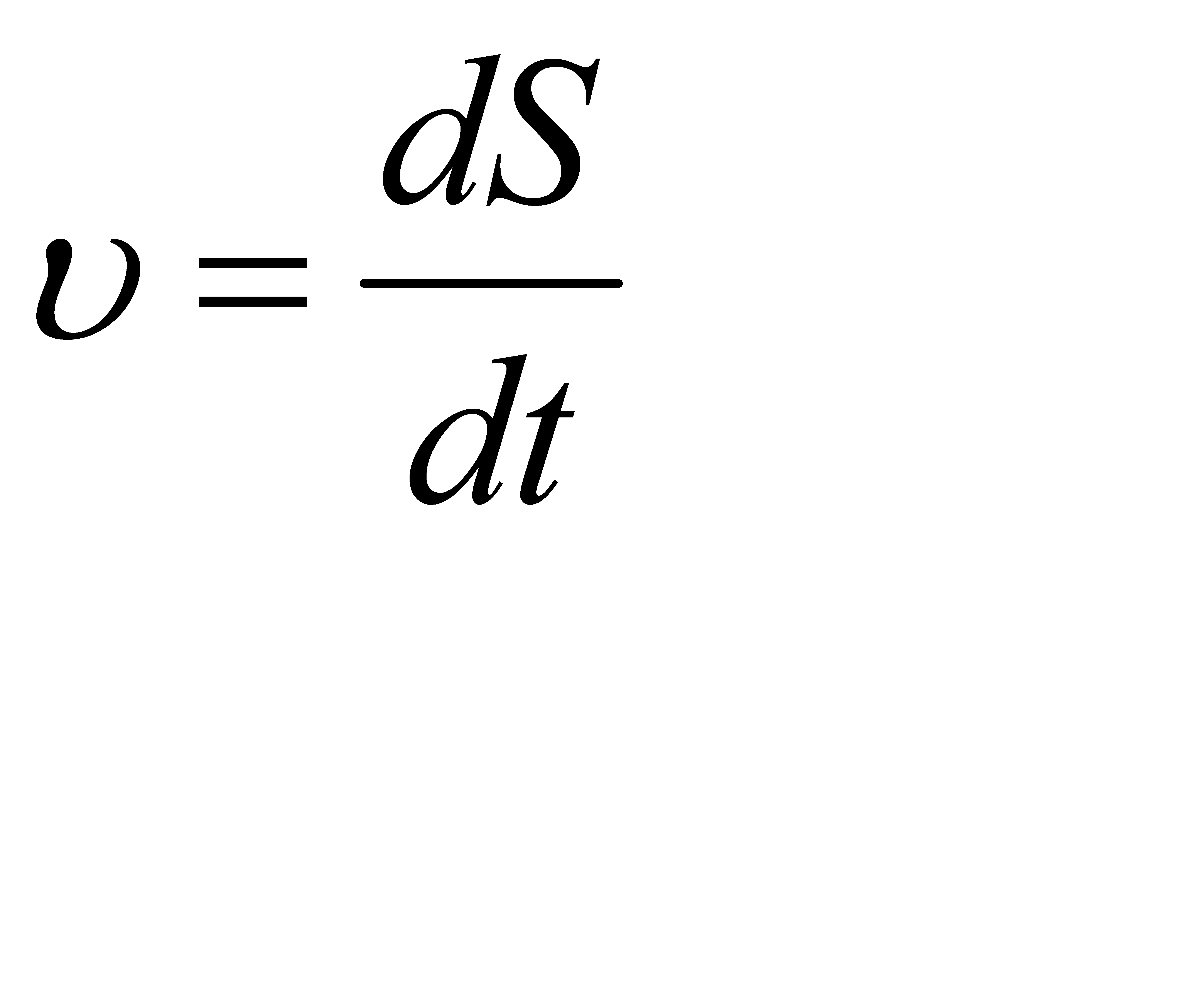 ;
; 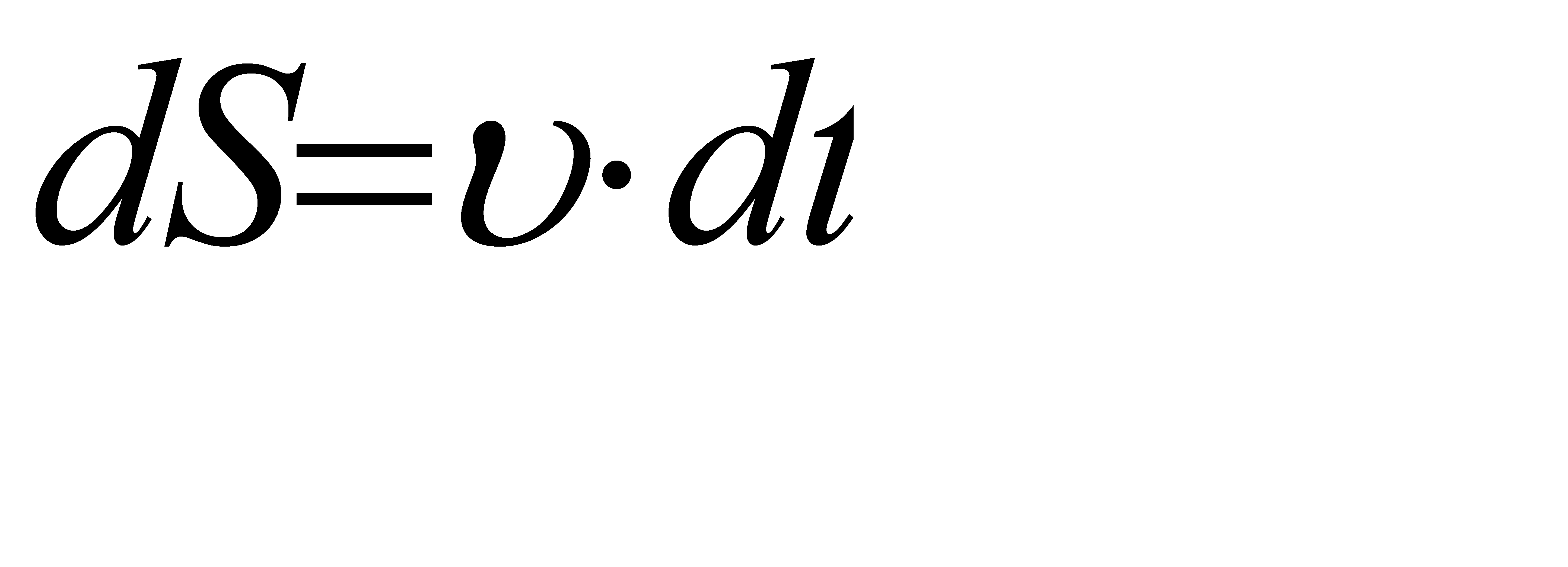 ;
; 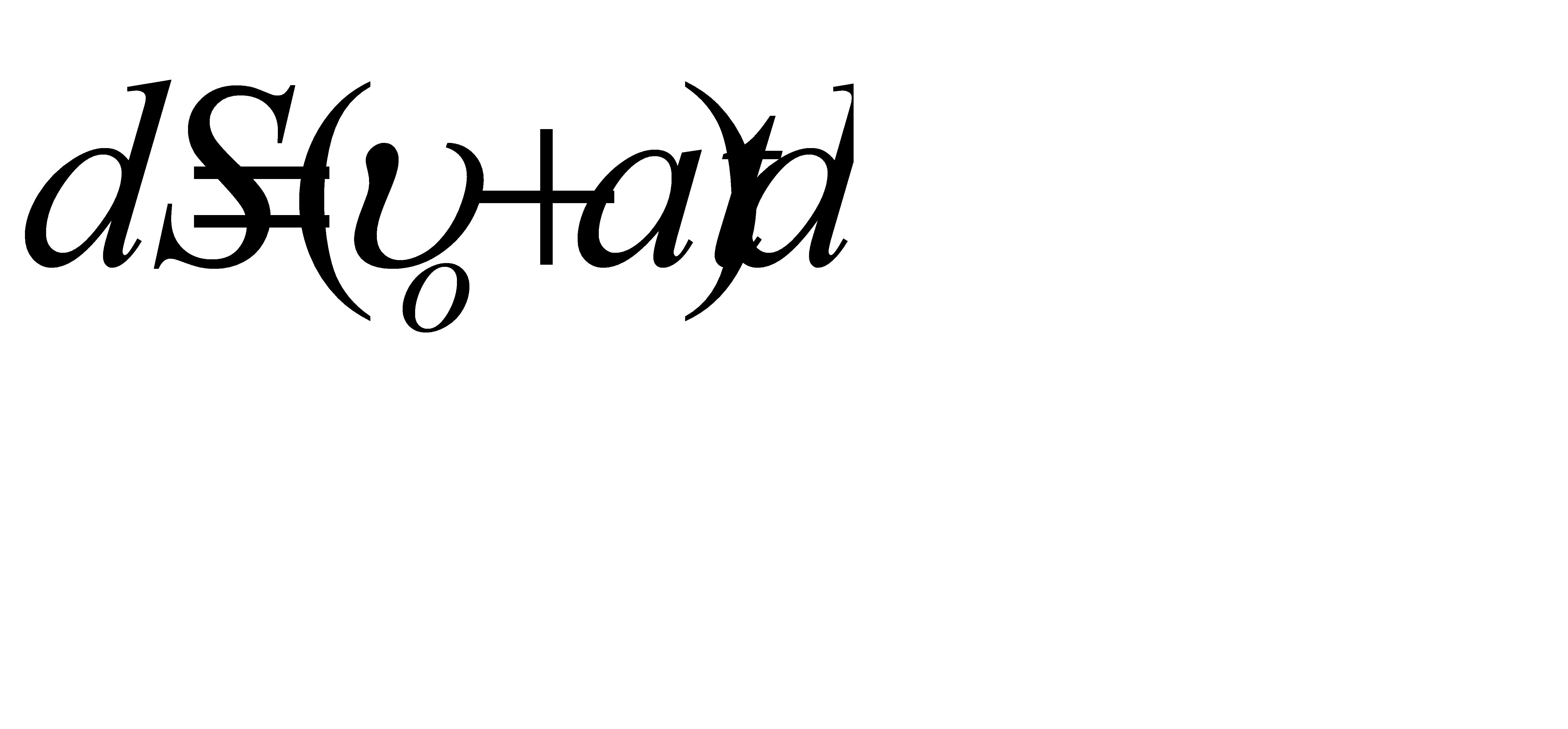 .
.
 ;
; 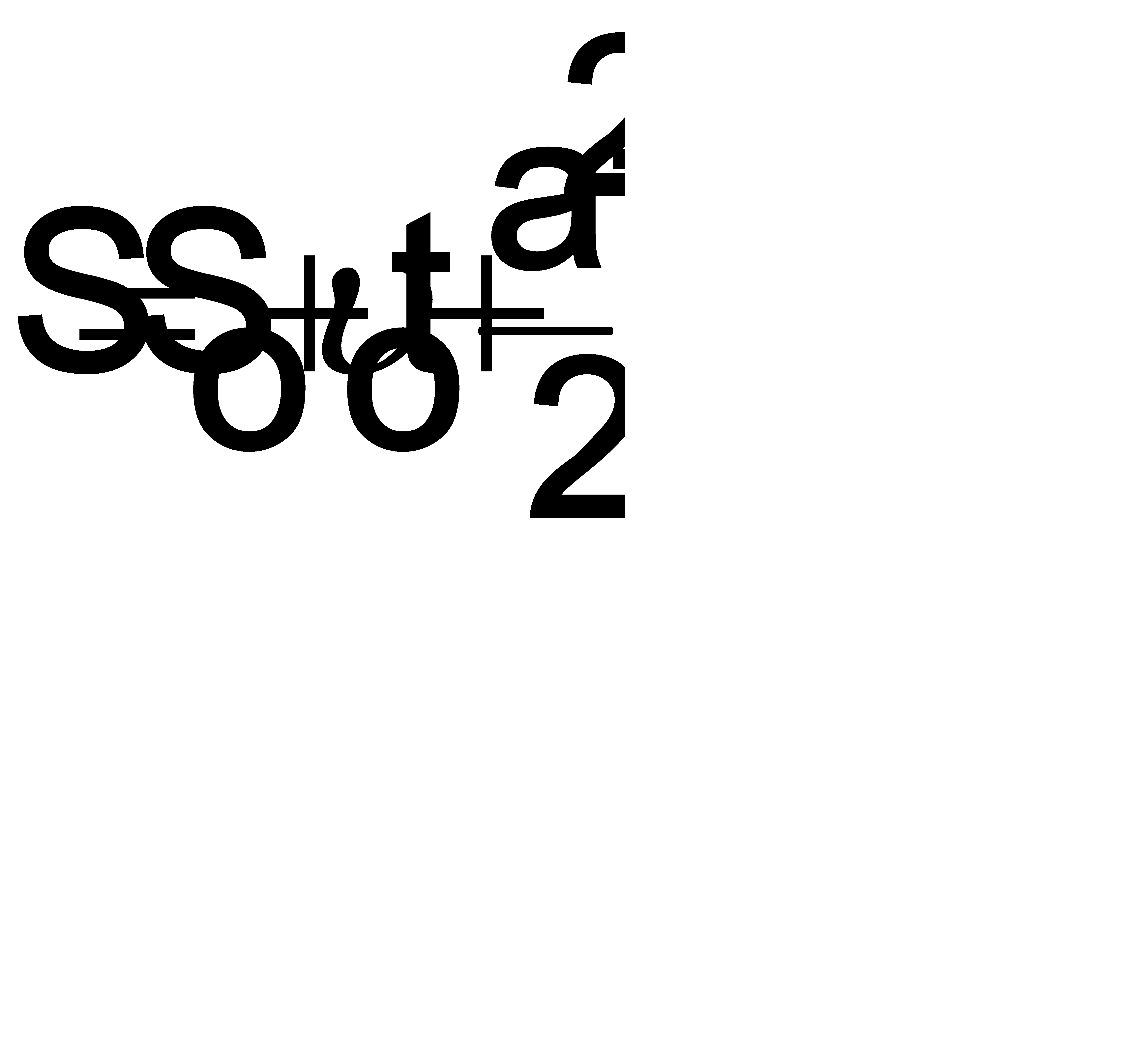 .
.
Лекція №2
2. Основи кінематики обертального руху
При обертальному русі твердого тіла навколо нерухомої осі всі його точки (крім тих , що лежать на осі) описують кола.
 0¢
0¢
напівплощина
Положення тіла, що обертається навколо своєї осі , повністю задається значенням кута 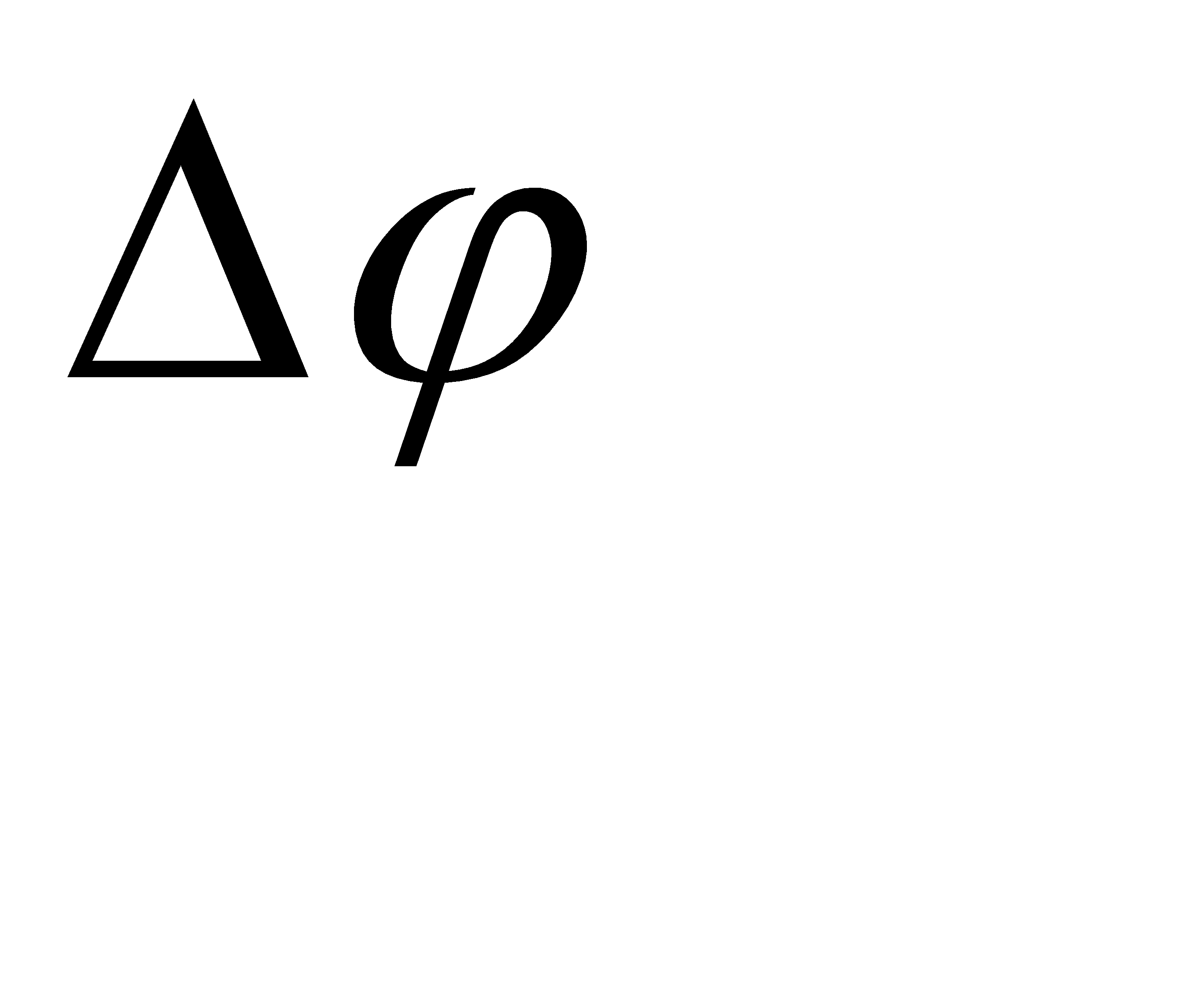 повороту із деякого початкового моменту. повороту із деякого початкового моменту.
|
ω
Δϕ
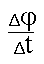
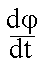
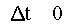 Кутовою швидкістю називається величина ω = lim = ;
Кутовою швидкістю називається величина ω = lim = ;
Кутову швидкість доцільно визначити як осьовий вектор - ω ,
напрямок , якого визначається за правилом правого гвинта, іякий відкладається із будь-якої точки на осі.
z
Зв’язок між векторами та ω :
із рисунка слідує
| R |
 Зв’язок модулів :
u = ωR
[ ω ] = 1 рад/с - одиниця виміру ;
[ω] = T-1
Зв’язок модулів :
u = ωR
[ ω ] = 1 рад/с - одиниця виміру ;
[ω] = T-1
|
| М |
ω

|
| O |
x
Для характеристики зміни кутової швидкості при нерівномірному русі служить вектор e – кутового прискорення.
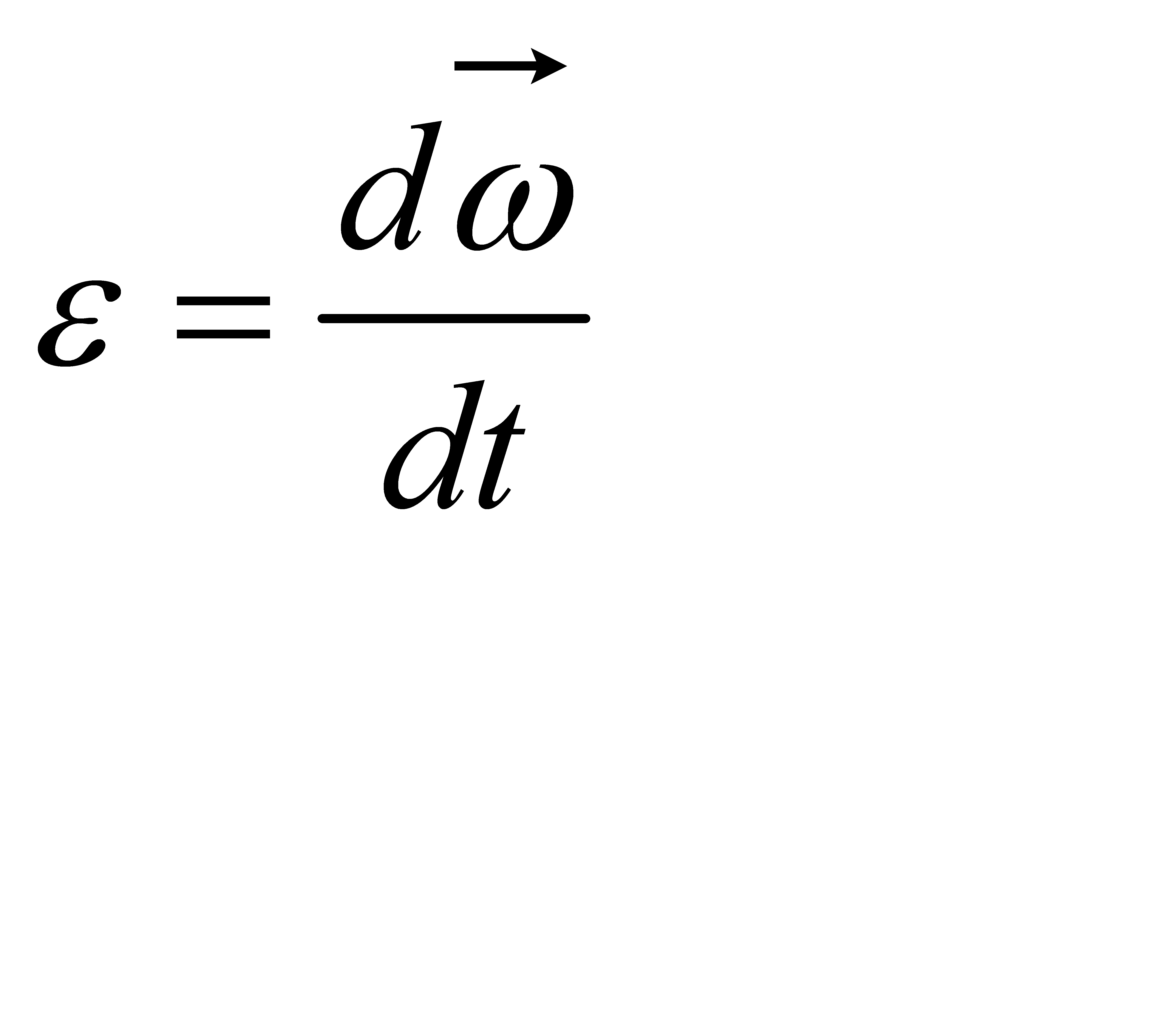 .
.
Вектор e завжди спрямований вздовж осі обертання і відкладається з будьякої точки на осі.
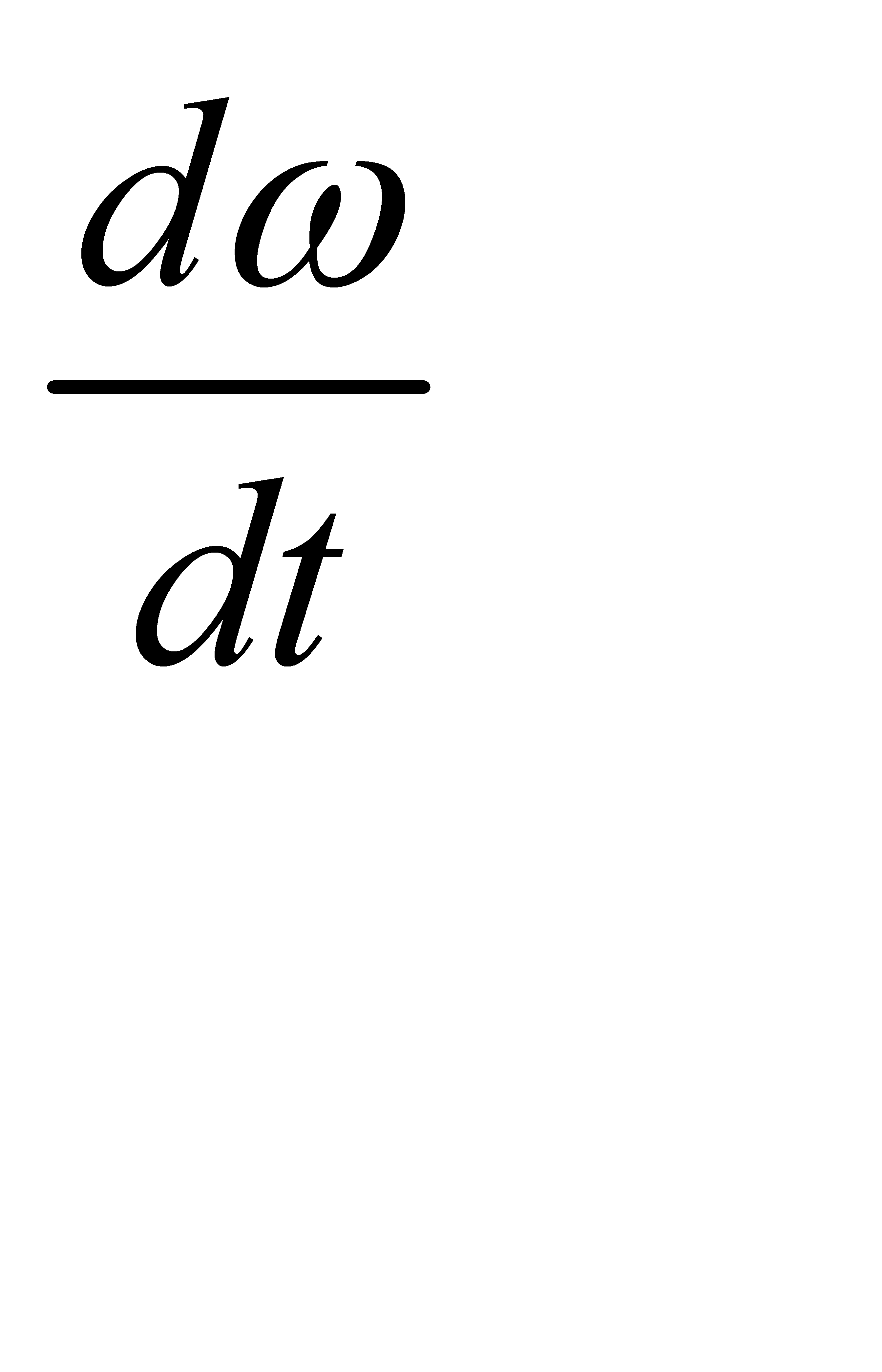
↑↑   > 0 ; > 0 ;
|
ω
 oL dzfeJhaxHcXbNvw9y4keRzOaeVNtZj+IE07JxaAhWygQGNpoXeg0fO7e7gsQiUywZogBNfxggk19 fVWZ0sZzaPC0pU5wSUil0dATjaWUqe3Rm7SIIwb2DnHyhlhOnbSTOXO5H+SDUivpjQu80JsRX3ps v7dHr6Fwq7smn94b9ZFT576KnaP5Vevbm/l5DYJwpv8w/OEzOtTMtI/HYJMYWOcFo5OGR7UEwYGl yjIQe3ZU9gSyruTlhfoXAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAA AAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAA CwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEA+8JeTbQCAADEBQAA DgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAjL6inN0AAAAK AQAADwAAAAAAAAAAAAAAAAAOBQAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAABgGAAAA AA== " strokeweight=".26mm"> e
oL dzfeJhaxHcXbNvw9y4keRzOaeVNtZj+IE07JxaAhWygQGNpoXeg0fO7e7gsQiUywZogBNfxggk19 fVWZ0sZzaPC0pU5wSUil0dATjaWUqe3Rm7SIIwb2DnHyhlhOnbSTOXO5H+SDUivpjQu80JsRX3ps v7dHr6Fwq7smn94b9ZFT576KnaP5Vevbm/l5DYJwpv8w/OEzOtTMtI/HYJMYWOcFo5OGR7UEwYGl yjIQe3ZU9gSyruTlhfoXAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAA AAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAA CwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEA+8JeTbQCAADEBQAA DgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAjL6inN0AAAAK AQAADwAAAAAAAAAAAAAAAAAOBQAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAABgGAAAA AA== " strokeweight=".26mm"> e
an u
at
| |

 ω
ω
аn
аt
Обертання тіла характеризується також періодом обертання Тта частотою обертання n.
Період обертання – це час, протягом якого тіло робить оберт навколо своєї осі.
Частота – це кількість обертів, які здійснює тідо за одиницю часу.
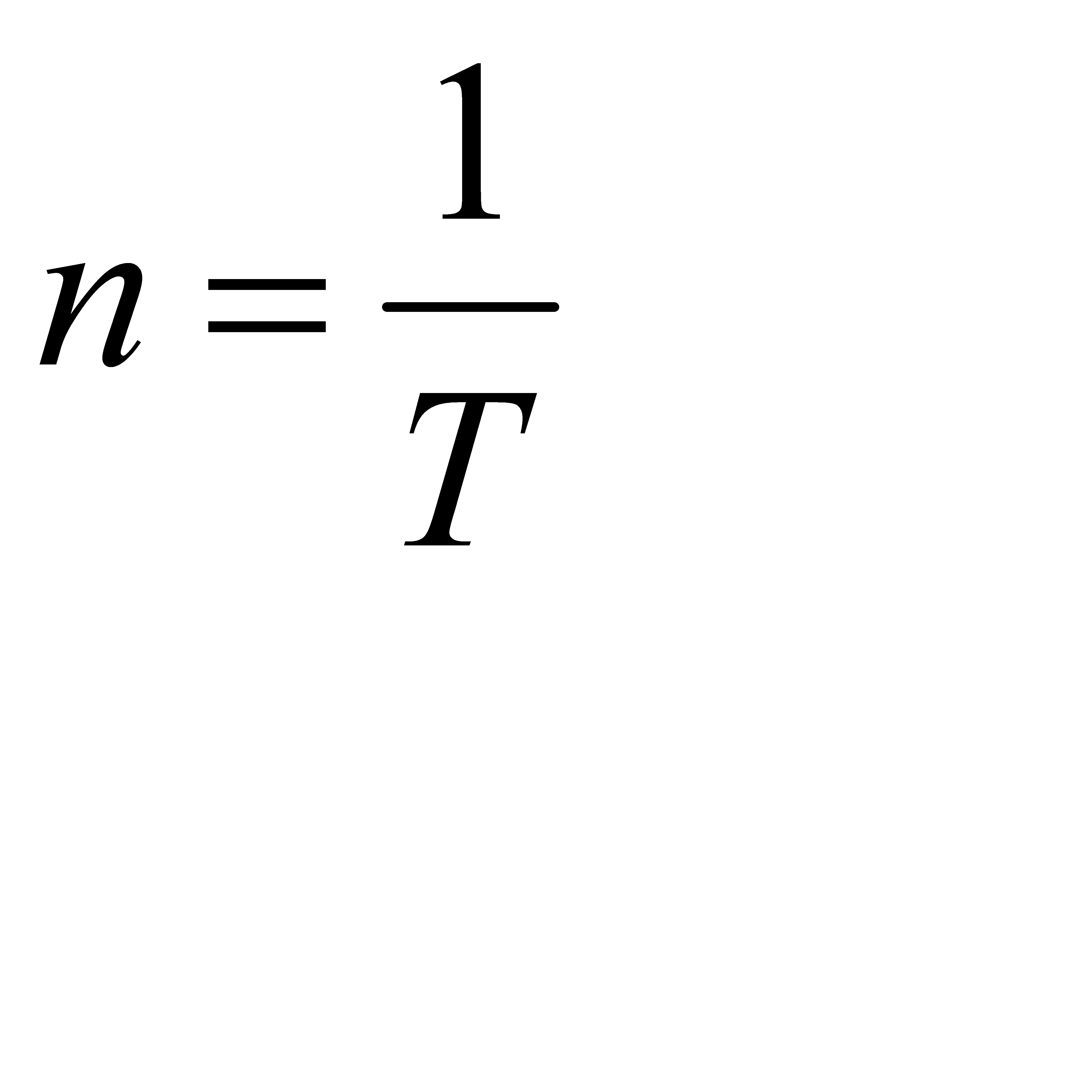 ;
; 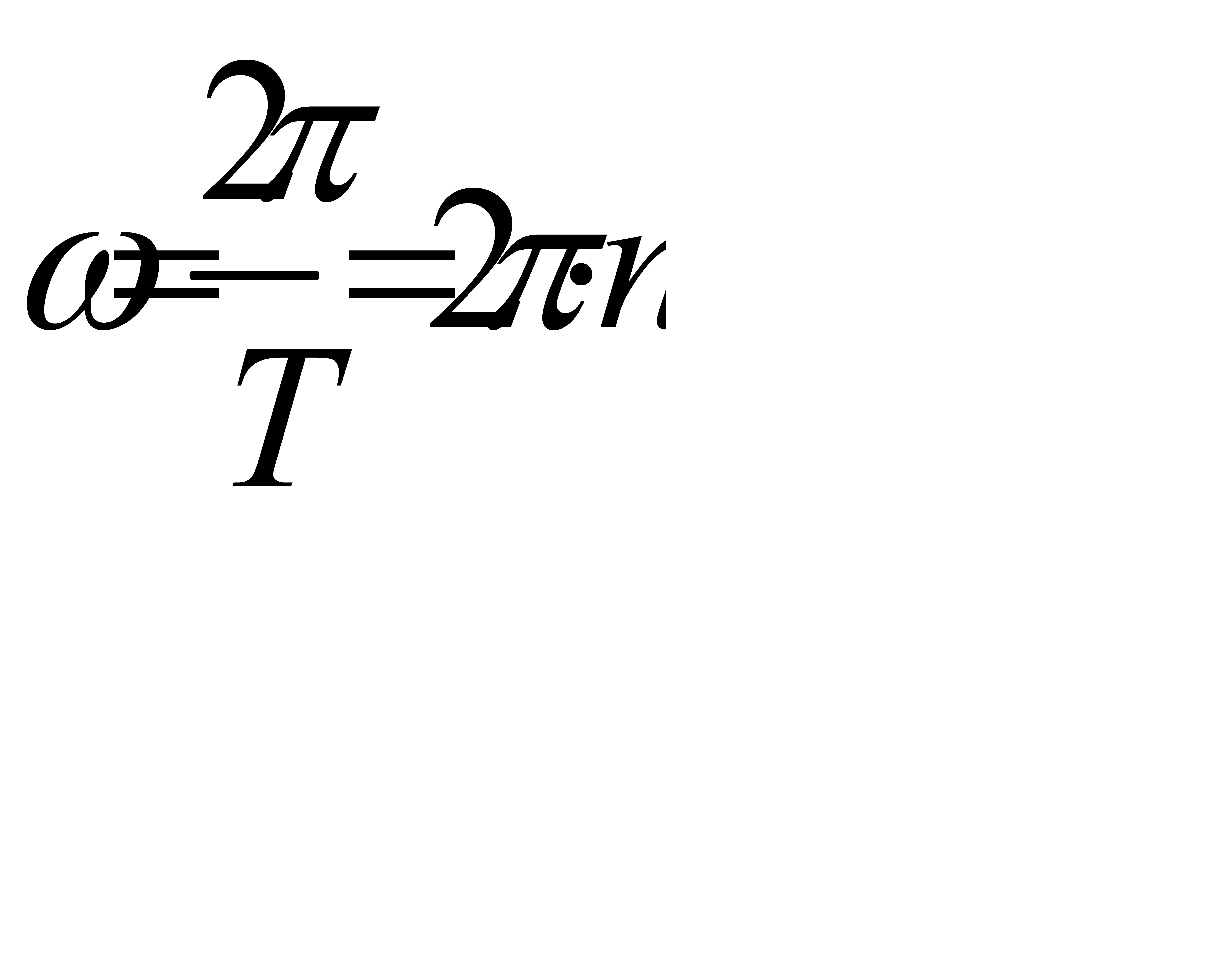 .
.
Читайте також:
- I. Фізичні основи механіки
- R – розрахунковий опір грунту основи, це такий тиск, при якому глибина зон пластичних деформацій (t) рівна 1/4b.
- VІII. Основи молекулярної фізики і термодинаміки
- Активне управління інвестиційним портфелем - теоретичні основи.
- АКУСТИКА. ЕЛЕМЕНТИ ФІЗИКИ СЛУХУ. ОСНОВИ АУДІОМЕТРІЇ
- Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
- Анатомо-фізіологічні основи статевого розвитку.
- Біологічні основи мислительної діяльності.
- Біомеханічні основи шинування при пародонтозі.
- БІОФІЗИЧНІ ОСНОВИ ЗОРОВОЇ РЕЦЕПЦІЇ
- Біохімічні основи розвитку витривалості
- Біохімічні основи розвитку силових і швидкісних якостей
| <== попередня сторінка | | | наступна сторінка ==> |
| I. Фізичні основи механіки | | | Абсолютні і відносні швидкості |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |