Окремі випадки перерізу

1. Січна площина займає окреме положення (рис. 79, а, б).

а) поверхня гранна б) поверхня обертання

Рисунок 79 – Переріз поверхні січною площиною окремого положення

Вихідна проекція лінії перерізу знаходиться на П₂ і належить сліду проекції α₂. Для гранних поверхонь визначаємо точки перерізу з відповідними ребрами – 1,2,3. Лінія перерізу – ламана лінія (трикутник). В гранях, які є видимі на П₁, лінія взаємного перерізу видима. Грань BSC на П₁ невидима, значить, лінія 2₁3₁ також невидима.

Висновок: у випадку, коли площина займає окреме положення, лінія перерізу належить сліду січної площини та визначається за сукупністю точок, які належать поверхні.

Вихідна проекція лінії перерізу знаходиться на П₁і належить сліду проекції α₁. Для кривих поверхонь визначаємо сукупність точок, кожна з яких отримана як точка, що належить поверхні тора. Точка 4 – найвища, вона отримана на перетині перпендикуляра, що проведений від осі обертання і₁ до сліду площини ∑₁. Точка 4 знаходиться на межі видимості (головному меридіані), тому лінія 1, 2, 3, 4, 5 на П₂ видима, решта – невидимі.

2. Січна площина займає загальне положення, а бічна поверхня - проекціювальне положення (рис. 80, а, б).

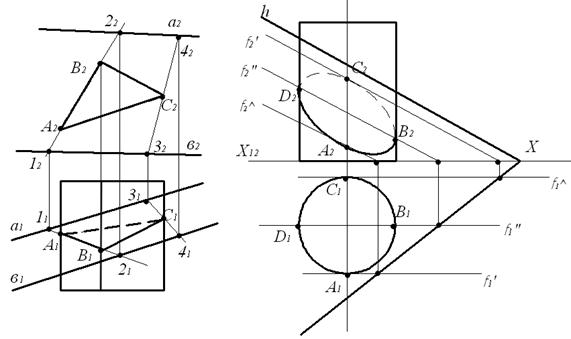
а) ∑(а║b) б) ∑(f⁰∩h ⁰)

Рисунок 80 – Переріз поверхні, бічна поверхня якої займає окреме положення, з площиною загального положення

Оскільки бічні поверхні призми (ребра перпендикулярні до П₂) та циліндра обертання (твірні перпендикулярні до П₁) вироджуються в лінію (трикутник - для призми; коло – для циліндра), то проекція лінії взаємного

перерізу на одній із площин проекцій відома і є вихідною.

Вихідна проекція лінії перерізу знаходиться на П_2.Відсутні проекції точок А,В, С знаходять на прямих [1, 2] та [3, 4], що належать площині ∑(а║b).

Вихідна проекція лінії перерізу знаходиться на П₁. Відсутні проекції точок еліпса знаходять за допомогою ліній рівня (фронталей), які належать площині ∑(f ⁰∩h⁰).

Висновок:у випадку, коли бічна поверхня займає проекціювальне положення, то лінія перерізу належить цій бічній поверхні і її точки визначаються з умови, що вони належать заданій площині.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
	\|	Конічні перерізи

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.