• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Теоретичні відомості

В розгалуженому колі струми неможливо визначити тільки за допомогою закону Ома. Їх знаходять за допомогою загальних правил Кірхгофа.

Перше правило Кірхгофа. Алгебраїчна сума струмів гілок, з’єднаних в один вузол, дорівнює нулю, тобто

. (8.1)

Вузлом називається точка, в якій сходяться більш, ніж два провідника (рис.8.1). При цьому токи в гілках, що напрямлені від вузла приймають за додатні, а токи, що напрямлені до вузла, – від’ємні. Рівняння (8.1) являється наслідком принципу неперервності токів провідності (у вузлі електричного кола не може бути накопичення електричного заряду).

Оскільки для цього вузла , перше правило Кірхгофа можна сформулювати: сума струмів, напрямлених до вузла електричного кола, дорівнює сумі струмів, напрямлених від нього. Так, для вузла А на рис.8.1 маємо:

. (8.2)

Друге правило Кірхгофа. У будь-якому замкнутому контурі розгалуженого електричного кола постійного струму алгебраїчна сума ЕРС дорівнює алгебраїчній сумі спаду напруги в усіх резистивних елементах контуру:

. (8.3)

Це співвідношення є наслідком закону збереження енергії.

Розглянемо зміну потенціалу в замкненому контурі АВС розгалуженого кола (рис.8.2), напрям обходу в якому довільно прийнято за годинниковою стрілкою.

Так як струм на ділянці кола без джерела живлення завжди спрямований в бік зменшення потенціалу, то потенціал точки А більший за потенціал точки В на величину спаду напруги на елементі R₁ (U_AB=R₁I₁), тобто

(8.4)

На ділянці ВС за напрямом обходу контуру (від В до С) потенціал зменшується на величину спаду напруги на елементі R₂, а потім стрибкоподібно збільшується на величину ЕРС Е₂ за лишком спаду напруги в середині джерела з опором r_ВТ2.

Отже,

(8.5)

На ділянці СА струм I₃ та ЕРС Е₃ діють назустріч напрямку обходу контуру, тому

(8.6)

Після простих перетворень отримаємо

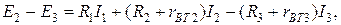(8.7)

тобто

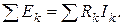(8.8)

При складанні рівнянь за другим правилом Кірхгофа додатними приймають ЕРС Е та спад напруги , якщо напрям ЕРС та струму співпадають з напрямом обходу (в іншому разі записуються зі знаком “мінус”).

Читайте також:

1. II.ТЕОРЕТИЧНІ ПИТАННЯ КУРСОВОЇ РОБОТИ
2. IX. Відомості про військовий облік
3. IX. Відомості про військовий облік
4. Q Конституція України від 28 червня 1996 р. // Відомості Верховної Ради України – 1996 - № 30 – Ст. 141
5. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
6. Активне управління інвестиційним портфелем - теоретичні основи.
7. Білковий обмін: загальні відомості
8. Біографічні відомості
9. Боротьба з проявами національної самосвідомості
10. Вальниці ковзання. Загальні відомості
11. Види правосвідомості
12. Виникнення і розвиток свідомості у людини.

Переглядів: 427