• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Теоретичні відомості

При вивченні законів обертального руху запроваджується поняття про момент інерції твердого тіла. Моментом інерції матеріальної точки (І) відносно даної вісі обертання називають величину, яка дорівнює добутку маси матеріальної точки (т) та квадрату її відстані від осі обертання (r):

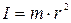. (5.1)

При обертанні навколо даної вісі не матеріальної точки, а цілого твердого тіла, можна розглядати тверде тіло як систему жорстко зв’язаних між собою матеріальних точок з масами m₁, m₂ …m_n, які розташовані на відстані r₁, r₂ …r_n від вісі обертання. Моментом інерції тіла називають суму моментів усіх матеріальних точок тіла:

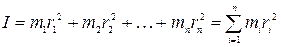. (5.2)

Моменти інерції тіл правильної геометричної форми та однорідних за складом визначають за допомогою розрахунків. Наприклад, момент інерції суцільного диска або циліндра відносно осі, яка проходить крізь його геометричний центр, дорівнює

. (5.3)

де m – маса диска (циліндра); r – радіус тіла.

Безпосереднє знаходження моменту інерції тіла неправильної (довільної) геометричної форми досить ускладнене. Гаус запропонував знаходити момент інерції тіла довільної форми шляхом порівняння періодів крутильних коливань цього тіла з періодом коливань тіла правильної геометричної форми, момент інерції якого відомий.

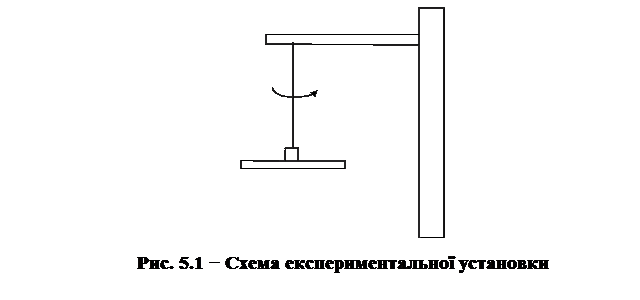Прилад для даної роботи складаються з однорідного металевого диска, який підвішений на кінці металевого дроту, закріпленого зверху на кронштейні (рис.5.1).

Якщо диск здійснює крутильні коливання, то спостерігаючи їх можна виміряти період таких коливань Т.

Нехай період крутильних коливань диска дорівнює Т₀. Залежність між періодом крутильних коливань тіла та модулем крутіння дроту, на який підвішене тіло, має вигляд:

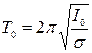, (5.4)

де: Т₀ – період крутильних коливань диска; I₀ – момент інерції диска відносно осі обертання, який можна визначити за формулою (5.3); s – модуль крутіння дроту.

На диск кладуть тверде тіло, момент інерції якого (І) треба знайти. Тепер момент інерції всієї системи відрізняється від I₀ та від I і дорівнює сумі моментів інерції обох тіл:

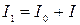(5.5)

Одержану систему тіл приводять до крутильного коливального руху і визначають період коливання системи Т₁:

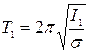. (5.6)

У виразах (5.4) та (5.5) значення модуля крутіння одне й теж саме, оскільки підвіс системи незмінний. Відношення періодів коливань диска та системи буде мати вигляд:

. (5.7)

Далі отриманий вираз зведемо до квадрату та з урахуванням формули (5.5) отримаємо:

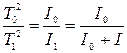. (5.8)

З даного виразу отримуємо кінцеву робочу формулу:

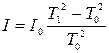. (5.9)

За цією формулою можна визначати момент інерції тіл довільної геометричної форми.

Читайте також:

1. II.ТЕОРЕТИЧНІ ПИТАННЯ КУРСОВОЇ РОБОТИ
2. IX. Відомості про військовий облік
3. IX. Відомості про військовий облік
4. Q Конституція України від 28 червня 1996 р. // Відомості Верховної Ради України – 1996 - № 30 – Ст. 141
5. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
6. Активне управління інвестиційним портфелем - теоретичні основи.
7. Білковий обмін: загальні відомості
8. Біографічні відомості
9. Боротьба з проявами національної самосвідомості
10. Вальниці ковзання. Загальні відомості
11. Види правосвідомості
12. Виникнення і розвиток свідомості у людини.

Переглядів: 845