• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Критерій мінімаксного ризику Севіджа

Виникають ситуації, в яких неконтрольовані фактори діють більш приємним чином у порівнянні з найкращім становищем, на яке орієнтувалась ОПР. Наприклад, погодні умови сказалися краще прогнозованих; конкуренція зменшилась на ринку у по­рівнянні з прогнозованими очікуваннями. У цих умовах виникає необхідність визначення можливих відхилень отриманих резуль­татів від їх оптимальних значень. У цьому випадку застосовують критерій Севіджа.

Цей критерій аналогічний попередньому критерію Вальда, але ОПР використовує не матрицю виграшів А, а матрицю ризиків R .

За критерієм Севіджа кращим є рішення, при якому макси­мальне значення ризику буде найменшим, тобто

Тобто розглядаючи i-ту стратегію, допускаємо ситуацію максимального ризику та вибираємо стратегію з найменшим ризиком .

Для застосування критерію Севіджа до ситуації пред'являються ті ж самі умови, що й для критерію Вальда.

Приклад 3.6. Для вихідних даних прикладу 3.2 за критерієм Севіджа вибрати стратегію, яка є найбільш вигідною.

Матриця ефективності ефективності за задачею 3.2.

Для кожної стратегії статистика (гравця) А знайдемо максимальний виграш 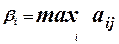, тобто (серед елементів першого стовпчика матриці наслідків обрали більше); аналогічно , , , .

Використовуючи формулу побудуємо матрицю:

Розв'язання. Запишемо матрицю ризиків гри у вигляді таблиці 3.7 і знайдемо найбільше значення для кожного рядка.

Таблиця 3.7

Матриця ризиків гри

	П1	П2	П3	П4	λ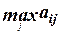
А1
А2
А3
0<λ<1

Слід вибрати таку стратегію серед стратегій , яка має найменший ризик, тому за формулою (3.18) маємо:

тобто вибираємо стратегію А₃, при застосуванні якої статисти­ком величина ризику, що дорівнює 4 одиниці, приймає мінімальне значення у самій гіршій ситуації.

Помітимо, що цей вибір оптимальної стратегії збігається з ви­бором за критеріями Вальда і оптимізму.

Суть критерію Севіджа полягає у прагненні уникнути великого ризику при виборі рішення (стратегії).

Читайте також:

1. II. Критерій найбільших лінійних деформацій
2. IV. Критерій питомої потенціальної енергії деформації формозміни
3. ReM – модифікований критерій Рейнольда, який визначається за формулою
4. Абстрактна небезпека і концепція допустимого ризику.
5. Аналiз ризику методами iмiтацiйного моделювання
6. Аналіз втрат від маркетингового ризику
7. Аналіз ефективності реальних інвестиційних проектів в умовах ризику
8. Аналіз кредитного ризику банку
9. Аналіз невизначеності і ризику
10. Аналіз ризику в життєдіяльності людини.
11. Аналіз ризику виникнення небезпеки
12. Аналіз ризику можливих збитків

Переглядів: 848