Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Середні величини.

Середні величини – це узагальнююча міра ознаки, що варіює, у статистичній сукупності, тобто це узагальнюючий показник, який характеризує типовий рівень ознаки , що варіює, в розрахунку на одиницю сукупності.

Середня величина - узагальнюючий показник. Який характеризує сукупність однотипних явищ за змінною кількісною ознакою. Середня величина показує типове, характерне значення ознаки, віднесене до одиниць статистичної сукупності.

Умови наукового використання середніх величин:

- якісна однорідність сукупності;

- сукупність має бути достатньо великою;

- використання загальних середніх з груповими.

Призначення середніх в економічному аналізі:

- характеристика рівня масових суспільних явищ;

- проведення порівняльного аналізу;

- вивчення тенденцій розвитку явищ;

- вибіркове спостереження;

- вимірювання взаємозв’язків.

В статистиці використовують різні види середніх величин. Застосування того чи іншого виду середньої залежить від виду ряду розподілу. Змісту ознаки і мети використання. Критерієм правильного вибору виду середньої величини є запис логічної формули розрахунку.

Статистика розглядає наступні види середніх величин:

- середня арифметична,

- середня гармонійна,

- середня геометрична,

- середня квадратична

Кожна з цих середніх може розраховуватися як для не згрупованих даних – проста середня, так і для згрупованих даних – зважена середня.

- середня хронологічна,

- порядкові середні (мода, медіана, квартилі, децилі).

Розрахункові формули, мету застосування і критерій застосування того чи іншого виду середньої величини подамо у таблиці.

Вид середньої	Критерій вибору виду	Розрахункова формула	Інша інформація
простої	зваженої
Середня арифметична	Є однією з найбільш поширених середніх. Її використовують для характеристики рядів розподілу, сума окремих значень ознаки в яких утворює загальний обсяг ознаки. Інакше, використовується за первинними не згрупованими (проста) або згрупованими (зважена) даними коли, відповідно, відомо і чисельник і знаменник логічної формули, не відомо чисельник а відомо знаменник . 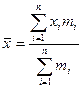Логічна формула : середня = загальний обсяг ознаки/загальний обсяг сукупності			Для визначення середньої в інтервальному варіаційному ряді необхідно попередньо визначити серединні ( центральні0 значення варіант як середину інтервалу , переходячи до дискретного ряду і застосувати середню зважену. Якщо при цьому початковий інтервал є відкритим, то його довжина відповідає довжині наступного інтервалу, і якщо відкритим є останній інтервал, то довжина його відповідає довжини попереднього інтервалу. Властивості. - Середня сталої величини дорівнює цій сталій: - Якщо кожну з варіант ряду розподілу збільшити ( зменшити) на певну сталу величину А. 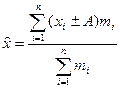то і середня зміниться на цю величину: , -Якщо кожну з варіант ряду розподілу помножити (розділити) на певну сталу величину А, то і середня зміниться на цю величину: 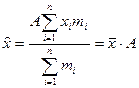-Якщо усі частоти помножити (розділити) на певну сталу величину, то середня від цього не зміниться: - Сума відхилень варіант від середньої дорівнює нулю: - сума квадратів відхилень значень варіант від середньої є меншою за суму квадратів відхилень від будь-якої іншої величини6 З урахуванням цих властивостей обчислення середньої арифметичної для інтервального варіаційного ряду з рівними інтервалами можна виконати методом моментів першого порядку за такою формулою: , -довжина інтервалу, А- «умовний нуль» або центральне значення ознаки з найвищою частотою, - момент першого порядку, - центральне значення ознаки у відповідному інтервалі.
Середня гармонійна	Є величиною, яка обернена до середньої арифметичної. Має складнішу конструкцію і використовується у випадках, коли за частоти береться добутки значень варіант ознаки на їх чисельність( . Середня гармонійна вживається тоді, коли не задано обсягу сукупності а задано обсяг значень ознаки( варіанти 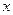зважуються за значеннями ). Інакше. Середня гармонійна використовується за не згрупованими та згрупованими даними коли в логічній формулі середньої відомо чисельник а невідомо знаменник		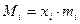- обсяг значень ознаки
Середня геометрична	Використовується, якщо визначальна властивість сукупності (обсяг значень ознаки) формується як добуток індивідуальних значень ознаки. Найбільш широко використовується при аналізі рядів динаміки з метою визначення середніх коефіцієнтів (темпів) зміни рівнів ряду.
Середня квадратична	Використовується при визначенні абсолютних і відносних показників варіації. Середня квадратична використовується у випадку сумування квадратів значень варіант
Середня хронологічна	Використовується у рядах динаміки при визначенні середнього рівня моментного ряду. Якщо у хронологічному ряду наведено моментні показники, то для обчислення середньої вони замінюються пів сумами значень на початок і кінець періоду. Якщо моментів більш ніж два і інтервали між ними рівні. То середня обчислюється за середньою хронологічною.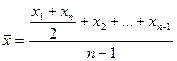
Порядкові середні	Використовуються при визначенні характеристик рядів розподілу і форм розподілу	Дискретний ряд розподілу	Інтервальний ряд розподілу
Мода	Значення варіанти, яке найчастіше зустрічається в ряді розподілу.( Найбільш поширене значення ознаки, домінанта0	В ряді розподілу знайти максимальну частоту 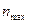і значення варіанти, яке відповідає цій частоті і буде модою	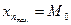В ряді розподілу знайти модальний інтервал, інтервал з максимальною частотою. У цьому інтервалі моду знайти за формулою:
Медіана	Значення варіанти, яке припадає на середину впорядкованого ряду розподілу, поділяє його навпіл – на дві рівні за обсягом частини	Визначають використовуючи кумулятивні частоти 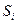. Серед всіх кумулятивних частот знаходять таку, яка не менша за половину обсягу сукупності тобто таку, що . Варіанта, яка відповідатиме їй і буде медіаною.	Визначаютьмедіанний інтервал як інтервал з кумулятивною частотою не меншою за половину обсягу сукупності. В медіанному інтервалі медіану шукають за формулою
Квартилі	Значення варіант , які поділяють сукупність на чотири рівні за обсягом частини. Є три . Другий дорівнює медіані.	Визначають використовуючи кумулятивні частоти 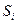. Серед всіх кумулятивних частот знаходять таку, яка не менша за j/4 обсягу сукупності тобто таку, що . Варіанта, яка відповідатиме їй і буде відповідним квартелем. .	Визначаютьквартильний інтервал як інтервал з кумулятивною частотою не меншою за j/4 обсягу сукупності. В інтервалі квартилі шукають за формулою
Децилі	Значення варіант , які поділяють сукупність на десять рівних за обсягом частини Є дев'ять. П'ятий дорівнює медіані	Аналогічно до медіани і квартилів	Аналогічно до медіани і квартилів

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Відносні величини динаміки	\|	Тема № Ряди розподілу. Аналіз варіації та форм розподілу.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.