Теоретичні відомості

Задача наближення функції виникає, коли для функції, даної при дискретних значеннях аргументу у вигляді таблиці (ці значення називаються вузлами інтерполяції) необхідно знайти значення функції в проміжних крапках. Накладаючи вимогу, щоб наближена функція у вузлах співпадала з табличними значеннями (рис. 4.1), одержуємо задачу інтерполяції.

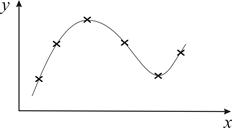
Рисунок 4.1 – Графік наближеної функції

Нехай в результаті спостережень за ходом деякого процесу побудована таблиця:

x	x₀	x₁	x₂	…	x_n
f(x)	f(x₀)	f(x₁)	f(x₂)	…	f(x_n)

Тобто, функція f(x) задана таблицею значень для кінцевої безлічі значень х .

Якщо необхідно знайти значення f(x) для проміжного значення аргументу, то будують функцію φ(x) , просту для обчислень і таку, що для заданих x₀ , x₁ , x₂ , ... , x_n приймає значення f(x₀) , f(x₁) , f(x₂) , ... , f(x_n) .

В інших точках відрізка [x_0, x_n] вважаємо, що φ(x) приблизно визначає функцію f(x) з тим чи іншим ступенем точності.

Найчастіше, функцію φ(x) представляють у вигляді алгебраїчного багаточлена деякого ступеня.

Найпростіша інтерполяція – це лінійна, тобто, коли невідому аналітичну залежність f(x) замінюють відрізками прямих, які проходять через відповідні вузли інтерполяції. В цьому випадку потрібно визначити якому відрізку належить надане х^* і за формулою лінійної інтерполяції знаходять f(x^*) . Якщо x_i <= x^* <= x_i₊₁ , то відповідна пряма проходить через вузли (x_i , f(x_і)) , (x_i₊₁ , f(x_і+1)) :

(4.1)

Точність підрахунків в цьому випадку незначна, тому що враховується вплив тільки 2-ох вузлів інтерполяції. Частіше будують багаточлен P_n(x) ступеня n , що в (n+1) даних точках x₀ , x₁ , x₂ , ... , x_n . приймає дані значення y₀ = f(x₀) , y₁ = f(x₁) , … , y_n = f(x_n) , тобто

f(x_і) = P_n(x_і) , (і = 0, 1, 2, ... , n) .

Відзначимо, що двох різних інтерполяційних багаточленів одного і того же ступеня n існувати не може. Цим умовам задовольняє інтерполяційний багаточлен Лагранжа:

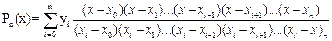(4.2)

Тоді

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
ЛАБОРАТОРНА РОБОТА №4	\|	Індивідуальні завдання

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.