Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Види економіко-математичних моделей оптимізації

При здійсненні господарської діяльності підприємством можуть бути сформовані наступні види економіко-математичних моделей оптимізації:

1. Економіко-математичні моделі оптимізації випуску продукції.

2. Економіко-математичні моделі розподілу фінансових ресурсів по оптимізації зростання потужностей підприємства.

3. Економіко-математична модель розподілу капітальних вкладень.

Економіко-математичні моделі оптимізації випуску продукції розробляються для максимізації прибутку від реалізації продукції. В загальному вигляді ця функція моделі має наступний вигляд:

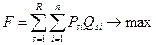, (2.9)

де 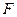- функція максимізації прибутку;

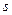- номер, вид виробляємої продукції;

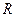- кількість видів продукції;

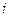- номер підприємства;

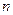- кількість підприємств;

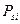- прибуток від реалізації одиниці продукції 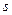на 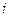-ому підприємстві;

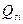- обсяг 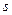виду продукції на 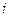-ому підприємстві.

При цьому використовуються наступні обмеження:

1. Обсяг споживання ресурсів не повинен 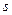виду продукції не повинен перевищувати загальний обсяг використаних ресурсів на підприємстві.

2. Обсяг 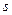виду виробленої продукції дорівнює плану випуску цієї продукції.

3. Обсяг 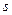виду виробленої продукції знаходиться між нижньою і верхньою границею виробництва цієї продукції на 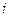-ому підприємстві.

4. Обсяг 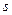виду виробленої продукції на 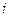-ому підприємстві перевищує нуль.

В основі економіко-математичної моделі розподілу фінансових ресурсів по оптимізації зростання потужностей підприємства є наступна функція:

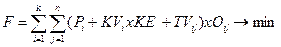, (2.10)

де 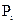- вартість одиниці продукції i-го постачальника;

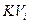- капітальні витрати на одиницю готової продукції;

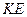- коефіцієнт ефективності капітальних вкладень;

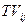- транспортні витрати по перевезенню одиниці продукції i-го постачальника j покупцю;

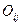- обсяг поставок продукції i-го постачальника j покупцю.

При цьому вводяться наступні обмеження:

1. Обсяг поставок продукції i-го постачальника j покупцю не перевищує потужність i-го постачальника.

2. Обсяг поставок продукції i-го постачальника j покупцю дорівнює попиту j покупця.

3. Обсяг поставок продукції i-го постачальника j покупцю дорвінює або перевищує нуль.

При побудові економіко-математичної моделі розподілу капітальних вкладень по проектам враховується функція, яка полягає в максимізації можливого дохіду від реалізації j варіанту капітальних вкладень ( ):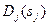

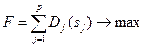, (2.11)

де р - загальна кількість проектів;

j - варіант (індекс) проекту капітальних вкладень;

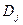- можливий дохід від реалізації j варіанту капітальних вкладень.

Обмеження для виконання цієї функції наступні:

1. Загальна кількість варіантів капітальних вкладень повинна перевищувати або дорівнювати кількості видів продукції.

2. Обсяг капітальних вкладень по j варіанту не повинен перевищувати загальний річний обсяг капітальних вкладень.

3. Якщо обсяг виробляємої продукції досягає одиниці, то проект приймається, якщо цей обсяг дорівнює нулю – проект відхиляється.

В економічному моделюванні використовують і розв’язують задачи безумовної оптимізації, в яких задається лише одна цільова функція. В задачах безумовної оптимізації не існує обмежень і граничних умов. У цих задачах поняття оптимуму та екстремуму збігаються, і для знаходження оптимуму в них застосовуються методи знаходження екстремуму. Слід відзначити, що найбільше або найменше значення це екстремум, а оптимум – оптимальне найбільше або найменше значення.

В цих задачах знаходяться першу похідну функції, дорівнюють її до нуля, знайти парамтери моделі, знайти другу похідну і визначити її знак. Якщо друга похідна більша за 0, то точка х — мінімум функції.

Методами розв'язання задач умовної оптимізації:

1. Метод штрафних функцій, в якій мінімізується нова цільова функція, яка містить у собі першу цільову функцію та задані обмеження. При цьому визначається штрафна функція.

2. Метод Лагранжа – полягає у побудові функції виду: L(x_x, х₂, X) =f(x_v х₂) + Xg(x_v х₂), тобто, зведення задачі на умовний екстремум двох незалежних змінних до задачі на абсолютний екстремум функції L{xy, x₂, X) трьох незалежних змінних х₁, х₂, X. Функція Лагранжа є сумою цільової функції та функції обмеження, помноженої на нову незалежну змінну X (множник Лагранжа), яка має перший порядок. Для знаходження точок умовного локального екстремуму функції за наявності обмеження слід насамперед знайти критичні точки функції Лагранжа. Потім критичні точки функції Лагранжа потрібно скоротити на координати X. Потім кожну одержану скорочену точку необхідно проаналізувати, чи є вона точкою умовного екстремуму функції за даних обмеженнях чи ні.

Питання та завдання для самоконтролю до змістового модуля 1

Питання для самоконтролю:

1. Що таке економіко-математичне моделювання?

2. Назвіть етапи розвитку економіко-математичного моделювання?

3. Визначте поняття «Модель» і які види моделей Ви можете назвати.

4. Назвіть основні етапи моделювання?

5. Які види явищ Ви знаєте?

6. Визначте випадкову величину і її числову характеристику?

7. Назвіть і охарактеризуйте закони розподілу випадкової величини?

8. Як перевіряють статистичні гіпотези?

9. Назвіть етапи попередньої обробки інформації?

10. Охарактеризуйте оптимізаційні моделі і назвіть їх види.

11. В чому полягають задачі умовної і безумовної оптимізації.

12. Які методи використовуються для вирішення задач умовної і безумовної оптимізації і в чому вони полягають.

13. В чому полягають економіко-математичні моделі оптимізації випуску продукції, розподілу фінансових ресурсів по оптимізації зростання потужностей підприємства, розподілу капітальних вкладень по проектам.

Завдання для самоконтролю:

1. Встановити, при якому обсязі спостережень n вибірка є генеральною сукупністю, якщо Р=0,95 або 95%, 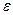=0,80 і 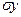=4,18?

2. Є вибірка обсягом n=100 спостережень. Середнє значення по вибірці 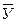= 10,12; середнє квадратичне відхилення 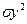=5,12; рівень значущості 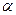=0,05; максимальне значення ознаки у_mах=26,16; мінімальне - у_mіn=3,09. Визначити можливість використання в подальших дослідженнях у_mах і у_mіn.

3. По двох об'єктах зібрана інформація з наступними кількісними характеристиками: n₁=45; n₂=46; 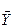₁=15,17; 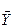₂=12,5; σ_y1²=61,4; σ_y2²=55,6. Визначте рівень значимості при формуванні гіпотези про однорідність сукупності вибіркових даних.

4. Визначити закон розподілу витрат часу проходження рухомим складом маршруту між двома зупинками (хвил.) при n=190 спостережень і y_min=0,50 хв., y_max=1,46 хв. Розмір інтервалу складає 0,1. Побудуйте гістограму і полігон розподілу. Розрахуйте показники нормального закону розподілу.

5. Знайдіть екстремум функції випуску продукції у вигляді у = f(x) аналітичним методом.

6. Знайдіть екстремум функції у = х₁ + х₂ за умови х₁ + х₂- 1 = 0 або розв’яжіть задачу на умовний екстремум методом Лагранжа.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Загальна характеристика задач математичного програмування	\|	Зиістовий модуль 2

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.