• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Залежна змінна для такої моделі розглядається, як ендогенна змінна, а незалежні змінні – як екзогенні.

Теоретична узагальнена лінійна економетрична модель може бути специфікована у наступній формі :

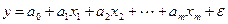, (11.4)

де y – залежна (пояснювана) змінна моделі, x₁, x₂, … , x_m – незалежні (пояснюючі) змінні моделі або фактори, а₀, а₁, …. , а_m – параметри моделі, ε – випадковий член, m – кількість пояснюючих змінних моделі.

Представлена узагальнена модель (11.4) дійсна для всієї генеральної сукупності спостережень за змінними моделі й відображає відповідну економічну ситуацію, яка склалась на макро- або мікрорівні.

Вибіркова узагальнена лінійна економетрична модель має наступний вигляд :

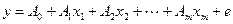, (11.5)

де y – залежна (пояснювана) змінна моделі, x₁, x₂, … , x_m – незалежні (пояснюючі) змінні моделі (фактори), А₀, А₁, А_m – параметри вибіркової моделі, e – залишки моделі.

Вибіркова модель (11.5) розробляється для певної статистичної вибірки з генеральної сукупності. На відміну від моделі (11.4) параметри вибіркової моделі А₀, А₁, … , А_m є оцінками (наближеними значеннями) параметрів а₀, а₁, а_m і випадковими величинами, а залишки моделі e можна оцінити на основі статистичних даних. Таким чином, вибіркова модель завжди є тільки оцінкою реальної але невідомої теоретичної моделі.

Вибіркова функція регресії для узагальненої лінійної економетричної моделі має наступний вигляд :

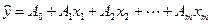, (11.6)

де 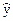– оцінка математичного сподівання залежної (пояснюваної) змінної моделі, x₁, x₂, … , x_m – незалежні (пояснюючі) змінні моделі (фактори), А₀, А₁, А_m – параметри вибіркової регресії.

Узагальнена нелінійна економетрична модель - це регресійна модель, яка встановлює нелінійну залежність між економічними показниками.

Узагальненими нелінійними економетричними моделями можуть бути відомі функції:

1. Квадратична - 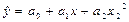або .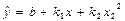

2. Гіперболічна - 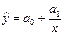або .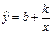

3. Степенева - 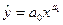або .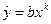

4. Модифікована експонента - 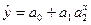або .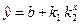

5. Крива Гомперця - 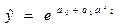або .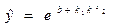

6. Логістична - 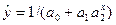або .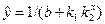

7. Показова функція - 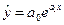або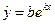

Більшість представлених функцій, що використовуються для опису техніко-економічних показників, шляхом функціональних перетворень у по х (роздільно або одночасно) можуть бути зведені до лінійного вигляду. При цьому метод перетворень залежить від форми зв'язку.

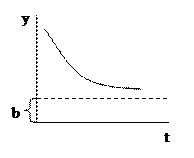Гіпербола вигляду 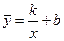перетвориться в лінійну шляхом заміни. Статична функція вигляду 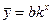перетвориться в лінійну шляхом логарифмуванням. У результаті маємо 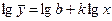. Позначимо .

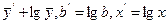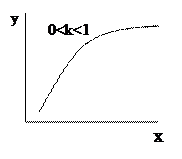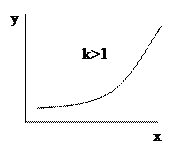У результаті маємо .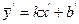

Показова функція виду y=be^kx перетвориться в лінійну логарифмуванням .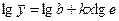

Позначимо 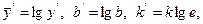при цьому 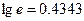. У результаті маємо y₁х+b₁.

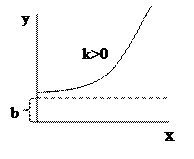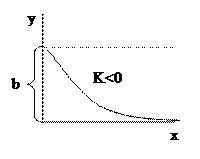Теоретична лінія регресії може бути подана у вигляді плавної кривої яка кількісно виражає зв'язок між середніми інтервальними значеннями 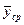і відповідними значеннями х (аргументами). Процес знаходження невідомих параметрів теоретичної залежності є однією з важливих проблем теорії кореляції і регресії.

Наприклад, при знаходженні параметрів параболи виду 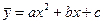необхідно складати і вирішувати систему з трьох нормальних рівнянь, яке розв’язується, виходячи з вимоги методу найменших квадратів, тобто .

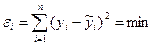Підставляючи 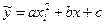, маємо

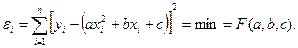(11.7)

Знаходимо часткові похідні 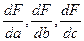і прирівнюємо їх до нуля

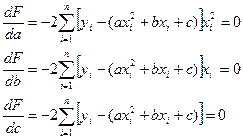(11.8)

Після відповідного перетворення маємо

(11.9)

В узагальнених економетричних моделях визначаються також коефіцієнти кореляції, детермінації, критерії адекватності (t-статистики, F-критерій Фішера, перевіряється на мультиколінеарність, гетероскедастичність, автокореляцію залишків).

Читайте також:

1. CMM. Визначення моделі зрілості.
2. III. GPSS — програма імітаційної моделі ЕОМ
3. ISO 15504.Структура еталонної моделі
4. Абвяшчэнне незалежнасці Рэспублікі Беларусь.
5. Абвяшчэнне незалежнасці Рэспублікі Беларусь.
6. Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
7. Авторегресійні моделі в аналізі динаміки економічних процесів і їх прогнозуванні
8. Алгоритм реалізації моделі
9. Алгоритм реалізації моделі
10. Алгоритм реалізації моделі
11. Алгоритм реалізації моделі
12. Алгоритм реалізації моделі

Переглядів: 645