• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Точність оцінки ймовірності за допомогою відносної частоти.

Точність методу можна визначити, коли ймовірність оцінюється з допомогою відносної частоти. З такими задачами часто стикаються при імітаційному моделюванні.

Нехай моделюються появи випадкової події A, імовірність якої дорівнює p.

Візьмемо якщо при i-й спробі настала подія A, і коли подія A не настала. Отже, загальна кількість спроб, в яких настала подія A, подається так:

(5.6)

де n — загальне число спроб.

Оскільки розглядається схема незалежних випробувань, то відносна частота появи події A є випадкова величина, яка при досить великому n має розподіл, близький до нормального.

Для нормально розподіленої випадкової величини виконується правило «трьох сигм»:

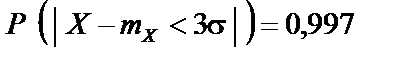. (5.7)

Тому для практичних розрахунків праву частину цієї рівності вважають такою, що дорівнює одиниці, а дослідні дані, які не задовольняють зазначену умову, відкидаються як такі, що не мають імовірнісного характеру.

Для випадку, що розглядається, Знайдемо математичне сподівання даної величини та середнє квадратичне s :

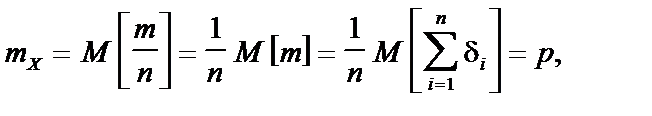
Згідно з (5.7) маємо

. (5.8)

Позначивши символом e помилку визначення p, тобто дістанемо , або

(5.9)

Звідси

(5.10)

4. Рівномірна випадкова послідовність чисел РВП [0,1]

Випадкова величина Х має рівномірний розподіл на відрізку [a, b], коли її щільність розподілу ймовірностей має вигляд

Математичне сподівання та дисперсія випадкової величини

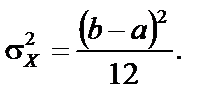
Якщо випадкова величина розподілена на відрізку [0, 1], то

(5.11)

Рівномірно розподілену на відрізку [0, 1] випадкову величину позначимо x. Для неї характерна унікальна (притаманна лише даному розподілу) властивість: імовірність того, що значення цієї випадкової величини потраплять на деякий інтервал з межами
0£a£b£ 1, дорівнює довжині цього інтервалу:

(5.12)

Ця властивість часто використовується в методі Монте-Карло як необхідна і достатня умова того, що деяка випадкова величина має розподіл (5.11).

Принципова можливість генерувати послідовні реалізації випадкової величини xвипливає з такогоперетворення:

(5.13)

де — реалізація випадкової величини Z, що набуває лише двох значень — 0 і 1 — з однаковою ймовірністю 0,5.

Можна показати, що отримувана з допомогою перетворення (5.13) випадкова величина xмає властивість (5.12). Наприклад,

Випадкову величину Z можна реалізувати, наприклад, підкиданням монети, коли вважати, що при випаданні «герба» випадкова величина набуває значення 1, а в противному разі — значення 0.

Випадкова величина x, рівномірно розподілена на відрізку [0, 1], може мати нескінченну кількість реалізацій. Проте при машинному використанні методу Монте-Карло на ЕОМ можна утворити лише випадкових чисел, що не збігаються одне з одним (k — кількість двійкових розрядів машинної пам’яті). Тому рівномірна випадкова послідовність чисел (скорочено РВП [0, 1]), використана при машинних розрахунках, фактично є реалізацією дискретної випадкової величини, розподіл якої називається квазірівномірним (від лат. quasi — майже, ніби, неначе).

Від сукупності чисел 0, 1, 2, ..., –1, які можна подати з допомогою двійкових розрядів, легко перейти до можливих значень дискретної випадкової величини x, що має квазірівномірний розподіл на інтервалі [0, 1]:

(i = 0, 1, 2,..., –1).

Читайте також:

1. II. ПОРЯДОК ПРОВЕДЕННЯ ТА ОЦІНКИ ПОТОЧНИХ ТА ПІДСУМКОВИХ ЗАНЯТЬ (ЗМІСТОВИХ МОДУЛІВ).
2. II. ПОРЯДОК ПРОВЕДЕННЯ ТА ОЦІНКИ ПОТОЧНИХ ТА ПІДСУМКОВИХ ЗАНЯТЬ (ЗМІСТОВИХ МОДУЛІВ).
3. А) Мета і об'єкти грошової оцінки
4. Адекватним фізичним критерієм оцінки її впливу на організм люди1
5. Алгоритм виявлення, оцінки та зменшення ризиків виникнення небезпечних ситуацій на виробництві ( СРС – «А»)
6. Аналіз відхилень – основний інструмент оцінки діяльності центрів відповідальності
7. Аналіз відхилень — основний інструмент оцінки діяльності центрів відповідальності
8. Аналіз економічноїї політики за допомогою моделі Мандела-Флемінга. Випадки вільного та фіксованого валютного курсів.
9. Аналіз загальної рівноваги розширює можливості оцінки ефективності функціонування ринкової економіки.
10. Аналіз методичних підходів до оцінки конкурентоспроможності фірми
11. Аналіз цін конкурентів проводиться за допомогою
12. Ануїтет та його значення для оцінки інвестицій

Переглядів: 549