Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Елементарна ланка та її характеристики. З’єднання ланок. Структурні схеми і їх перетворення.

ЛЕКЦІЯ №8

ТЕМА: „ОСНОВИ ТЕОРІЇ ЛІНІЙНИХ СИСТЕМ АВТОМАТИЧНОГО РЕГУЛЮВАННЯ”

Елементарна ланка і її характеристики

Будь-яка система автоматичного регулювання складається з ряду елементів, що виконують цілеспрямоване перетворення сигналів керування. Хоча число елементів автоматичних систем досить велике і принципи їх роботи самі різні, але загальним для них є те, що вони здійснюють передачу інформації. Щоб виявити розмаїтість елементів за їх передавальними властивостями, введене поняття елементарної ланки.

Елемент автоматичної системи або його частина, що здійснює найпростіше перетворення інформації (таке, котре не може бути замінено комбінацією інших), називається елементарною ланкою. Вид елементарної ланки визначає тільки математична залежність між вихідною і вхідною величинами х_вих=f(x_вx.) (рис. 8.1), яку називають характеристикою ланки. Якщо в елементарній ланці не відбувається нагромадження енергії або речовини, то х_вих=f(x_вx.) являє собою алгебраїчне рівняння. При нагромадженні енергії або речовини в ланці зв'язок між вихідною і вхідною величинами описується диференціальним рівнянням. Рівняння складають на підставі аналізу фізичних процесів, що протікають у ланці, і законів збереження енергії і речовини. При складанні рівняння необхідна деяка ідеалізація для того, щоб врахувати тільки основні явища і зв'язки.

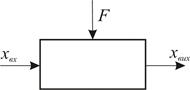
Рис. 8.1. Схематичне зображення елементарної ланки.

Реальне представлення про передавальні властивості ланки дає рішення рівняння. Знайти його можливо за умови, якщо відома вхідна величина x_вx.(t) як функція часу.

Дуже часто має місце різка зміна вхідної величини, наприклад, швидка зміна рівня води в б'єфі, включення електродвигуна тощо. При різкій (гранично миттєвій) зміні x_вx. виникає найбільша динамічна похибка в перетворенні сигналів керування. Тому в якості типового вхідного впливу на елементарну ланку приймають одиничну ступінчасту функцію

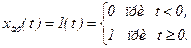/8.1/

Реакція ланки або системи на одиничний вхідний сигнал називається перехідною характеристикоюі її прийнято позначати h(t). Вона являє собою рішення рівняння ланки при і описує процес переходу від одного стану рівноваги до іншого. Тому графік перехідної характеристики іноді називають кривою розгону. Якщо відома перехідна характеристика h(t), a , де А = const, то вихідна величина .

Іноді необхідно вивчити реакцію ланки на інші впливи. Якщо, наприклад, вхідний вплив є відома функція часу φ(t), то реакцію на цей вплив знаходять за допомогою інтеграла Дюамеля:

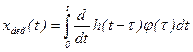. /8.2/

Використовуючи перехідну характеристику, можна також наближено визначити реакцію ланки на вхідний вплив довільної форми. Для цього необхідно апроксимувати площу, обмежену даною кривою, сумою зсунутих у часі ступінчастих впливів, як це показано на рис. 8.2. Тоді вихідна величина

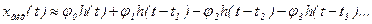/8.3/

Крім вхідного впливу, на елементарну ланку може впливати і збурення F (рис. 8.1). Реакція ланки на ступінчасте збурення F(t)=1(t) називається перехідною характеристикою за збуреннямі позначається h_F(t). Вона також є рішенням рівняння, що встановлює залежність вихідної величини від збурення.

Реакцію ланки на інші види збурень знаходять також за рівняннями /8.2/ і /8.3/, замінивши в них h(t) на h_F(t).

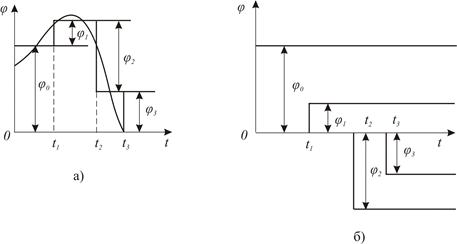
Рис. 8.2. Апроксимація функції φ(t) сумою ступінчастих функцій.

Крім опису властивостей елементів і систем за допомогою диференційних рівнянь і їхніх рішень, в теорії автоматичного регулювання широко використовують передаточні функції і частотні характеристики, на підставі яких спрощуються розрахунки параметрів систем автоматичного регулювання.

Передаточною функцією елемента називається відношення зображень за Лапласом вихідної і вхідної величин при нульових початкових умовах. Отже, для її знаходження необхідно перетворити за Лапласом лінійне або лінеаризоване рівняння ланки при нульових початкових умовах.

Для прикладу знайдемо передатну функцію регулятора циліндричного типу, що описується рівнянням

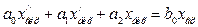. /8.4/

Зробивши перетворення рівняння /3.4/ за Лапласом при нульових початкових умовах, одержуємо:

, /8.5/

де х_вих(р), х_вх(р) - зображення вихідної і вхідної величин; p=σ+jω - комплексний аргумент (σ і ω - дійсні числа, ).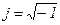

Відношення зображення вихідної величини до зображення вхідної

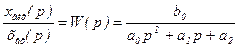/8.6/

є передаточна функція регулятора.

З порівняння /8.6/ з рівнянням /8.4/ випливає, що формально передаточу функцію легко одержати, замінивши в рівнянні /8.4/ оператор диференціювання на р.

Функція W(p) називається передаточною функцією ланки за керуючим (вхідним) впливом. Відношення

/8.7/

називається передаточною функцією за збуренням.

Якщо на вхід елементарної ланки (системи) подати вплив у виді гармонійного коливання з кутовою частотою ω і амплітудою А_вх,

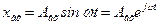, /8.8/

то в усталеному режимі вихідна величина також буде мати вигляд гармонійних коливань з кутовою частотою ω, але з амплітудою А_вих і фазою φ:

. /8.9/

При зміні кутової частоти змінюються амплітуда і фаза вихідних коливань. Відношення

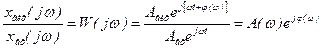/8.10/

називається амплітудно-фазовою частотною характеристикою ланки.

Характеристику 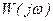можна також одержати з передаточної функції W(p), замінивши комплексну змінну р уявною величиною 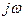. З /8.10/ випливає, що при кутовій частоті 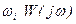являє собою вектор, модуль якого дорівнює , а фаза 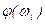. При зміні кутової частоти від нуля до нескінченності кінець вектора 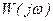описує криву, що є годографом амплітудно-фазової частотної характеристики (рис. 8.3).

Залежність Α(ω) називається амплітудною частотною характеристикою, а φ (ω) - фазовою частотною характеристикою. Ці характеристики показують, як змінюються амплітуда і фаза вихідних коливань у порівнянні з коливаннями вхідної величини. Амплітудну і фазову частотні характеристики можна зняти експериментально за допомогою спеціальної апаратури.

Рис.8.3. Годограф амплітудно-фазової частотної характеристики.

Якщо відома характеристика 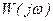, то, замінивши 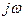на р, одержують передаточну функцію ланки. Підставивши в залежність W(p) p = d/dt, знаходять рівняння ланки.

Отже, перехідні і частотні характеристики показують реакцію ланки на різні зовнішні впливи.

Елементарні динамічні ланки

Елементи автоматичних систем, різні за фізичною природою, конструкцією, розмірами і іншими характеристиками, але описувані рівняння одного виду є однаковими динамічними ланками. Тому замість вивчення властивостей усього різномаїття елементів автоматики досить вивчити властивості елементарних ланок. Знання властивостей цих ланок значно полегшує вивчення різних систем автоматичного регулювання. Основними є наступні динамічні ланки.

Підсилююча ланка

У цієї ланки вихідна величина пропорційна вхідний

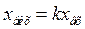, /8.11/

де k - коефіцієнт підсилення. Підсилюючу ланку ще називають пропорційною або безінерційною.

Перехідна характеристика, передаточна функція й амплітудно-фазова частотна характеристика підсилюючої ланки рівні k. Це означає, що ланка без спотворення підсилює вхідний сигнал будь-якого виду. Прикладами підсилюючої ланки можуть бути важіль, напівпровідниковий підсилювач тощо.

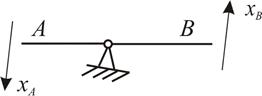
Рис. 8.4. Підсилююча ланка.

Якщо знехтувати масою важеля і вважати його абсолютно жорстким, то переміщення точок А і В (рис. 8.4) зв'язані залежністю

. /8.12/

Вихідна і вхідна напруги підсилювача на польовому транзисторі, знаходяться в співвідношенні

. /8.13/

Рівняння /8.12/ і /8.13/ одного виду. Тому ці два різні елементи є підсилюючими ланками.

Інтегруюча ланка

До інтегруючих відносяться ланки, у яких вихідна величина пропорційна інтегралу від вхідної величини:

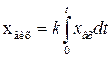, /8.14/

де k — коефіцієнт підсилення ланки.

Прикладами інтегруючих ланок є басейн, з якого вода відкачується помпою зі сталою витратою, гідравлічний підсилювач без зворотного зв’язку і інші.

Рис. 8.5. Характеристики інтегруючої ланки: а - перехідна; б - амплітудно-фазова частотна.

Перехідна характеристика ланки

/8.15/

є пряма лінія (рис. 8.5, а). Тому що h(t) - лінійна функція, то коефіцієнт k іноді називають швидкістю розгону. Передаточна функція інтегруючої ланки

W(p)=k/p.

Амплітудно-фазова частотна характеристика

і її годограф збігається з від’ємною уявною піввіссю (рис. 8.5,б). Ця характеристика показує, що зі збільшенням кутової частоти амплітуди 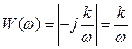вихідних коливань у порівнянні з вхідними зменшуються, а фаза коливань не залежить від ω.

Диференціююча ланка

Диференціюючою є ланка, вихідна величина якої пропорційна похідній вхідної величини:

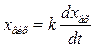, /8.16/

де k — коефіцієнт пропорційності.

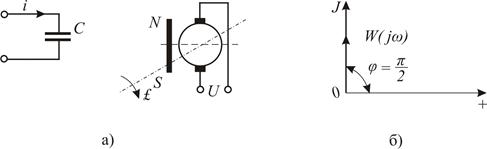
Рис. 8.6. Диференціюючі ланки (а) і їх амплітудно-фазова частотна характеристика (б).

Прикладами таких ланок є електричний конденсатор, тахогенератор тощо (рис. 3.6, а). Дійсно, струм у ємності

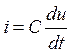, /8.17/

де С і u – ємність і напруга на конденсаторі, напруга на затискачах тахогенератора

, /8.18/

де ω_Т - кутова швидкість; α - кут повороту вала тахогенератора, описуються рівняннями виду /8.16/.

Перехідна характеристика ланки передставляє собою δ-функцію, тобто імпульс нескінченно великої амплітуди і нескінченно малої ширини. Передаточна функція диференціюючої ланки W(p)=kp. Амплітудно-фазова частотна характеристика і її годограф збігається з додатною уявною піввіссю.

Інерційна ланка

Ця ланка є однією з найпоширеніших ланок систем автоматичного регулювання. Вона описується рівнянням

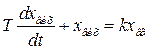, /8.19/

де Т - стала часу, що характеризує швидкість зміни енергії або речовини в ланці; k - коефіцієнт підсилення. Тому що інерційна ланка описується диференційним рівнянням першого порядку, то її також називають ланкою першого порядку.

Рис. 8.7. Інерційна ланка (а) і її амплітудно-фазова частотна характеристика (б).

Прикладами інерційних ланок можуть служити багато об'єктів регулювання, виконавчі пристрої, гідропідсилювачі, електричні кола, що містять індуктивність або ємність, тощо.

Басейн, з якого вода витікає через отвір сталого перерізу, і гідравлічний підсилювач зі зворотним зв'язком описуються рівнянням виду /8.19/. Електричне коло, що складається з індуктивності й опору (рис. 8.7, а), також описується рівнянням /8.19/. Дійсно

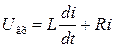. /8.20/

Тому що 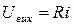, то рівняння /8.20/ зводиться до виду

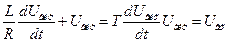. /8.21/

В рівнянні /8.21/ стала часу і коефіцієнт підсилення .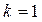

Було показано, що перехідною характеристикою інерційної ланки є експонента.

Передаточна функція інерційної ланки

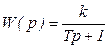. /8.22/

Амплітудно-фазова частотна характеристика

/8.23/

являє собою півколо (рис. 8.7, б). Вона показує, що зі збільшенням ω амплітуда вихідних коливань стосовно вхідних зменшується, а кут зсуву фаз збільшується і при ω =∞ дорівнює —π/2.

Ланка другого порядку

Ця ланка описується диференційним рівнянням другого порядку виду

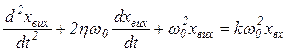, /8.24/

де η - коефіцієнт затухання; ω₀ – частота власних коливань і k - коефіцієнт підсилення.

Рис. 8.8. Ланки другого порядку: а - модель пружної механічної системи; б - електричний коливальний контур і їх амплітудно-фазова частотні характеристики.

Прикладами ланки другого порядку можуть служити пружна механічна система (рис. 8.8, а), електричний коливальний контур (рис. 8.8,б), циліндричний регулятор прямої дії й інші пристрої.

Для пружної механічної системи рівняння сил, що діють на вантаж масою т, відповідно до другого закону Ньютона має вид

, /8.25/

де у - переміщення вантажу; с - коефіцієнт жорсткості пружини; r - коефіцієнт в’язкого тертя демпфера.

Після нескладних перетворень рівняння /8.25/ зводиться до виду

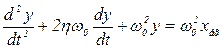, /8.26/

де .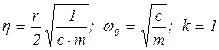

Для коливального контуру відповідно до другого закону Кірхгофа

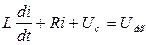, /8.27/

де R - активний опір; L - індуктивність; U_с - спад напруги на конденсаторі.

Оскільки 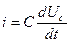, то рівняння /8.27/ зводиться до виду

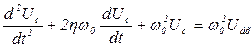, /8.28/

де .

Рівняння /8.24/, /8.26/, /8.28/ одного виду і тому пристрої, що описуються цими рівняннями, є ланками другого порядку.

Перехідна характеристика ланки - це рішення рівняння /8.24/ при 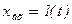. Її вид залежить від коренів характеристичного рівняння

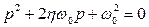. /8.29/

При затуханні η>1 корені рівняння /8.29/ є дійсними від’ємними числами, і

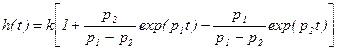, /8.30/

де .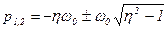

При η<1 корені – комплексно-спряжені з від’ємною дійсною частиною, і

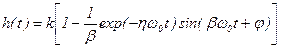, /8.31/

де .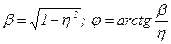

Графіки перехідних характеристик для різних η наведені на рис.8.9. При перехідний процес аперіодичний, а при η<1 - коливально-затухаючий. Тому ланку другого порядку при η<1називають також коливальною ланкою.

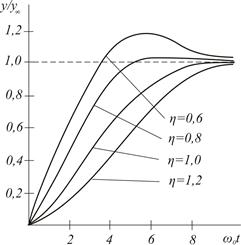
Рис.8.9. Перехідні характеристики ланки другого порядку (а) та її амплітудно-фазові частотні характеристики (б).

Передаточна функція ланки

. /8.32/

Підставивши у вираз /8.32/ 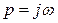, одержують амплітудно-фазову частотну характеристику

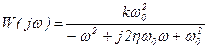. /8.33/

Рівняння /8.33/ показує, що амплітуда вихідних колвань досягає найбільшого значення, рівного , при ω=ω₀, тобто при резонансі. На рис. 8.9.б показані годографи характеристик W(jω) для різних значень η.

Якщо експериментально отриманий годограф W(jω) реальної ланки, близький до ланки другого порядку, то його параметри (k, η і ω₀) знаходять за точками перетину з дійсною і уявною осями.

Ланка зі сталим запізненням

Ця ланка характеризується тим, що відтворює на виході вхідний сигнал без зміни, але ззапізненням на час t.

Запізнення властиве багатьом елементам автоматики, зокрема, поточно-транспортним пристроям, довгим трубопроводам й іншим елементам. Дійсно, якщо за вхідну величину прийняти подачу матеріалу на транспортер, а за вихідну - його появу у кінці транспортера, то час запізнення

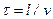, /8.34/

де l - довжина транспортера; ν - швидкість його руху.

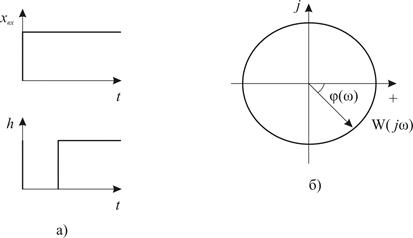
Рис. 8.10. Характеристики ланки зі сталим запізненням: а - перехідна; б - амплітудно-фазова частотна.

Рівняння ланки зі сталим запізненням

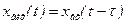, /8.35/

при цьому х_вих=0 для 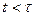. Вираз /8.35/ показує, що вихідна величина повторює вхідну зі зсувом у часі на час .

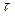Ступінчастий вхідний сигнал і перехідна характеристика h(t) =1(t—τ) показані на рис. 8.10, а.

Передаточна функція ланки

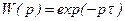. /8.36/

Амплітудно-фазова частотна характеристика 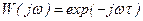являє собою коло радіусом, рівним одиниці, тому що модуль 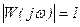(рис.8.10,б). Фаза вихідних коливань пропорційна частоті ω.

З'єднання ланок. Передаточні функції з'єднань

Складні елементи і системи регулювання завжди можна представити у виді певного з'єднання елементарних ланок. З'єднання ланок бувають трьох видів: послідовне, паралельне і з'єднання зі зворотним зв'язком.

Рис. 8.11. Типові з'єднання ланок: а - послідовне; б - паралельне; в - з'єднання зі зворотним зв'язком.

При послідовному з'єднанні ланок вихідна величина однієї ланки є вхідною величиною наступої (рис. 8.11, а). Оскільки у відповідності з визначенням передаточних функцій

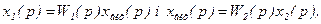то

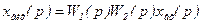. /8.37/

З рівності /8.37/ знаходять передаточну функцію послідовного з'єднання двох ланок:

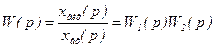. /8.38/

Отже, передаточна функція послідовного з'єднання двох ланок дорівнює добуткові передаточних функцій цих ланок. Даний результат узагальнюється на будь-яке число послідовно з'єднаних ланок.

При паралельному з'єднанні (рис. 8.11,б) на входи всіх ланок подається та сама вхідна величина х_вх, а їхні вихідні величини сумуються (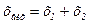). Тому що і , то .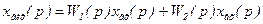

Звідси передаточна функція паралельного з'єднання дорівнює

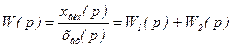. /8.39/

тобто дорівнює сумі передаточних функцій даних ланок. Цей результат також узагальнюється на будь-яке число паралельно з'єднаних ланок.

З'єднання зі зворотним зв'язком, назване також зустрічно-паралельним з'єднанням, утворює замкнутий контур передачі сигналів керування (рис. 8.11, в). Передаточна функція W₁(p) називається передаточною функцією прямого ланцюга передачі сигналів, a W_зз (p) - передаточною функцією зворотного зв'язку.

Якщо вихідний сигнал ланки зворотного зв'язку х_зз співпадає за знаком з вхідним сигналом х_вх, то зворотний зв'язок називається додатним,а якщо протилежний за знаком - то від’ємним.Додатний зворотний зв'язок підсилює дію вхідного сигналу, а від’ємний - послаблює.

При від’ємному зворотному зв'язку

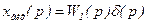; /8.40/

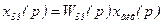; /8.41/

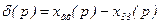. /8.42/

Розв’язавши систему рівнянь /8.40/ — /8.42/, знаходять

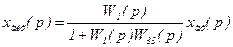. /8.43/

Отже, передаточна функція з'єднання з від’ємним зворотним зв'язком має вигляд

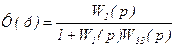. /8.44/

Якщо зворотний зв'язок додатний, то в знаменнику виразу /8.44/ необхідно знак «плюс» поміняти на знак «мінус».

Вирази для передаточних функцій різних видів з'єднань ланок застосовують для знаходження передаточних функцій складних систем регулювання.

Використовуючи рівняння /8.38/ і /8.44/ структурну схему, наведену на рис. 8.12,а, можна звести до з'єднання зі зворотним зв'язком (рис.8.12,б). При цьому

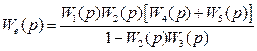, і .

З'єднання зі зворотним зв'язком часто використовують як для зміни параметрів простих елементів, так і для перетворення їхнього виду.

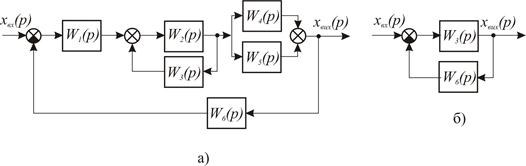
Рис. 8.12. Структурні перетворення: а - вихідна структурна схема; б - перетворена.

Якщо інерційну ланку з передаточною функцією 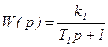охопити від’ємним зворотним зв'язком з передаточною функцією 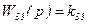, то передаточна функція з'єднання

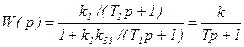, /8.42/

де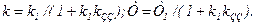

Отже, охоплення інерційної ланки від’ємним зворотним зв’язком зменшує коефіцієнт підсилення і сталу часу в 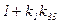раз.

Якщо інтегруючу ланку з передаточною функцією 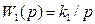охопити від’ємним зворотним зв'язком з W_зз(p)=k_зз,то передаточна функція з'єднання

/8.46/

де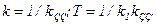

Із /8.46/ видно, що інтегруюча ланка, охоплена від’ємним зворотним зв'язком, перетворюється в інерційну ланку. Розглянуті і подібні види з'єднань простих ланок досить широко використовують для створення систем автоматичного регулювання з бажаними властивостями.

Структурні схеми і характеристики систем автоматичного регулювання

Структурні схеми будують на основі функціональних схем. На рис.8.13 показана функціональна схема системи автоматичного регулювання рівня води в басейні. Вона складається з об'єкта регулювання, циліндричного регулятора і вимірювального пристрою у виді колодязя з поплавком.

Процес регулювання в системі відбувається в такий спосіб. При відхиленні рівня води в басейні від заданого значення, яке контролюється вимірювальним пристроєм у вимірювальному колодязі, пристрій порівняння формує сигнал керування 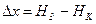, який через регулятор впливає на об'єкт регулювання так, щоб відхилення 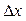зменшувалося.

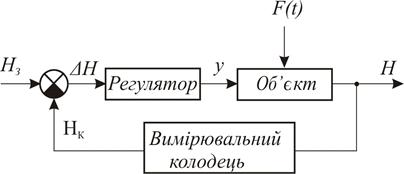
Рис. 8.13. Функціональна схема системи автоматичного регулювання рівня води в басейні.

Вихідна величина Н - рівень води в басейні, є регульованою величиною. Вхідна величина Н₃ називається керуючим впливом або заданим значенням регульованої величини. Вона відтворюється системою регулювання з деякою сталою (статичною) похибкою .

Крім керуючого впливу, на об’єкт керування впливає збурення F(t), що також зумовлює відхилення регульованої величини від заданого значення. Це відхилення називається похибкою регулювання за збуренням і позначається 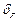. У розглянутій системі основним збуренням є витрата.

Кожен елемент функціональної схеми описується певним рівнянням. Сукупність цих рівнянь описує динаміку системи регулювання. Рівняння елементів розглянутої функціональної схеми можна представити у наступному виді:

елемента порівняння

, /8.47/

де Н_к - рівень води у вимірювальному колодязі;

циліндричного регулятора прямої дії, який представляє собою ланку другого порядку, і як показано в розділі 6 описується рівнянням

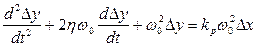; /8.48/

де - переміщення циліндра;

басейну

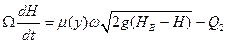, /8.49/

де Ω - площа басейну; μ (у) - коефіцієнт витрати регулятора, що залежить від ступеня його відкриття; ω - площа вихідного перерізу конфузора; Н_в - рівень води у верхньому б'єфі; q₂ - витрата води з басейну;

вимірювального колодязя

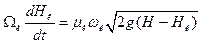/8.50/

де Ω_κ - площа перерізу вимірювального колодязя; μ_κ і ω_к - коефіцієнт витрати вхідного отвору і площа перерізу підвідної труби.

Якщо з рівнянь /8.47/ - /8.50/ послідовно виключити проміжні змінні 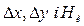, то одержують рівняння, що описує зміну регульованої величини при зміні керуючого впливу. Його називають рівнянням руху системи регулювання. Тому що рівняння /8.49/ і /8.50/ нелінійні, то знайти рівняння руху системи досить складно. З метою спрощення нелінійні рівняння лініаризують, за лінійними рівняннями визначають передаточні функції і складають структурну схему, за допомогою якої легко знаходять рівняння системи.

Для лінеаризації /8.49/ вводять відхилення змінних від їх початкових значень. Позначимо

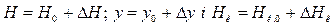. /8.51/

Нелінійну функцію представляємо в виді

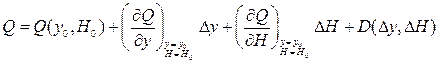, /8.52/

де - нелінійна частина ряду, що містить добутки 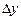і і їх ступені, старші першої.

Тому що згідно /8.65/ 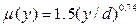, то коефіцієнти степеневого ряду /8.52/

;

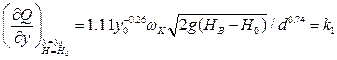Через малі значення відхилень 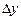і нелінійною частиною ряду можна знехтувати і тим самим замінити нелінійну функцію її лінійним наближенням:

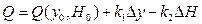. /8.53/

Підставивши вираз /8.53/ у рівняння /8.49/ і з огляду на те, що 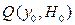дорівнює q_ct, одержимо наступне лініаризоване рівняння об'єкта:

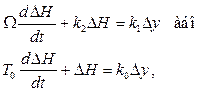/8.54/

де - стала часу об'єкта; 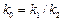- коефіцієнт підсилення об'єкта.

Замінивши в /8.50/ нелінійну функцію 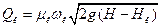двома першими членами степеневого ряду, одержимо

, /8.55/

де 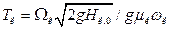- стала часу вимірювального колодязя.

Рівняння /8.55/ є лініаризованим стосовно нелінійного рівняння /8.50/.

Підставивши в /8.48/ і в /8.55/ замість d/dt р і позначивши , одержуємо наступні передаточні функції:

регулятора

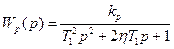; /8.56/

об'єкта регулювання

; /8.57/

вимірювального колодязя

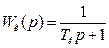. /8.58/

Замінивши у функціональній схемі назви елементів їхніми передаточними функціями, одержимо структурну схему системи регулювання (рис. 8.14, а).

Щоб знайти передаточну функцію системи, структурну схему перетворюють до виду, наведеному на рис. 8.14,б. Оскільки регулятор і об'єкт регулювання з'єднані послідовно, то згідно /8.38/

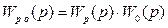. /8.59/

Якщо розірвати зворотний зв'язок у точці а, то система регулювання виявиться розімкненою, і її передаточна функція

/8.60/

називається передаточною функцією розімкненої системи. Ця функція характеризує зв'язок між вихідною величиною вимірювального пристрою і вхідним впливом.

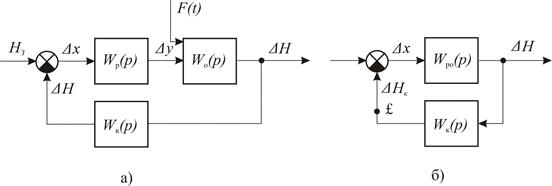
Рис. 8.14. Структурні схеми системи регулювання рівня води в басейні: дійсна (а) і перетворена (б).

Передаточній функції W(p) відповідає рівняння розімкненої системи

/8.62/

де ; ; ; ; .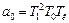

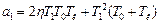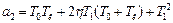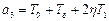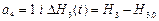З рис. 8.14,б випливає, що замкнена система автоматичного регулювання являє собою з'єднання зі зворотним зв'язком. За формулою /8.44/ передаточна функція замкненої системи

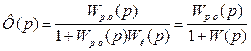. /8.63/

Для системи регулювання води в басейні

. /8.64/

Замінивши в /8.64/ р на одержуємо рівняння руху замкнутої системи регулювання:

/8.65/

Рівняння /8.65/ описує зміну рівня води в басейні при зміні завдання на 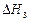. Якщо 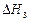- ступінчаста функція, то рішення рівняння /8.65/ являє собою перехідну характеристику замкненої системи. Фізично ступінчастий вхідний вплив - це зміна вхідної величини на .

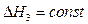В усталеному режимі всі похідні рівні нулю і при /8.65/ приймає вид 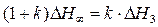, або

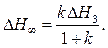. /8.66/

Рівняння /8.66/ встановлює зв'язок між задаючим впливом і регульованою величиною в усталеному режимі і називається рівнянням статики. З /8.66/ випливає, що система відтворює сигнал з похибкою

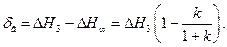/8.67/

З рівняння /8.67/ видно, що для зменшення похибки необхідно збільшувати коефіцієнт підсилення системи k. Якщо задана похибка 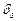, то з /8.67/ можна обчислити необхідне значення коефіцієнта підсилення k.

При виводі рівняння об'єкта регулювання приймали, що витрата води з басейну Q_ст не змінюється. При зменшенні витрати на 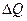і рівняння /8.61/ зводиться до виду

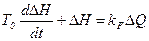, /8.68/

де 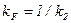- коефіцієнт підсилення об'єкта за збуренням.

Відношення

/8.69/

називається передаточною функцією об'єкта за збуренням.

Відповідно до /8.7/ передаточна функція замкненої системи за збуренням

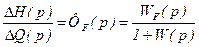. /8.70/

З рівнянь /8.63/ і /8.70/ видно, що передаточні функції Ф(р) і Ф_F(р) відрізняються лише чисельниками. При цьому неважко помітити, що чисельник дорівнює добутку передаточних функції всіх ланок, які знаходяться між точкою прикладення збурення і вихідною величиною. Використовуючи цю закономірність, можна знайти передаточну функцію при дії збурення у будь-якій точці системи. Наприклад, передаточна функція за збуренням , прикладеним до входу регулятора (примусове переміщення поплавка), виразиться залежністю

Для даної системи регулювання передаточна функція за збуренням

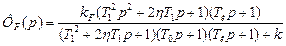. /8.71/

Виразу /8.71/ відповідає диференціальне рівняння

/8.72/

де ; ; .

Рівняння /8.72/ описує перехідний процес, викликаний зменшенням витрати води з басейну. Його рішенням при 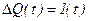є перехідна характеристика системи за збуренням.

Рівняння /8.65/ і /8.72/ мають однакові ліві частини, тому вид і місце прикладення збурення не впливають на коефіцієнти лівої частини рівняння. Останні визначаються параметрами елементів, з яких побудована система.

В усталеному режимі 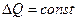і /8.72/ приймає вид:

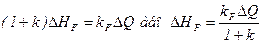. /8.73/

З формули /8.73/ випливає, що відхилення рівня води 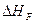в усталеному режимі пропорційно зміні витрати. Зменшити це відхилення можна за рахунок збільшення коефіцієнта підсилення системи k.

Відхилення регульованої величини від заданого значення, зумовлене дією збурення, називається статичною похибкою регулювання за збуренням.У загальному випадку статична похибка за збуренням

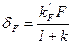, /8.74/

де 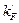- добуток коефіцієнтів підсилення всіх ланок, що знаходяться між точкою прикладання збурення F і вихідною величиною.

Частотні характеристики. Їх широко використовують як при проектуванні, так і при дослідженні властивостей діючих систем. Зокрема, частотні характеристики дозволяють аналізувати відтворення системою гармонійних впливів, досліджувати стійкість, за дійсною частиною амплітудно-частотної характеристики замкненої системи будувати наближену перехідну характеристику й інше. Таке широке застосування частотних характеристик обумовлене тим, що зовнішній вплив довільного виду завжди можна представити сумою гармонійних впливів.

Як уже відзначалося вище, частотні характеристики одержують з передаточних функцій заміною р на .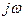

Підставивши в рівняння /8.60/ 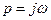, одержують рівняння амплітудно-фазової частотної характеристики розімкненої системи:

. /8.75/

Оскільки 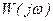дорівнює добуткові частотних характеристик ланок, то за відомими частотними характеристиками ланок легко знайти частотну характеристику 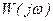, використавши правила множення векторів.

Частотні характеристики замкненої системи одержують з передаточної функції замкненої системи шляхом заміни р на 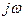. Тому

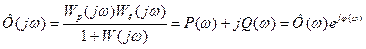, /8.76/

де Ρ (ω) - дійсна; Q(ω) - уявна; Φ (ω) - амплітудна; 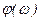- фазова частотні характеристики.

Частотні характеристики замкненої системи дозволяють оцінити властивості системи по каналу «вхід-вихід».

Частотну характеристику

використовують для дослідження реакції системи по каналу «збурення-регульована величина».

Для полегшення побудови амплітудно-фазових частотних характеристик замкнених систем розроблені монограми, що дозволяють за відомою характеристикою 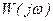визначити характеристики 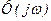або .

Якщо за експериментальними даними побудована характеристика системи 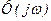, то заміною одержують передаточну функцію, а по ній - рівняння руху системи.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
ХУДОЖНИКИ, ЧИЇ ТВОРИ ЗАКЛАЛИ ОСНОВНІ РИСИ ШВЕЙЦАРСЬКОГО СТИЛЮ.	\|	Поняття та класифікація фінансових ризиків

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.034 сек.