• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Вибір виду рівняння регресії. Регресійний аналіз

У статистичній практиці найбільш поширеними видами рівнянь регресії є такі, параметри яких мають певний фізичний зміст, зокрема:

1. Лінійназалежність 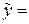а+bх. Параметр а має зміст середнього значення ознаки Y при х=0; якщо ознака Х за своїм фізичним змістом не може приймати нульового значення, то а не має фізичного змісту. Параметр 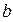має зміст середньої швидкості зміни Y при зміні Х і показує, на скільки одиниць зміниться в середньому значення Y, якщо значення Х зміниться на одиницю.

2. Квадратична залежність 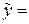р+qx+rx². Параметр р має той же зміст, що і параметр a для лінійного рівняння регресії. Параметр q має зміст середньої початкової швидкості зміни Y при зміні Х. Параметр 2r має зміст середнього прискорення зміни Y при зміні Х і показує, на скільки одиниць в середньому зміниться середня швидкість зміни Y, якщо значення Х зміниться на одиницю.

Існують і інші види рівнянь регресії, які розглядатись не будуть.

Вибір виду рівняння регресії в кожному конкретному дослідженні залежить, в основному, від двох факторів: 1) виду кореляційного поля, яке в даному випадку являє собою сукупність точок з координатами (х_і; у_і) ( ), побудованих в прямокутній системі координат хоу; 2) ретельного вивчення суті явища, що досліджується, з урахуванням результатів попередніх аналогічних досліджень, якщо останні проводились.

Можлива ситуація, коли ні аналіз явища, ні вигляд кореляційного поля не дають можливості однозначно вибрати вид рівняння регресії. В такому випадку необхідно вибрати дві (або більше) найбільш адекватні на погляд дослідника функції f(x), провести для кожної повне дослідження і за їх результатами вибрати одну, кращу. При цьому можна формалізувати вибір, обираючи, наприклад, ту залежність, для якої регресійна дисперсія (3.11) буде меншою за інші або використовувати існуючі критерії адекватності моделі експериментальним даним.

Зауважимо, що остаточний вибір рівняння регресії, іноді суб’єктивний, залишається все-таки за дослідником.

Читайте також:

1. ABC-XYZ аналіз
2. I етап. Аналіз впливу типів ринку на цінову політику.
3. I. Аналіз контрольної роботи.
4. II. Багатофакторний дискримінантний аналіз.
5. III етап. Аналіз факторів, що визначають цінову політику підприємства.
6. III. Аналіз ринку
7. IV Етап: Вибір стратегії керування виявленими ризиками й виділення пріоритетних напрямків роботи
8. IV розділ. Сегментація ринку та вибір цільового сегменту
9. IV. ВИБІР КОНТРОЛЬНИХ ЗАВДАНЬ ТА ВИМОГИ ДО НАПИСАННЯ КОНТРОЛЬНИХ РОБІТ
10. IІI розділ. Аналіз стану маркетингового середовища підприємства
11. SWOT-аналіз у туризмі
12. SWOT-аналіз.

Переглядів: 1062