
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Приклади розкриття статичної невизначуваності
Приклад 1
Дано:  .
.
Визначити: Для шарнірно обпертої балки, навантаженої силою F, побудувати епюри згинального моменту і поперечної сили.
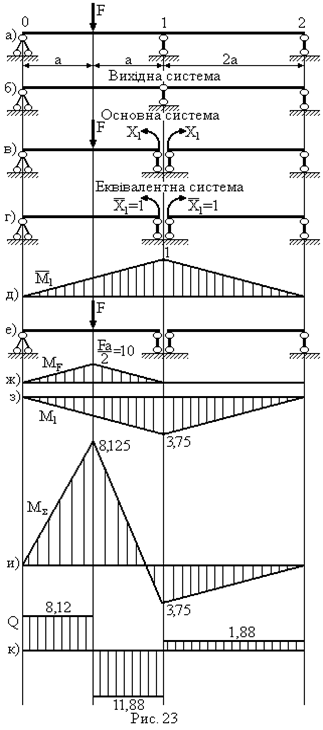
|
- Визначається ступінь статичної невизначуваності балки (рис. 23а):  .
.
Нумерацію опор рекомендовано починати з нульової.
- Горизонтальна реакція в шарнірно – нерухомій опорі 0 буде рівною нулю, тому що немає сил, які дають ненульову проекцію на вісь балки.
- Обираємо основну статично визначувану систему (рис. 23б). Для цього встановимо додатковий шарнір в тіло балки над проміжною (середньою) опорою. При цьому згинальний момент в даному перерізі перетворюється на нуль. Балка розпадається на дві незалежні прості балки.
- Формуємо еквівалентну систему шляхом прикладання зовнішньої сили 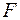 і невідомого згинального моменту
і невідомого згинального моменту 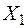 в перерізі з одиночним шарніром (рис. 23в).
в перерізі з одиночним шарніром (рис. 23в).
- До основної системи прикладаємо одиничний момент 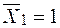 (рис. 23г) і будуємо епюру
(рис. 23г) і будуємо епюру  (рис. 23д).
(рис. 23д).
- До основної системи прикладаємо зовнішнє навантаження (силу 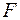 ) (рис.23е) і будуємо епюру
) (рис.23е) і будуємо епюру  (рис. 23ж).
(рис. 23ж).
- Записуємо канонічне рівняння метода сил:  . Тут
. Тут 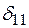 – взаємний кут повороту в місці встановлення додаткового шарніра від прикладання одиничного згинального моменту в напрямку його дії, а
– взаємний кут повороту в місці встановлення додаткового шарніра від прикладання одиничного згинального моменту в напрямку його дії, а 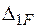 – взаємний кут повороту в місці встановлення одиничного шарніра від прикладання зовнішнього навантаження (сили
– взаємний кут повороту в місці встановлення одиничного шарніра від прикладання зовнішнього навантаження (сили 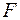 ).
).
- Визначаємо коефіцієнти канонічного рівняння метода сил:
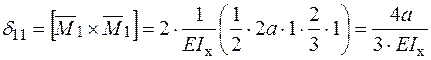
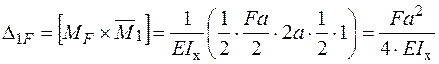 .
.
- Розв’язуємо канонічне рівняння і визначаємо 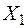 :
:
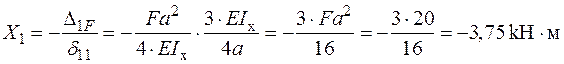 .
.
- Будуємо епюру 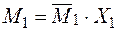 від знайденого моменту
від знайденого моменту 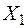 (рис. 23з).
(рис. 23з).
- Шляхом складання по ділянках балки епюри  (рис. 23ж) і епюри
(рис. 23ж) і епюри 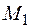 (рис. 23з) будуємо епюру
(рис. 23з) будуємо епюру 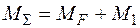 (рис. 23и).
(рис. 23и).
- Перевірка виконання умови еквівалентності проводиться шляхом визначення взаємного кута повороту в місці одиночного шарніра. Якщо цей взаємний кут повороту з заданою точністю (3¸5%) буде дорівнювати нулю, то розрахунки по розкриттю статичної невизначуваності та побудови епюри  вірні. Для цього необхідно перемножити епюру згинальних моментів
вірні. Для цього необхідно перемножити епюру згинальних моментів  (рис. 23и) для статично невизначуваної системи і епюру згинальних моментів
(рис. 23и) для статично невизначуваної системи і епюру згинальних моментів  (рис. 23з) від одиничного навантаження, прикладеного в місці встановлення одиночного шарніра:
(рис. 23з) від одиничного навантаження, прикладеного в місці встановлення одиночного шарніра:

- Епюра поперечних сил 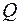 (рис. 23к) будується з урахуванням опорних реакцій, які визначаються для еквівалентної системи (рис. 23в) після знаходження моменту
(рис. 23к) будується з урахуванням опорних реакцій, які визначаються для еквівалентної системи (рис. 23в) після знаходження моменту 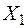 .
.
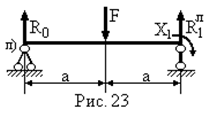
| Для ділянки балки 0-1:
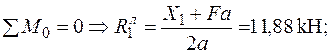
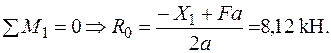
|

| Для ділянки балки 1-2:
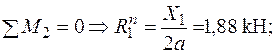
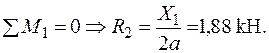
|
При цьому, для ділянок балки 0-1 та 1-2 опорні реакції знаходяться окремо, а сумарна реакція у першому шарнірі визначається за алгебраїчною сумою лівої і правої частки цієї реакції:
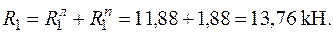
Приклад 2

| Дано:
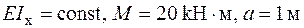 .
Визначити: Для прямокутної рами (рис.24), навантаженої моментом М, побудувати епюри згинального моменту, поздовжніх та поперечних сил. .
Визначити: Для прямокутної рами (рис.24), навантаженої моментом М, побудувати епюри згинального моменту, поздовжніх та поперечних сил.
|
Визначається ступінь статичної невизначуваності балки (рис. 24):  .
.
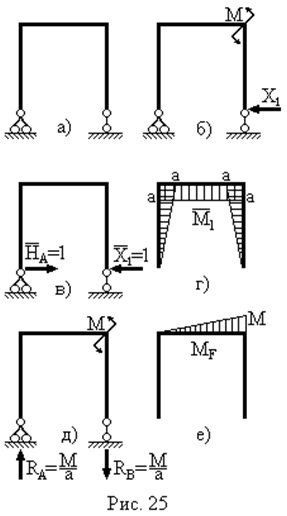
| Обираємо основну статично визначувану систему (рис. 25а). Для цього встановимо рухомий шарнір замість нерухомого в точці В.
Формуємо еквівалентну систему шляхом прикладання зовнішнього моменту М і невідомої сили 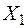 у точці В в напрямку (горизонтальному) відкинутого зв’язку (рис. 25б).
До основної системи прикладаємо одиничний момент у точці В в напрямку (горизонтальному) відкинутого зв’язку (рис. 25б).
До основної системи прикладаємо одиничний момент 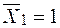 (рис. 25в) і будуємо епюру (рис. 25в) і будуємо епюру  (рис. 25г). (рис. 25г).
|
До основної системи прикладаємо зовнішнє навантаження (момент М) (рис.25д) і будуємо епюру  (рис. 25е).
(рис. 25е).
Записуємо канонічне рівняння метода сил:  . Тут
. Тут 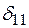 – лінійне переміщення у точці В в напрямку сили
– лінійне переміщення у точці В в напрямку сили 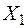 від одиничної сили
від одиничної сили 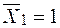 , а
, а 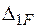 – лінійне переміщення у точці В в напрямку сили
– лінійне переміщення у точці В в напрямку сили 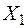 від прикладання зовнішнього навантаження (моменту М).
від прикладання зовнішнього навантаження (моменту М).
Визначаємо коефіцієнти канонічного рівняння метода сил:

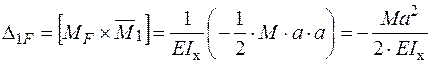 .
.
Розв’язуємо канонічне рівняння і визначаємо 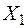 :
:
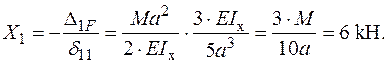

| 
|
Будуємо епюру 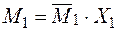 від знайденої сили
від знайденої сили 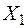 (рис. 26а).
(рис. 26а).
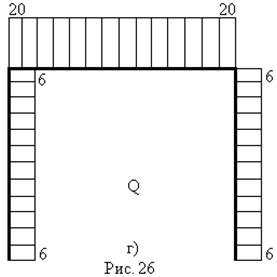
Шляхом складання по ділянках балки епюри  (рис. 25е) і епюри
(рис. 25е) і епюри 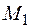 (рис. 25г) будуємо епюру
(рис. 25г) будуємо епюру 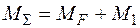 (рис. 26б).
(рис. 26б).
Для один раз статично невизначеної системи перевірка виконання умови еквівалентності, а таким чином правильності розрахунків по розкриттю статичної невизначуваності та побудови епюри  , проводиться визначенням лінійного переміщення
, проводиться визначенням лінійного переміщення 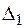 в напрямку
в напрямку 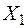 . Горизонтальне переміщення
. Горизонтальне переміщення 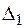 з заданою точністю
з заданою точністю 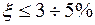 повинно дорівнювати нулю. Для цього необхідно перемножити епюру згинальних моментів
повинно дорівнювати нулю. Для цього необхідно перемножити епюру згинальних моментів  (рис. 26б) для статично невизначуваної системи і епюру згинальних моментів
(рис. 26б) для статично невизначуваної системи і епюру згинальних моментів  (рис. 25г) г) від одиничного навантаження
(рис. 25г) г) від одиничного навантаження 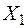 :
:
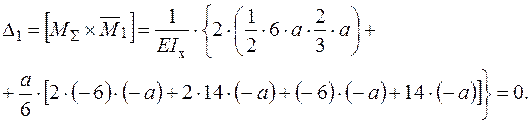
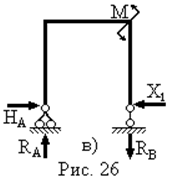
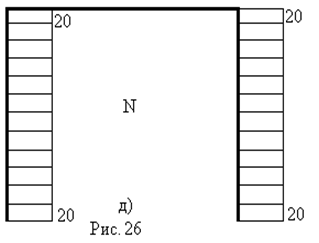
Епюри поздовжніх – 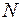 та поперечних –
та поперечних – 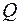 сил (рис. 26г,д) будуються з урахуванням опорних реакцій в шарнірах А і В, які визначаються для еквівалентної системи (рис. 25б) після знаходження сили
сил (рис. 26г,д) будуються з урахуванням опорних реакцій в шарнірах А і В, які визначаються для еквівалентної системи (рис. 25б) після знаходження сили 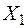 .
.
| 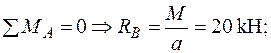
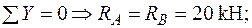
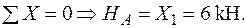
|
|
|
Приклад 3

| Дано: 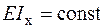 .
Визначити: Для плоскої рами (рис.27), навантаженої силою .
Визначити: Для плоскої рами (рис.27), навантаженої силою 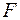 посередині лівого стояка розкрити статичну невизначуваність і побудувати епюри внутрішніх силових факторів в загальному випадку. посередині лівого стояка розкрити статичну невизначуваність і побудувати епюри внутрішніх силових факторів в загальному випадку.
|
Ступінь статичної невизначуваності для даної рами дорівнює:  .
.
Для утворення основної системи зробимо розріз по площині симетрії, а зовнішнє навантаження приведемо до симетричного і кососиметричного (рис.28а,в).
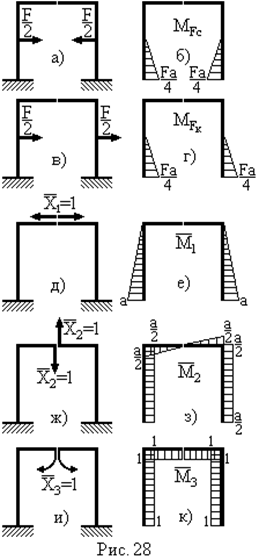
| Для визначення зайвих невідомих зусиль скористаємося канонічними рівняннями:
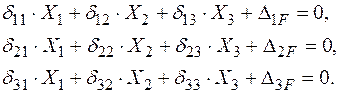 У цих рівняннях переміщення
У цих рівняннях переміщення  та та 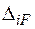 є відповідними переміщеннями сторін розрізу.
Задача розв’язується в два етапи:
- для симетричного прикладання сил є відповідними переміщеннями сторін розрізу.
Задача розв’язується в два етапи:
- для симетричного прикладання сил 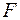 (рис.28а). Епюра згинального моменту (рис.28а). Епюра згинального моменту 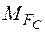 (рис.28б).
- для кососиметричного прикладання сил (рис.28б).
- для кососиметричного прикладання сил 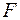 (рис.28в). Епюра згинального моменту (рис.28в). Епюра згинального моменту 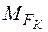 (рис.28г). (рис.28г).
|
Епюри згинальних моментів 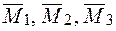 будуються для схем навантаження (рис. 28д,ж,и), відповідно (рис. 28е,з,к).
будуються для схем навантаження (рис. 28д,ж,и), відповідно (рис. 28е,з,к).
Зазначимо, що епюри  – симетричні,
– симетричні, 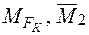 – кососиметричні.
– кососиметричні.
Визначимо коефіцієнти канонічних рівнянь для симетричного прикладання сили 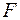 .
.

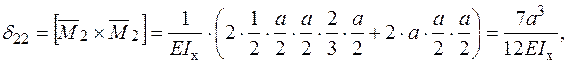
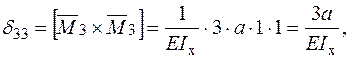
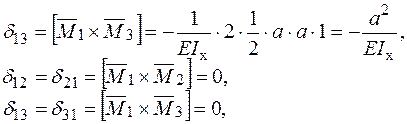

Підставляємо коефіцієнти в канонічні рівняння і розв’язуючи систему алгебраїчних рівнянь знаходимо внутрішні силові фактори для симетричного прикладання сили.
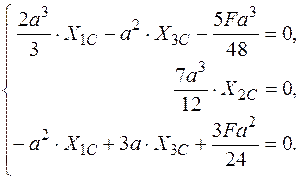 Þ
Þ
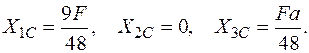
Визначимо коефіцієнти канонічних рівнянь для кососиметричного прикладання сили 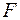 . Коефіцієнти від одиничних навантажень залишаються без змін.
. Коефіцієнти від одиничних навантажень залишаються без змін.

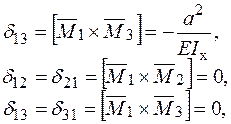

Підставляємо коефіцієнти в канонічні рівняння і розв’язуючи систему алгебраїчних рівнянь знаходимо внутрішні силові фактори для кососиметричного прикладання сили.
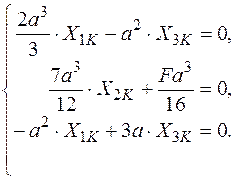 Þ
Þ
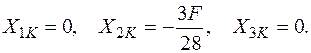
Знаходимо внутрішні силові фактори для заданого навантаження.
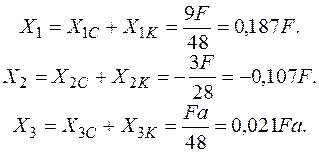
Будуємо епюри  .
.

|
Для тричі статично невизначеної системи перевірка виконання умови еквівалентності, а таким чином правильності розрахунків по розкриттю статичної невизначуваності та побудови епюри  , проводиться в три етапи. На першому етапі визначається лінійне переміщення
, проводиться в три етапи. На першому етапі визначається лінійне переміщення 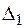 в напрямку
в напрямку 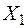 . Взаємне горизонтальне переміщення на осі симетрії з заданою точністю
. Взаємне горизонтальне переміщення на осі симетрії з заданою точністю 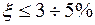 повинно дорівнювати нулю. Для цього необхідно перемножити епюру згинальних моментів
повинно дорівнювати нулю. Для цього необхідно перемножити епюру згинальних моментів  для статично невизначуваної системи і епюру згинальних моментів
для статично невизначуваної системи і епюру згинальних моментів  від одиничного навантаження
від одиничного навантаження 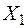 .
.


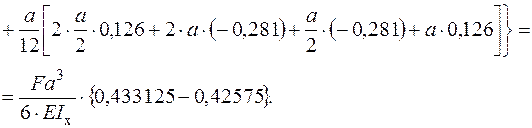

На другому етапі визначається лінійне переміщення 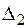 в напрямку
в напрямку  . Взаємне вертикальне переміщення на осі симетрії з заданою точністю
. Взаємне вертикальне переміщення на осі симетрії з заданою точністю 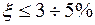 повинно дорівнювати нулю. Для цього необхідно перемножити епюру згинальних моментів
повинно дорівнювати нулю. Для цього необхідно перемножити епюру згинальних моментів  для статично невизначуваної системи і епюру згинальних моментів
для статично невизначуваної системи і епюру згинальних моментів 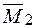 від одиничного навантаження
від одиничного навантаження  .
.
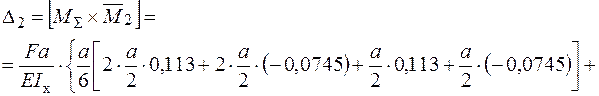
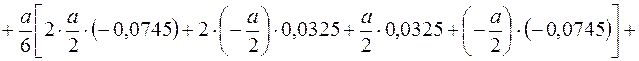


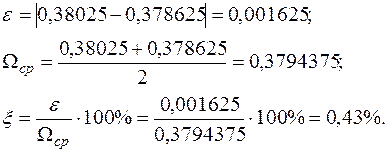
На третьому етапі визначається кутове переміщення  в напрямку
в напрямку 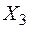 . Взаємний кут повороту на осі симетрії з заданою точністю
. Взаємний кут повороту на осі симетрії з заданою точністю 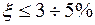 повинен дорівнювати нулю. Для цього необхідно перемножити епюру згинальних моментів
повинен дорівнювати нулю. Для цього необхідно перемножити епюру згинальних моментів  для статично невизначуваної системи і епюру згинальних моментів
для статично невизначуваної системи і епюру згинальних моментів 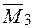 від одиничного навантаження
від одиничного навантаження 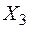 .
.
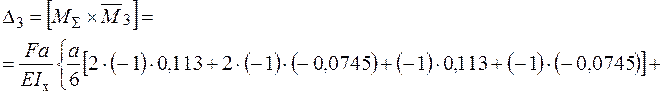
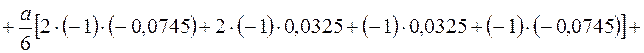
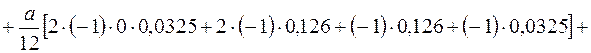
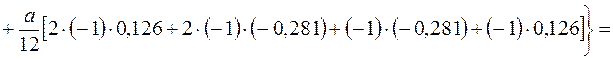
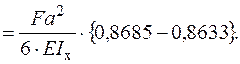
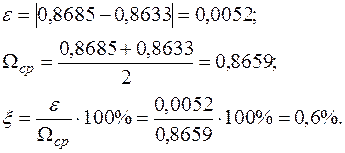
Читайте також:
- IV. ПРИКЛАДИ ТИПОВИХ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ ТА ПОРЯДОК ЇХ РОЗВ’ЯЗАННЯ
- Аналітичний і синтетичний облік власного капіталу та розкриття інформації у фінансовій звітності
- Буріння свердловин і розкриття продуктивних пластів з допомогою промивних рідин із органоколоїдними складовими
- В процесі читання виділіть маркером або підкресліть приклади дії променів на живі організми.
- В чому полягає явище тунелювання через потенціальний бар’єр, наведіть приклади.
- Вибір промивної рідини для розкриття пласта
- Визначення і приклади
- Виконання спеціального завдання з попередження чи розкриття злочинної діяльності організованої групи або злочинної організації
- Виконання спеціального завдання з попередження чи розкриття злочинної діяльності організованої групи чи злочинної організації.
- Виокремте з обраної програми концептуальну ідею, мету, наведіть 1-2 приклади форм і методів її реалізації.
- Виховна мета:сприяти формуванню професійних якостей спеціаліста правоохоронної сфери діяльності з розкриття та розслідування злочинів.
- Виявлення та розкриття легалізації (відмивання) доходів, одержаних злочинним шляхом
| <== попередня сторінка | | | наступна сторінка ==> |
| Перевірка правильності розрахунків | | | Розрахунково – проектувальне завдання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |