
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Теоретичні відомості
Лабораторна робота №2
Операції над нечіткими множинами
Ціль:вивчити операції над нечіткими множинами.
Теоретичні відомості
Операції над нечіткими множинами узагальнюють операції над звичайними множинами. Ці операції звичайно виконуються поелементно над значеннями функції належності (ФН). Найбільш популярні операції перетинання й об'єднання нечітких множин, обумовлені, відповідно, операціями знаходження мінімуму і максимуму над значеннями належності. Порівняння нечітких множин і виконання над ними різних операцій стає можливим, якщо відповідні нечіткі множини визначені на тому самому универсумі [5].
Насамперед, розглянемо два найпростіших звичайних відношення, які можуть мати місце між двома довільними нечіткими множинами А и В, заданими на тому самому универсумі Х [1].
1.Рівність нечітких множин
Дві нечітких множини A={x,µA(x)} і B={x,µB(x)} вважаються рівними, якщо їх функції належності приймають рівні значення на всім универсумі Х:
 (2.1)
(2.1)
Рівність у цьому випадку записується як А=В.
2.Включення (вміст)
Нечітка множина A={x,µA(x)} є нечіткою підмножиною нечіткої множини B={x,µB(x)} тоді, коли значення функції належності першої не перевершують відповідних значень функції приналежності другої, тобто виконується наступна умова:
 (2.2)
(2.2)
Далі розглянемо операції над нечіткими множинами, що зустрічаються найчастіше.
1.Перетинання (Кон’юнкція, «І»)
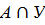 – найбільша нечітка підмножина, що міститься одночасно в A і B:
– найбільша нечітка підмножина, що міститься одночасно в A і B:
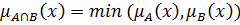 (2.3)
(2.3)
Нехай А – нечіткий інтервал між 5 і 8, В – нечітке число наближене до 4, як показано на рисунку 2.1.

Рис. 2.1 Нечіткі множини А и В
Проілюструємо на рисунку 2.2 операцію перетинання 2х нечітких множин.

Рис. 2.2 Операція перетинання A AND B
Приклад 2.1.
 (2.4)
(2.4)
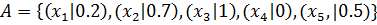 (2.5)
(2.5)
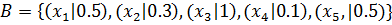 (2.6)
(2.6)
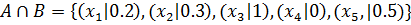 (2.7)
(2.7)
2.Об'єднання (Диз'юнкція, «АБО»)
 – найменша нечітка підмножина, що включає як А, так і В:
– найменша нечітка підмножина, що включає як А, так і В:
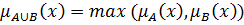 (2.8)
(2.8)
Проілюструємо на рисунку 2.3 операцію об'єднання 2х нечітких множин А и В, представлених на рисунку 2.1.

Рис. 2.3 Операція об'єднання A OR B
Приклад 2.2.
 (2.9)
(2.9)
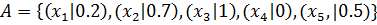 (2.10)
(2.10)
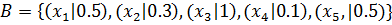 (2.11)
(2.11)
 (2.12)
(2.12)
3.Доповнення (логічне заперечення)
Доповнення нечіткої множини є не що інше, як математичне подання вербального вираження «НЕ А», де А – нечітка множина, що описує деяке розмите судження.
Нехай Е – множина, M = [0,1], A і B – нечіткі множини, задані на E. A і B доповнюють один одного, якщо:
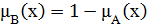 (2.12)
(2.12)
Це можна позначити так:
 (2.13)
(2.13)
Рисунок 2.4 ілюструє операцію заперечення нечіткої множини А.

Рис. 2.4 Операція заперечення нечіткої множини A
Приклад 2.3.
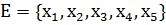 (2.14)
(2.14)
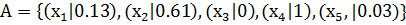 (2.15)
(2.15)
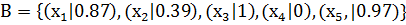 (2.16)
(2.16)
Тоді очевидно, що
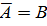 (2.17)
(2.17)
4.Добутком нечітких множин A і B називається нечітка підмножина з функцією належності [2]:
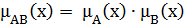 (2.18)
(2.18)
5.Сумою нечітких множин A і B називається нечітка підмножина з функцією належності:
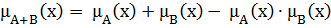 (2.19)
(2.19)
6.Різниця нечітких множин A і B визначається співвідношенням:
 (2.20)
(2.20)
7.Відстань Хеммінга, або лінійна відстань, визначається за формулою:
 (2.21)
(2.21)
8.Євклідова відстань або квадратична відстань, визначається за формулою:
 (2.22)
(2.22)
У середовищі Matlabіснує можливість визначати кон’юнктивні та диз’юнктивні оператори з точки зору мінімаксної и ймовірностної інтерпретації.
Розглянемо мінімаксну інтерпретацію логічних операторів, в котрій кон’юнктивний оператор представляє знаходження мінімуму – min, а диз’юнктивний – максимум – max.
Опис кон’юнктивної функції: у = min ([у1; у2]).
Опис диз’юнктивної функції: у = тах ([у1; у2]).
Параметри у1 и у2 являють собою початкові функції належності. Функція min працює зі списком ФН. В Matlab список оформлюється квадратними скобками, а елементи списку розділяються крапкою з комою [3].
Читайте також:
- D - порушення стану свідомості (Disability).
- II.ТЕОРЕТИЧНІ ПИТАННЯ КУРСОВОЇ РОБОТИ
- IX. Відомості про військовий облік
- IX. Відомості про військовий облік
- L. Ефективність праці: теоретичні аспекти
- Q Конституція України від 28 червня 1996 р. // Відомості Верховної Ради України – 1996 - № 30 – Ст. 141
- V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
- Активне управління інвестиційним портфелем - теоретичні основи.
- Білковий обмін: загальні відомості
- Біографічні відомості
- Боротьба з проявами національної самосвідомості
- Вальниці ковзання. Загальні відомості
| <== попередня сторінка | | | наступна сторінка ==> |
| Вимоги до оформлення звітів по лабораторних роботах | | | Приклад 2.4. Програма використання операцій min и max |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |