• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Одна ланка охоплюється у вигляді зворотного зв’язку другою ланкою

Зворотний зв’язок може бути додатний та від’ємний. При з’єднанні ланки 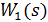, охопленої у вигляді зворотного зв’язку другою ланкою 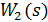(рис. 5,в), мають місце наступні співвідношення:

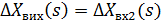
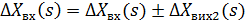
Передавальні функції ланок та всього з’єднання запишуться у вигляді:

;

;

.

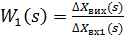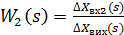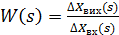Визначимо передавальну функцію з’єднання :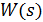

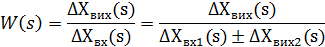
Поділимо чисельник та знаменник на :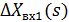

Отже отримаємо:

,

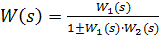де знак “+” відповідає від’ємному, а “-”додатному зворотному зв’язку.

Якщо у зворотному зв’язку відсутня ланка, тобто має місце одиничний зворотний зв’язок 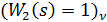то

.

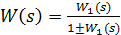Отримані вирази передавальних функцій типових з’єднань ланок дозволяють спростити складну структурну схему системи і тим самим полегшити визначення передавальної функції системи.

Задача №1. Знайти передаточну функцію замкнутої системи. Система складається з: об’єкта – аперіодичної ланки, та регулятора – інтегруючої ланки. Система замкнута, працює за відхиленням.

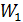
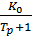
Рис.6 Структурна схема

Знайдемо передаточну функцію розімкнутої системи:

;

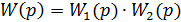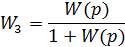
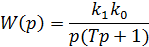
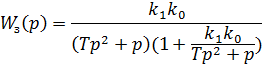
Задача №2. Знайти вираз для передаточної функції замкнутої системи, якщо передаточна функція розімкнутої системи має вигляд: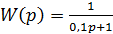

X Y

W(p)

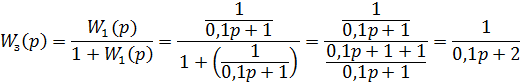
Задача №3. Знайти еквівалентну передаточну функцію паралельного узгодженого з’єднання двох ланок, якщо їх передаточні функції відповідно рівні: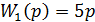

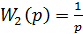
x y

.

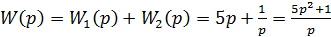Задача №4. Спростити складну структурну схему системи і тим самим полегшити знаходження передаточної функції.

.

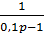
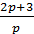
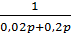
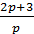
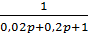
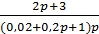
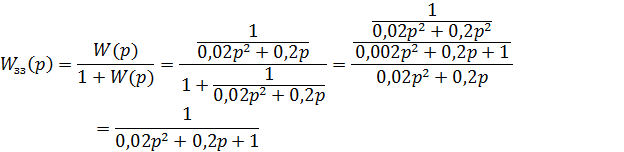
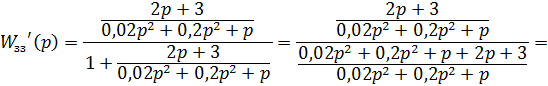
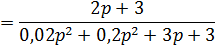
Читайте також:

1. А) Поліпшення системи зворотного зв'язку.
2. А) Поліпшення системи зворотного зв’язку.
3. Аналіз взаємозв’язку собівартості, обсягів і прибутку
4. Антиконкурентна поведінка у вигляді зловживання монопольним становищем
5. Біологічна регуляція, її види і значення. Контур біологічної регуляції. Роль зворотнього зв’язку в регуляції.
6. В-88 Квантування електронних орбіт і виникнення хімічного зв’язку в твердих тілах
7. Взаємовідносини між ланками бюджетної системи
8. Визначення тісноти взаємозв’язку між рівнем комплексного коефіцієнта комфортабельності судна та добовою тарифною ставкою круїзу
9. Визначити хто платить ПДВ, якщо підприємство вносить вклад до статуного фонду у вигляді основних засобів на суму 7000 грн.
10. Виконавчою владою охоплюється найширша сфера відносин у державі.
11. Виконання рішень щодо покарання у вигляді штрафу та конфіскації майна.
12. Використання ОЗК у вигляді комбінезону

Переглядів: 835