
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Визначення тісноти взаємозв’язку між рівнем комплексного коефіцієнта комфортабельності судна та добовою тарифною ставкою круїзу
Вводиться гіпотеза, що між фактором х та показником y існує лінійна стохастична залежність вигляду 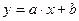 .
.
Оцінки параметрів а і b парної регресії обчислюються за формулами:
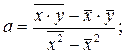
| (2.1) |

| (2.2) |
Розрахуємо коефіцієнт кореляції:
 , ,
| (2.3) |
де  - середнє квадратичне відхилення ознаки х;
- середнє квадратичне відхилення ознаки х;
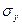 - середнє квадратичне відхилення ознаки у.
- середнє квадратичне відхилення ознаки у.
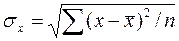
| (2.4) |

| (2.5) |
Коефіцієнт кореляції є відносною мірою зв'язку між двома ознаками, тому він може набувати значення від -1 до +1. Чим ближче значення rху до ±1, тим щільніший зв'язок. Знак "+" вказує на прямий, а знак "-" - на зворотний зв'язок. При rху = 0 зв'язок відсутній.
Поряд з коефіцієнтом кореляції використовується ще один критерій, за допомогою якого також вимірюється щільність зв'язку між двома або більше показниками та перевіряється адекватність (відповідність) побудованої регресійної моделі реальній дійсності. Тобто дається відповідь на запитання, чи дійсно зміна значення у лінійно залежить саме від зміни значення х, а не відбувається під впливом різних випадкових факторів. Таким критерієм є коефіцієнт детермінації.
Визначимо коефіцієнт детермінації:

| (2.6) |
Коефіцієнт детермінації завжди позитивний і перебуває в межах від нуля до одиниці. Він показує, яка частка коливань результативної ознаки y зумовлена коливанням факторної ознаки х.
Для оцінки адекватності прийнятої економетричної моделі експериментальним даним використовуємо критерій Фішера. Для цього порівнюють розрахункове значення критерію Фішера із табличним. Перевіримо гіпотезу 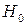 про статистичну незначність рівняння регресії
про статистичну незначність рівняння регресії 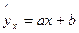 .
.
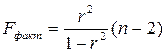
| (2.7) |
Табличне значення критерію Фішера обчислюють наступним чином:
- визначають k1, яке дорівнює числу факторів (Х). Наприклад, в однофакторній моделі (моделі парної регресії) k1=1, в двохфакторній – k1 = 2;
- визначають k2 по формулі n - m - 1, де n - число спостережень, m - кількість факторів. Наприклад, в одно факторній моделі k2 = n – 2;
- на перетині стовбця k1 и строки k2 знаходять величину крітерія Фішера.
Для оцінки статистичної значущості моделі за параметрами використовується t-критерій Ст’юдента.
Оцінка значущості моделі за допомогою критерію Ст’юдента виконується шляхом порівняння їх значень з величиною випадкової помилки:
| tb = b/mb | (2.8) |
| ta = a/ma | (2.9) |
| tr = r/mr | (2.10) |
Випадкові помилки коефіцієнтів лінійної регресії і коефіцієнта кореляції визначаються за формулами:
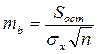
| (2.11) |

| (2.12) |

| (2.13) |
mrxy = 
| (2.14) |
Порівнюючи фактичне і табличне значення t-статистики приймається або відхиляється гіпотеза о значущості моделі за параметрами.
Залежність між критерієм Фішера і значеннямt-статистики Ст׳юдента визначається так:
 
| (2.15) |
Для визначення табличної величини критерію Ст׳юдента знаходять число ступенів свободи (2.16) при визначеному рівні значущості 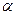 (0,10, 0,05, 0,01).
(0,10, 0,05, 0,01).
| d.f. = n - m – 1 | (2.16) |
Як і в випадку з оцінкою значущості рівняння моделі в цілому, модель вважається надійною, якщо tтабл > tфакт.
Для побудови довірчих інтервалів визначається гранична помилка Δ для обох показників:
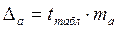
| (2.17) |
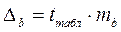
| (2.18) |
Формули для находження довірчих інтервалівмають такий вигляд:
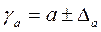
| (2.19) |
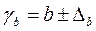
| (2.20) |
Розрахуємо надійні зони базисних даних для кожного показника y:
Ø середня стандартна помилка
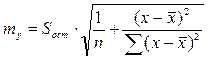 ; ;
| (2.21) |
Ø гранична помилка
 ; ;
| (2.22) |
Ø надійний інтервал
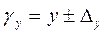
| (2.23) |
Прогнозне значення у визначається за допомогою підстановки в рівняння регресії прогнозного значення х. Визначається середня стандартна помилка прогнозу(2.21) і знаходиться довірчий інтервал (2.23):
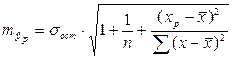
| (2.24) |

| (2.25) |
 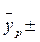 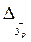
| (2.26) | ||
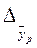 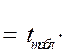 
| (2.27) | ||
Коефіцієнт еластичності – це коефіцієнт, який характеризує відносну зміну одного признаку при одиничній відносній зміні іншого.
Коефіцієнт еластичності для базисних даних та прогнозу обчислюється за формулою.
| Кел = а*х / ỹ | (2.28) |
Результати розрахунків представляються у вигляді табл. 2.2.
Таблиця 2.2
| Номер | Кк(х) | f (у) | ху | Х2 | (x-хс)2 | (y-ус)2 | ỹ | (y-yr)2 | mу | Δy | 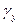 (min) (min)
| 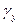 (max) (max)
| Kел |
| 1 | |||||||||||||
| 2 | |||||||||||||
| … | |||||||||||||
| 16 | |||||||||||||
| Прогноз | |||||||||||||
| Всего | |||||||||||||
| Среднее |
Для зручності розрахунків і перевірки їхніх результатів вхідні дані, отримані на попередніх етапах проектування, необхідно вносити в табл. 2.2.
У випадку якщо розрахунки проводяться з використанням програми електронних таблиць ЕХЕL, то таблиці на робочому аркуші ЕХЕL також рекомендується оформляти у вигляді табл. 2.2.
Для наочного уявлення одержаних розрахунків на окремому листі будуємо графіки фактичних даних (y), лінії регресії для базисних даних та прогнозу, довірчі інтервали для базисних даних і прогнозу. Коефіцієнт еластичності – на окремому графіку.
Примітка: звернути увагу на фактор х, якщо дані не відсортовані, то передусім відсортувати їх разом з усіма відповідними стовпчиками на окремому листі.
Читайте також:
- CMM. Визначення моделі зрілості.
- I визначення впливу окремих факторів
- I підготовка їх до завантаження у повітряні судна
- II. Визначення мети запровадження конкретної ВЕЗ з урахуванням її виду.
- II. Мотивація навчальної діяльності. Визначення теми і мети уроку
- Ocнoвнi визначення здоров'я
- S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
- А. Визначення розмірів і площі зони хімічного зараження.
- Агресивний тип дивідендної політики включає метод стабільного приросту дивідендів і метод постійного коефіцієнта виплат.
- Акустичні рівнеміри
- Алгебраїчний спосіб визначення точки беззбитковості
- Алгоритм визначення проекцій точок на поверхнях обертання
| <== попередня сторінка | | | наступна сторінка ==> |
| Розділ 2. | | | Аналіз отриманих результатів |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |