Геометричні ймовірності

Щоб перебороти недолік класичного визначення ймовірності, який полягає в тому, що воно незастосовне до випробувань з нескінченним числом результатів, вводять геометричні ймовірності - ймовірності попадання точки в область (відрізок, частину площини тощо).

Нехай відрізок 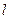складає частину відрізка 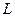. На відрізок L навмання поставлена точка. Це означає виконання наступних припущень: поставлена точка може виявитися в будь-якій точці відрізка L, ймовірність попадання точки на відрізок 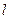пропорційна довжині цього відрізка і не залежить від його розташування щодо відрізка L. У цих припущеннях ймовірність попадання точки на відрізок 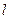визначається рівністю

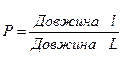Приклад 1. На відрізок ОА довжини L числової осі Ох навмання поставлена точка В(х). Знайти ймовірність того, що менший з відрізків ОВ і ВА має довжину, більшу L/3. Передбачається, що ймовірність попадання точки на відрізок пропорційна довжині відрізка і не залежить від його розташування на числовій осі.

Рішення. Розіб’ємо відрізок ОА точками С і D на 3 рівні частини. Вимога задачі буде виконана, якщо точка В(х) потрапить на відрізок CD довжини 1/3. Шукана ймовірність

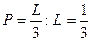Нехай плоска фігура g складає частину плоскої фігури G. На фігуру G навмання кинута точка. Це означає виконання наступних припущень: кинута точка може виявитися в будь-якій точці фігури G, ймовірність попадання кинутої точки на фігуру g пропорційна площі цієї фігури і не залежить ні від її розташування відносно G, ні від форми g. У цих припущеннях ймовірність попадання точки у фігуру g визначається рівністю

Приклад 2. На площині накреслені два концентричні кола, радіуси яких 5 і 10 см відповідно. Знайти ймовірність того, що точка, кинута навмання у великий круг, потрапить у кільце, утворене побудованими колами. Передбачається, що ймовірність попадання точки в плоску фігуру пропорційна площі цієї фігури і не залежить від її розташування відносно великого круга.

Рішення. Площа кільця (фігури g)

Площа великого круга (фігури G)

Шукана ймовірність

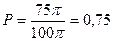Приклад 3. У сигналізатор надходять сигнали від двох пристроїв, причому надходження кожного із сигналів рівноможливе в будь-який момент проміжку часу тривалістю Т. Моменти надходження сигналів незалежні один від одн ого. Сигналізатор спрацьовує, якщо різниця між моментами надходження сигналів менше t (t<T). Знайти ймовірність того, що сигналізатор спрацює за час Т, якщо кожен з пристроїв пошле по одному сигналу.

Рішення. Позначимо моменти надходження сигналів першого і другого пристроїв відповідно через х і у. У силу умови задачі повинні виконуватися подвійні нерівності: , 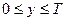. Введемо у розгляд прямокутну систему координат хОу. У цій системі подвійним нерівностям задовольняють координати будь-якої точки квадрата ОТAT (рис. 1). Таким чином, цей квадрат можна розглядати як фігуру G, координати точок якої представляють усі можливі значення моментів надходження сигналів.

Сигналізатор спрацьовує, якщо різниця між моментами надходження сигналів менше t, тобто якщо у-х < t при y > х і х-у < t при х> y, чи, що те ж саме,

y<x+t при y>x, (*)

y>x-t при y<x. (**)

Нерівність (*) виконується для тих точок фігури G, що лежать вище прямої у=х і нижче прямої y=x+t; нерівність (**) має місце для точок, розташованих нижче прямої у=х і вище прямої у=х - t.

Як видно з рис. 1, усі точки, координати яких задовольняють нерівностям (*) і (**), належать заштрихованому шестикутнику. Таким чином, цей шестикутник можна розглядати як фігуру g, координати точок якої є сприятливими моментами часу х і у.

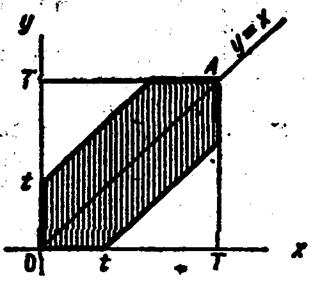
Рис. 1

Шукана ймовірність

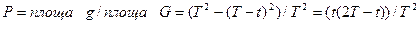Зауваження 1. Наведені визначення є окремими випадками загального визначення геометричної ймовірності. Якщо позначити міру (довжину, площу, обсяг) області через mes, то ймовірність попадання точки, кинутої навмання (у зазначеному вище змісті) в область g - частина області G, дорівнює

P=mes g/mes G.

Зауваження 2. У випадку класичного визначення ймовірність достовірної (неможливої) події дорівнює одиниці (нулю); справедливі і зворотні твердження (наприклад, якщо ймовірність події дорівнює нулю, то подія неможлива). У випадку геометричного визначення ймовірності зворотні твердження не мають місця. Наприклад, ймовірність попадання кинутої точки в одну визначену точку області G дорівнює нулю, однак ця подія може відбутися, і, отже, не є неможливою.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Обмеженість класичного визначення ймовірності. Статистична ймовірність	\|	Основні формули комбінаторики

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.