• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Короткі теоретичні відомості

Згинання з крученням (bending combined with torsion)

Надалі розглянемо лише вали круглого поперечного перерізу.

Сили, що діють на вали (тиск на зуби шестерень, натяг ременів, власна вага вала та шківів тощо), спричинюють у поперечних перерізах валів такі внутрішні силові фактори: М_кр = М_х; М_у; М_z; Q_y та Q_z. Отже, в будь-якому поперечному перерізі одночасно виникають нормальні напруження від згинання в двох площинах, а також дотичні напруження від кручення та згинання.

Для розрахунку вала насамперед треба визначити небезпечні перерізи. З цією метою слід побудувати епюри згинальних моментів М_у, М_z та крутного моменту М_х.

При згинанні вала круглого або кільцевого перерізу в кожному з його перерізів відбувається пряме згинання під дією результуючого згиналь­ного моменту (рис. 1.10)

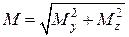. (1.10)

Положення нейтральної лінії та епюри нормальних напружень σ від результуючого згинального моменту М показані нарис. 1.11. Напруження змінюються пропорційно відстані точок від нейтральної лінії.

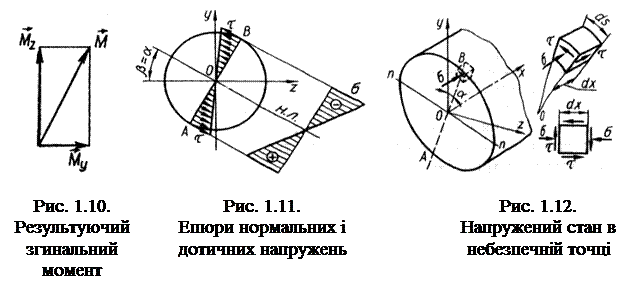
Очевидно, небезпечними точками є точки А та В, які найбільш віддалені від нейт­ральної лінії, – в них одночасно і нормальні напруження від згинання, і дотичні напруження мають найбільші значення:

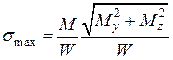; (1.11)

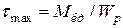. (1.12)

Біля найбільш небезпечної точки В виділимо елемент (рис. 1.12). По чотирьох його гранях діють дотичні напруження, а до двох із цих граней прикладені ще й нормальні напруження. Решта граней вільні від напру­жень. Отже, при згинанні з крученням елемент у небезпечній точці пере­буває в плоскому напруженому стані. Аналогічні напруження на гранях у брусі, що згинається.

Зазначимо, що в даному випадку складного напруженого стану впливом дотичних напружень від поперечних сил нехтуємо, оскільки вони знач­но менші, ніж дотичні напруження, спричинені крученням.

Для перевірки міцності елемента, який виділено біля небезпечної точ­ки, треба, вибравши відповідну теорію міцності, скористатися однією з формул, наприклад формулою:

за IV теорією

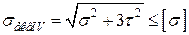. (1.13)

Підставляючи у формулу (1.13) вирази (1.11), (1.12) для напружень та враховуючи, що 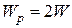,матимемо

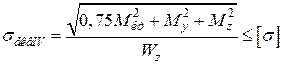. (1.14)

Чисельник цієї формули є зведеним моментом, дія якого еквівалент­на спільній дії трьох моментів (згідно з вибраною теорією міцності). Отже,

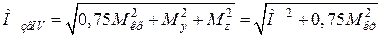. (1.15)

У разі потреби так само можна здобути формули для зведених моментів і за іншими теоріями міцності.

Неважко помітити, що тепер умову міцності (1.14) можна замінити однією простою формулою

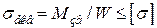. (1.16)

Отже, при спільній дії згинання з крученням стрижні круглого пере­різу розраховують на згинання від зведеного моменту М_зв.

Розв'язуючі нерівність (1.16) відносно W,дістанемо формули для визначення моменту опору:

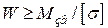(1.17)

та діаметра круглого вала:

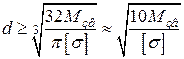. (1.18)

Зазначимо, що наведені формули цілком придатні й для стрижнів кільцевого перерізу.

Приклад. На вал (рис. 1.13) насаджені три зубчастих колеса. Колеса наванта­жені силами Р₁ = 4000Н, Р₂= 3000Н, Р₃= 2000Н, причому сила Р₁ вертикальна, а сили Р₂ та Р₃ горизонтальні. Діаметри зубчастих коліс такі: D₁ = 100 мм; D₂ = 300 мм; D₃ = 250 мм. Допустимі напру­ження [σ] = 60 МПа. Доберемо діаметр вала за IV теорією міцності.

Замінимо діюче навантаження статич­но еквівалентною системою сил.

Перенесемо сили Р₁, Р₂ та Р₃ на вісь вала, замінюючи кожну з них силою, при­кладеною в точках В, С або D відповідно, й скручувальною парою сил 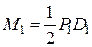; ; 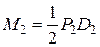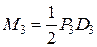відповідно. От­же, дістаємо розрахункову схему (рис. 1.13).

На схемі наведено як значення прикладе­них зовнішніх навантажень (Р_і, М_кі), так і значення спричинених ними опорних ре­акцій.

Розглядаючи окремо сили в горизонтальній та вертикальній площинах (рис. 1.14, а та б), будуємо епюри згинальних моментів. Для побудови сумарної епюри моментів М визначаємо ординати в характерних точках за формулою (1.10):

у перерізі В

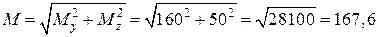Н·м;

у перерізі С

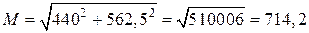Н·м;

у перерізі D

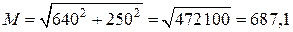Н·м.

Епюру М,побудовану за цими даними, наведено на рис. 1.14, в. Як уже зазначало­ся, на ділянках ВС та СD така епюра має завищені значення ординат (дійсні значення показано штриховою лінією).

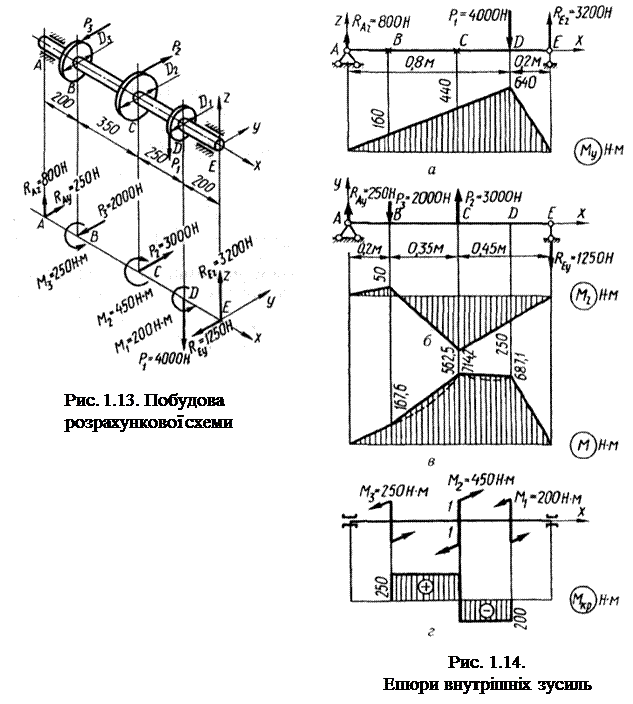
Розглядаючи моменти, що діють на вал, будуємо епюру крутних моментів (рис. 1.14, г).

Порівнюючи епюри М та М_кр, знаходимо, що небезпечним є переріз 1 – 1 ліворуч від точки С, де одночасно діють М = 714,2 Н∙м та М_кр = 250 Н∙м.

Згідно з IV теорією міцності, зведений момент визначаємо за формулою (1.15):

Н∙м.

Підставляючи зведений момент у формулу (1.17), дістаємо потрібний осьовий момент опору:

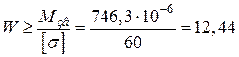см³

і, поклавши 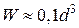, обчислюємо потрібний діаметр вала:

см.

Округливши до найближчого стандартного діаметра, вибираємо d = 50 мм.

Читайте також:

1. IX. Відомості про військовий облік
2. IX. Відомості про військовий облік
3. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
4. Активне управління інвестиційним портфелем - теоретичні основи.
5. Білковий обмін: загальні відомості
6. Біографічні відомості
7. Боротьба з проявами національної самосвідомості
8. Вальниці ковзання. Загальні відомості
9. Види правосвідомості
10. Виникнення і розвиток свідомості у людини.
11. Виникнення людської свідомості. Мова і свідомість.
12. ВІДОМОСТІ ПРО ІНФОРМАЦІЮ, КІЛЬКІСНА МІРА ЇЇ. ВИДИ ПОВІДОМЛЕНЬ

Переглядів: 834