
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Міцність при розтягуванні КМ, армованих дискретними волокнами
Критична довжина волокон.Розглянуті в пункті 1.5 формули для визначення міцності КМ справедливі лише тоді, коли армуючі волокна безперервні. Якщо ж КМ армований короткими (дискретними) волокнами, слід враховувати так званий „кінцевий ефект”, пов'язаний з концентрацією напруги у кінців волокон, який позначається на величині міцності КМ в цілому.
У КМ, армованому паралельно укладеними короткими волокнами довжиною l і навантаженому уздовж волокон, навантаження передається волокнам за рахунок дотичної напруги на поверхнях розділу між волокнами і матрицею. Залежно від довжини волокон можливі два випадки поведінки їх в КМ. При значеннях l, менших певної критичної довжини lкр, що розтягують напругу у волокнах опиняються недостатніми для того, щоб викликати їх руйнування, волокна витягуються з матриці і міцність їх недовикористання.

Рис. 1.10. Сили, що діють на волокно при розтягуванні армованої композиції
При l > lкр волокна руйнуються від розтягуючої напруги, при цьому чим більше l, тим велику міцність має КМ в цілому.
Критичною довжиною волокна lкр називають мінімальну довжину волокон, при якій вони руйнуються в КМ. Величина lкр залежить від міцності зв'язку між матрицею і волокнами і діаметру волокон. Якщо приблизно прийняти, що по довжині волокна дотична напруга розподілена рівномірно (це близько до поведінки КМ з ідеально пластичними матрицями), то значення l/lкр можна знайти з умови рівноваги дотичних і нормальних сил, що діють на волокно (рис. 1.10):
 . (1.51)
. (1.51)
Тут t – дотична напруга на межі розділу волокно – матриця;
sв – нормальна розтягуюча напруга у волокні;
l і dв – довжина і діаметр волокна.
При l = lкр у момент руйнування КМ дотична напруга рівна міцності зсуву межі розділу tг.р, а розтягуюча напруга у волокнах – їх межі міцності (sв)в. Тому
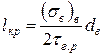 . (1.52)
. (1.52)
Таким чином, критична довжина волокон збільшується із зменшенням міцності межі розділу і збільшенням міцності волокон і їх діаметру. У КМ з пластичною матрицею максимальна дотична напруга на межі розділу може лімітуватися межею текучості матриці.
Зазвичай в розрахунках використовують безрозмірну величину, а не абсолютне значення lкр, оскільки вона не залежить від діаметру волокон. Користуючись формулою (1.52), цю величину можна оцінити по відомих (sв)в і tг.р. Розрахунок показує (табл. 1.3), що для армованих металів lкp/dв лежить в межах 10 – 250, для пластиків ця величина може дорівнювати 350 і більш.
З підвищенням температури величина tг.р зменшується, тому КМ, призначені для роботи при високих температурах, повинні мати волокна більшої довжини, чим низькотемпературні матеріали. Точне значення міцності зв'язку між арматурою і матрицею не піддається аналітичному розрахунку, тому його визначають експериментально.
Таблиця 1.3 Значення lкp/dв для КМ з різною міцністю межі розділу tг.р кгс/мм2 і трьома рівнями міцності волокон (sв)в кгс/мм2
| Матеріал матриці | tг.р | (sв)в | lкp/dв |
| Смола | 1,0 | ||
| Аl | 1,4 | ||
| Аg | 2,8 | ||
| Сu, Ni | 3,5 |
Правило сумішей для КМ з дискретними волокнами. Міцність у напрямі армування для КМ, зміцнених паралельними відрізками волокон, можна оцінити за правилом сумішей з урахуванням „кінцевого ефекту”. Розглянемо, який вплив робить довжина волокон на величину середньої розтягуючої напруги  в них.
в них.
1. l< lкр. В цьому випадку у міру збільшення довжини волокна росте як максимальна розтягуюча напруга (діє посередині волокна), так і середня розтягуюча напруга  у волокнах, яку можна розрахувати по формулі
у волокнах, яку можна розрахувати по формулі
 .
.
Припустимо, що нормальна напруга у волокнах росте від кінців волокна до його середини по лінійному закону (рис. 1.11). Тоді при l < lкр епюра напруги має вигляд, зображений на волокнах з довжинами l1 і l2. Максимальна напруга відмічена штриховою лінією, середнє – штрих-пунктирною. В цьому випадку максимальна напруга у волокнах не досягає їх межі міцності і середня нормальна напруга
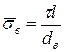 .
.

Рис. 1.11. Епюри розтягуючих напруг у волокнах різної довжини
Руйнуються такі КМ за рахунок витягування волокон. При цьому середня розтягуюча напруга у волокнах у момент руйнування КМ рівна  і рівняння аддитивності (1.41) приймає вигляд
і рівняння аддитивності (1.41) приймає вигляд
 . (1.53)
. (1.53)
Таким чином, якщо l<lкр, то міцність однонаправлених КМ зростає пропорційно об'ємній частці волокон, відношенню l/dв, міцності межі розділу і міцності матриці, залишаючись при цьому менше міцності КМ, армованих безперервними волокнами.
2. l ³ lкр Коли довжина волокна стає рівною lкр, максимальна нормальна напруга в середній частині волокна досягає значення, рівного розтягуючій напрузі sв¥ в нескінченно довгому волокні. При подальшому збільшенні l рівень максимальної напруги у волокні залишається незмінним (рівним sв¥), але збільшуються ділянки волокон, на яких діє ця напруга. Отже, росте і середня напруга, тобто для волокон завдовжки l1 < l2 < lкр < l4 має місце співвідношення 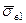 <
< 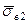 <
<  <
< 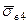
Припустимо, що величина середньої розтягуючої напруги у волокні на кінцевих ділянках завдовжки  рівна Wsв¥, де W – коефіцієнт, менший 1. Ці ділянки складають частину загальної частки волокон, рівну
рівна Wsв¥, де W – коефіцієнт, менший 1. Ці ділянки складають частину загальної частки волокон, рівну 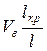 Частка ділянок, на яких діє напруга sв, складає
Частка ділянок, на яких діє напруга sв, складає 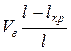 .
.
Напруга, усереднена по всій довжині волокон, можна визначити таким чином:

 . (1.54)
. (1.54)
Якщо розтягуюча напруга від кінців волокон росте лінійно (мал. 13), то W = 0,5. Тоді середня напруга у волокнах
 . (1.55)
. (1.55)
Відповідно до правила аддитивності загальна напруга, прикладена до КМ, рівна сумі середньої напруги в матриці і волокнах. Стосовно КМ з дискретними волокнами, що мають l> lкр, можна записати
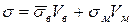 . (1.56)
. (1.56)
У момент руйнування , а
, а  . Підставивши це значення замість
. Підставивши це значення замість  в рівняння (1.56) і замінивши в нім напругу в матриці sм напругою
в рівняння (1.56) і замінивши в нім напругу в матриці sм напругою 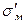 одержимо формулу для оцінки міцності КМ, армованою дискретними волокнами, яка разом з впливом об'ємної частки волокон враховує і вплив їх довжини:
одержимо формулу для оцінки міцності КМ, армованою дискретними волокнами, яка разом з впливом об'ємної частки волокон враховує і вплив їх довжини:
 . (1.57)
. (1.57)
Як і при армуванні безперервними волокнами, межа міцності композиції з короткими волокнами росте пропорційно Vв, якщо Vв > Vmin. Із збільшенням відношення l/lкр міцність КМ зростає, наближаючись до міцності композицій з безперервними волокнами (l/ lкр = ¥).
Зіставивши між собою рівняння (1.41) і (1.57) і поклавши в останньому W»0,5, одержимо співвідношення між міцностями КМ, зміцнених дискретними і безперервними волокнами:
 . (1.58)
. (1.58)
Як показують розрахунки, вже при l/lкр = 10 міцність КМ з дискретними волокнами досягає 95% міцності КМ з безперервними волокнами. Таким чином, армування дискретними волокнами дозволяє одержати практично ту ж міцність композицій, що і армування безперервними волокнами, якщо відрізки волокон достатньо довгі.
Мінімальну і критичну частку дискретних волокон в КМ розраховують так само, як і у разі КМ з безперервними волокнами. Наприклад
 . (1.59)
. (1.59)
Критична і мінімальна частка дискретних волокон завжди більша, ніж відповідні значення для безперервних волокон. Наприклад, у алюмінію, армованого волокнами з (sв)в = 70 кгс/мм2, для безперервних волокон Vкр = 8,3%, а для дискретних волокон з l/lкр = 1 частка Vкp = 17,4%.
Читайте також:
- Електрична міцність матеріалів.
- Жароміцність зварних з’єднань.
- Імпульсна міцність ізоляції
- Класифікація армованих КМ
- Міцність зв’язку Х-Х і хімічні властивості простих речовин.
- Міцність і пластичність металу
- Міцність однонаправлених КМ з безперервними волокнами у напрямі армування
- Модулі пружності однонаправлених армованих КМ
- Основи розрахунку елементів рульового керування на міцність.
- Передача інформації з дискретними і неперервними каналами зв'язку
- Перша допомога при переломах, звихненнях, ударах, розтягуванні зв'язок
| <== попередня сторінка | | | наступна сторінка ==> |
| Міцність однонаправлених КМ з безперервними волокнами у напрямі армування | | | Тема завдання: виконати дослідження фізико-механічних властивостей однонаправлених і шаруватих композиційних матеріалів (КМ). |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |